Svar på opgave 1:

1. Nedenstående graf er tegnet i Excel:

   

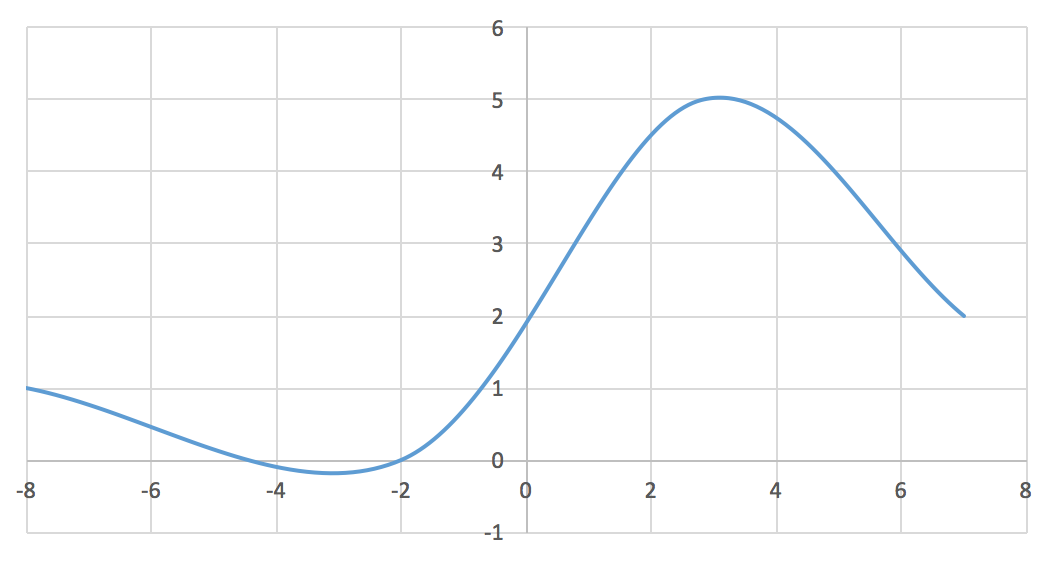
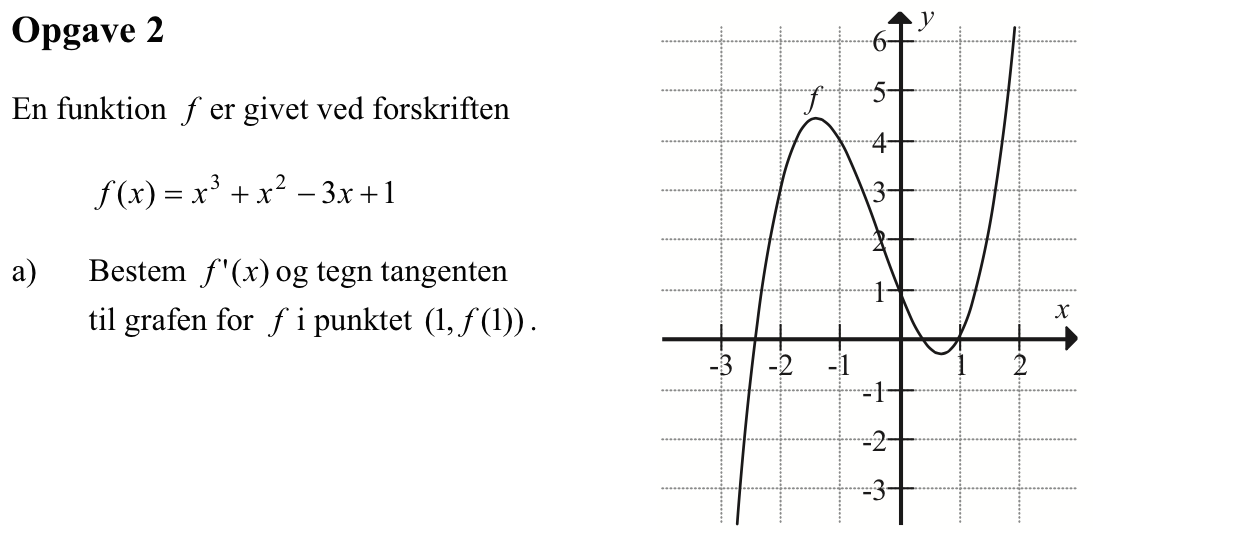
Svar på opgave 2:

1. f´(x) = 3x² + 2x - 3

   

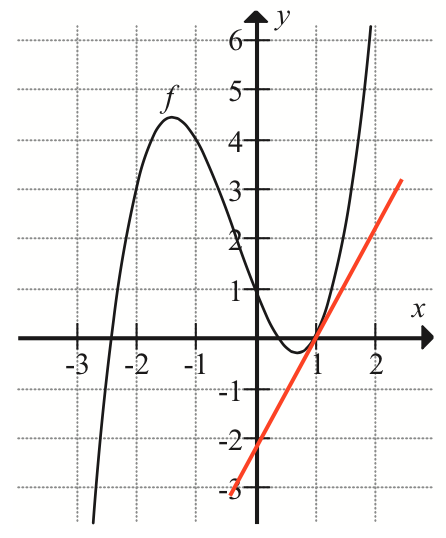
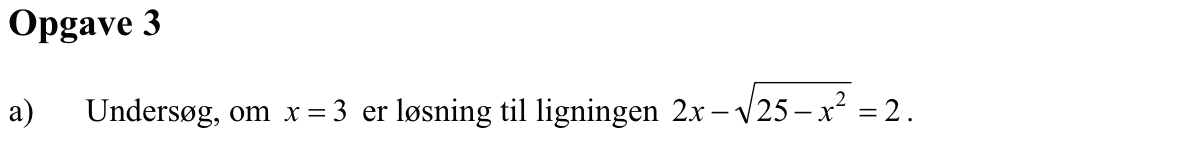
Svar på opgave 3:

1. Man skal gøre prøve ved at indsætte x = 3 i ligningen og se, om venstre og højre side giver det samme. Man får:

   Venstre side: 2·3 - √(25 - 3²) = 6 - √(16) = 6 - 4 = 2

   Højre side: 2

   Da venstre og højre side giver det samme følger, at x = 3 er en løsning til ligningen

Svar på opgave 4:

1. Man har to lineære ligninger med to ubekendte. Den ene ubekendte er x, den anden C(x). Man får:

   6000 = a·150 + b ∧ 7500 = a·200 + b ⇒

   6000 - a·150 = b ∧ 7500 = a·200 + (6000 - a·150) ⇒

   6000 - a·150 = b ∧ 7500 - 6000 = a·50 ⇒

   6000 - a·150 = b ∧ 1500/50 = a ⇒

   a = 30 ∧ b = 6000 - 30·150 ⇒

   a = 30 ∧ b = 1500

   Forskriften er C(x) = 30x + 1500 kr.

   Omkostningerne ved en produktion på 400 er C(400). Det findes til:

   C(400) = (30·400 + 1500) kr. = (12000 + 1500) kr. = 13500 kr.

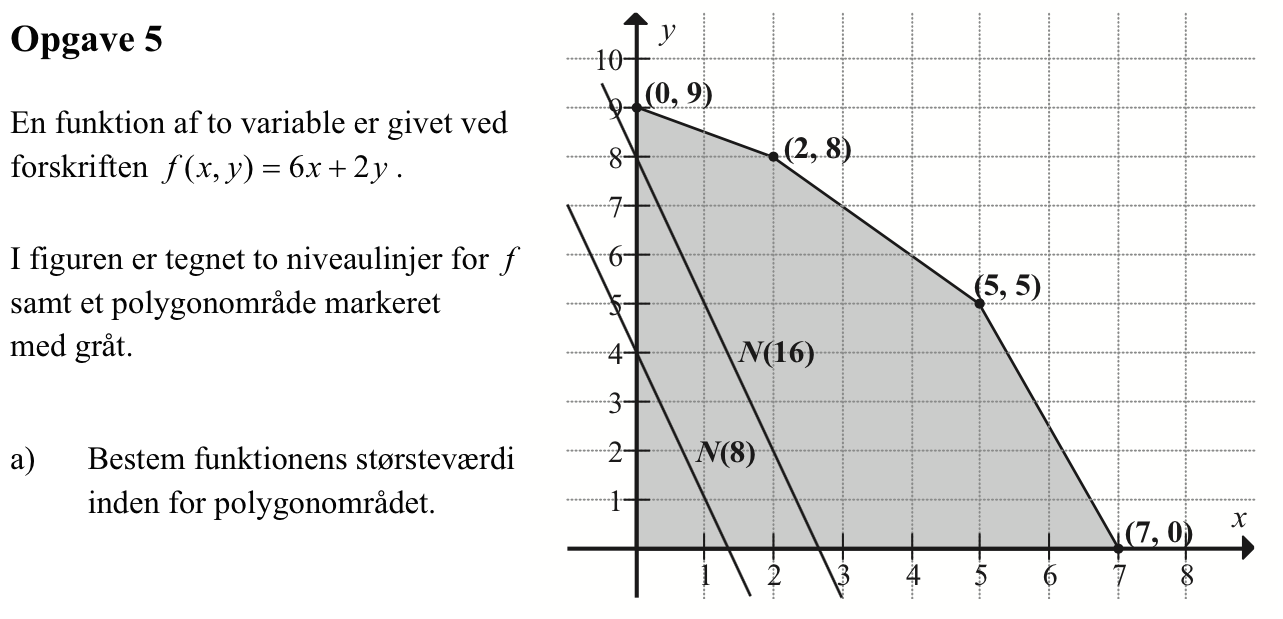
Svar på opgave 5:

1. For at finde maksimum for f(x,y) i polygonområde, parallelforskyder man linjen N(16) så langt væk fra (0,0) den kan komme uden at gå uden for polygonområdet.

   

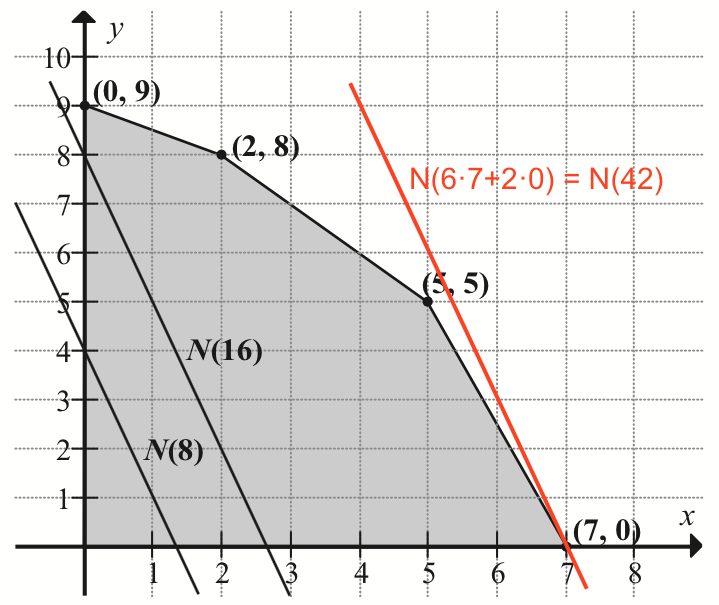
   Denne linje (tegnet med rød) går gennem punktet (7,0). Man indsætter x = 7 og y = 0 i f(x,y) og får: f(7,0) = 6·7 + 2·0 = 42.

   Dvs. største værdien af f inden for polygonområdet er 42

Svar på opgave 6:

1. Man isolerer a ved hjælp af solve-kommandoen i Ti-Nspire:

   solve(t=ln(2)/ln(a),a) ▸ a=2^1/t

   Dvs. a = 2^1/t

2. Man får:

   

Svar på opgave 7:

1. Nedenfor er vist en sumkurve for den daglige afsætning lavet i Excel. Intervallerne, der er valgt for afsætningen i kr., er: 0-5000, 5000-10000, 10000-15000, 15000-20000, 20000-25000, 25000-30000.

   

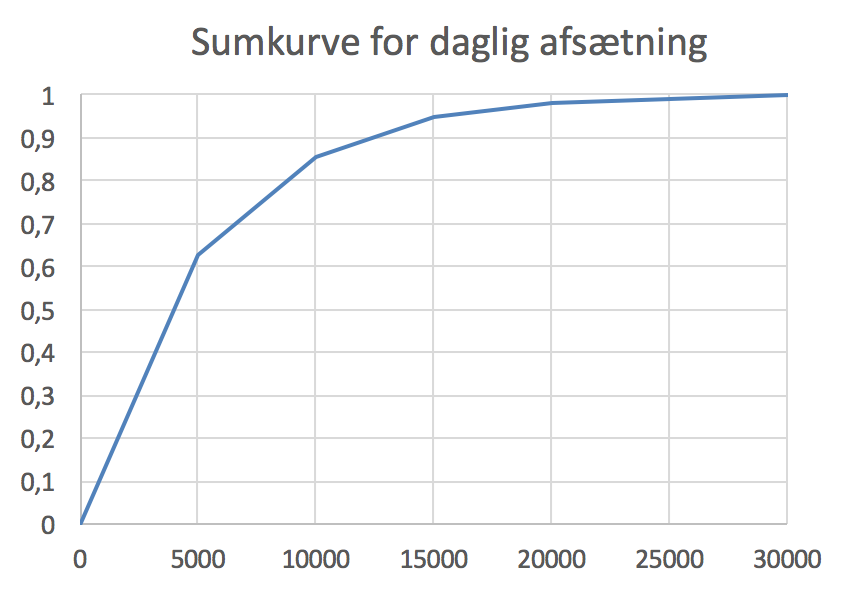
2. Gennemsnit, median og 25%-kvartilen findes i Excel ud fra afsætningstallene i kolonne B i Excel-filen. De formler der brugt er vist under tallene.

   

   Man får: gennemsnit = 5428,26 kr./dag, median = 3732,50 kr./dag og 25%-kvartilen = 2198,50 kr./dag

3. Nedenunder er vist et xy-plot af den daglige omsætning som funktion af billetsalg. Den lineære regressionsmodel (eller lineær tendenslinje) er vist med rød skrift.

   

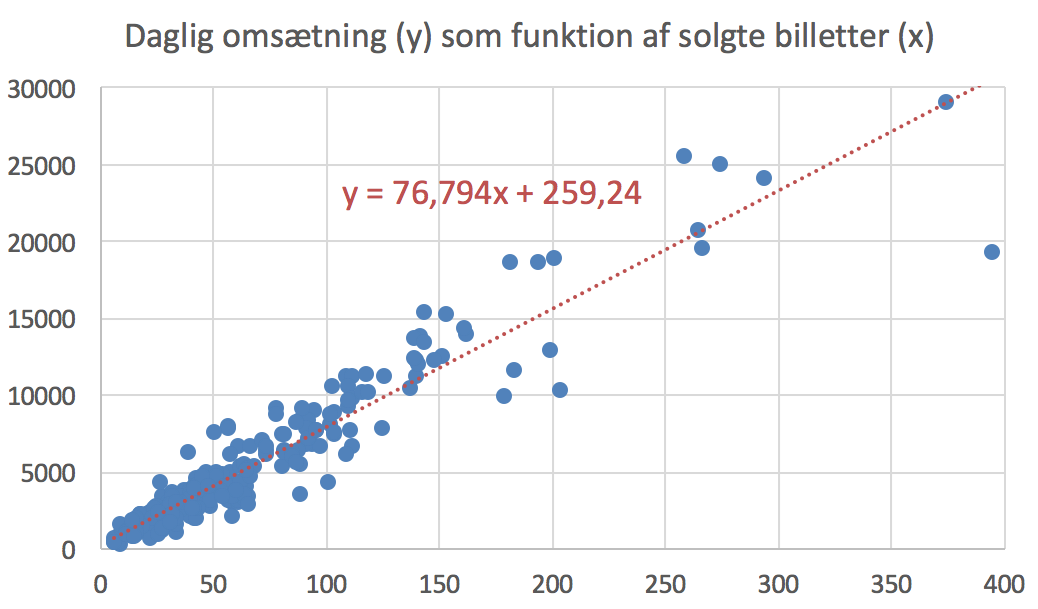
   Den lineære regressionsmodel er som vist: y = 76,794x + 259,24 kr., hvor x er billetsalg og y er omsætning.

4. Den gennemsnitlige omsætning er 5400 kr/dag. Omsætningen stiger i gennemsnit med 77 kr. pr. solgte billet.

(Se også Excelfilen Biograf.)

Svar på opgave 8:

1. Man laver tabellen som vist neden under i Excel vedhjælp af den formel, som er vist nederst på rød baggrund.

   

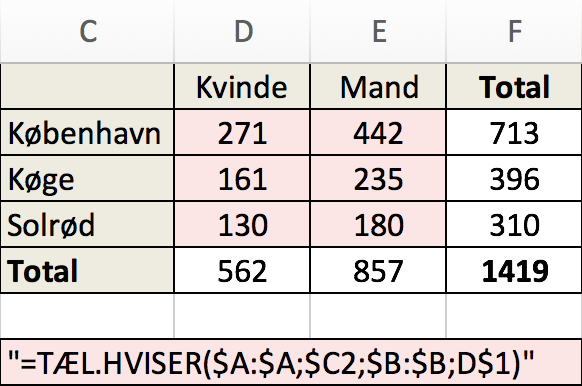
2. Nulhypotesen er, at valg af fitnesscenter et sted i landet ikke afhænger af køn. En alternativ hypotese er, at valg af fittnesscenter afhænger af køn.

3. Man laver en tabel af forventede værdier ud fra den første tabel som kaldes "Observerede". Forventede værdier beregnes som produktet af række-total og kolonne-total divideret med det samlde antal observationen ud fra tabellen "Observeret".

   

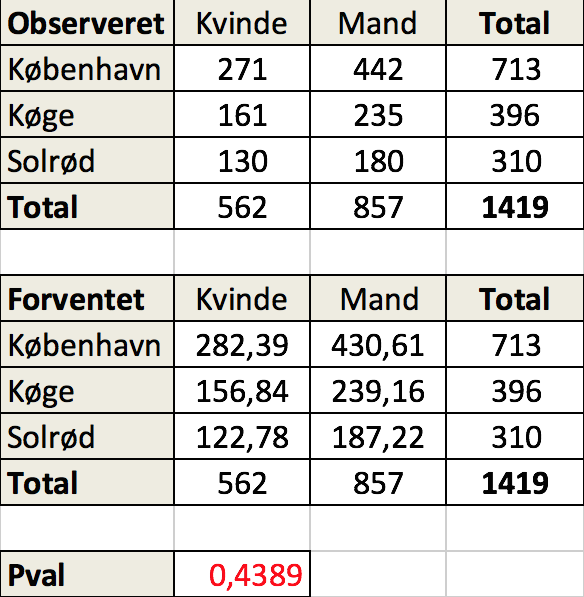
   Der laves en chi-i-anden test på de to tabeller som giver resultatet 0,4389, der er sandsynligheden for at afvigelsen mellem observerede og forventede værdier kan skyldes tilfældighed. Da dette tal er større end 5% accepteres nulhypotesen

(Se også Excelfilen Fittnessdk.)

Svar på opgave 9:

1. Man undersøger det hele:

   Nulpunkter findes i Ti-Nspire ved hjælp af solve-kommandoen, der anvendes på ligningen f(x) = 0:

   solve(f(x)=0,x) ▸ x=−71.632 or x=48.333 or x=173.30

   Fortegnsvariation findes i Ti-Nspire ved hjælp af solve-kommandoen, der anvendes på ligningerne f(x) < 0 og f(x) > 0:

   solve(f(x)<0,x) ▸ 48.333<x<173.30 or x<−71.632

   solve(f(x)>0,x) ▸ −71.632<x<48.333 or x>173.30

   Monotoniforhold findes i Ti-Nspire ved hjælp af solve-kommandoen, der anvendes på ligningerne f´(x) < 0 og f´(x) > 0:

   solve(derivative(f(x),x)<0,x) ▸ −20.711<x<120.711

   solve(derivative(f(x),x)>0,x) ▸ x>−20.711 or x>120.711

   Ekstremumspunkter findes med kommandoen:

   solve(derivative(f(x),x)=0,x) ▸ x=−20.711 or x=120.71

   Det giver:

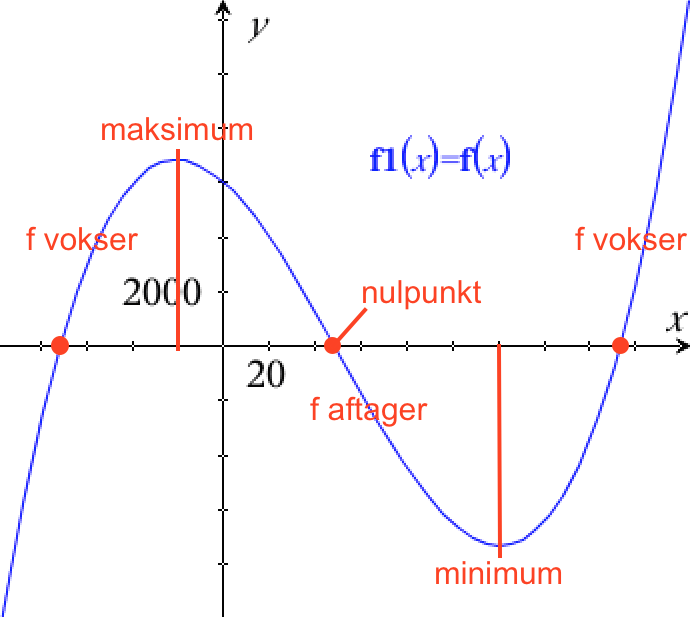
   Nulpunkterne er x = −71,632 ∨ x = 48,333 ∨ x = 173,30

   Fortegnsvariationen er : f(x) er negativ for 48.333 < x < 173.30 eller x<−71.632,

   ...f(x) er positiv for −71.632 < x < 48.333 eller x > 173.30

   Monotoniforholdene er : f(x) aftager for −20.711 < x < 120.711

   ...f(x) vokser for x < −20,711 eller x > 120,71

   Ekstremumspunkterne er x = −20,711 eller x = 120,71,

   ...idet det samtidig bemærkes, at f´(x) skifter fortegn, når hver af disse x-værdier passeres.

   Da f´(x) går fra positiv til negativ ved x = −20,711, er dette et lokalt maksimum. Da f´(x) går fra positiv til negativ ved x = 120,71, er dette et lokalt miniimum.

2. Graf for f i Ti-Nspire:

   

Svar på opgave 10a:

1. S(x) oprettes i Ti-Nspire:

   s(x):=360*x+1000 ▸ Udført

   Prisen ved en udbudt mængde på 4,8 tons findes som S(4,8) i Ti-Nspire

   s(4.8) ▸ 2728.

   Dvs. prisen er 2728 kr.

   Den udbudte mængde i tons ved en pris på 2800 kr. findes ved hjælp af solve-kommandoen i Ti-Nspire

   solve(s(x)=2800,x) ▸ x=5

   Dvs. udbuddet er 5 tons

2. Man opretter d(x) i Ti-Nspire:

   d(x):=−x³+75*x²-1875*x+16000 ▸ Udført

   Man skal finde det x, hvor s(x) = d(x) (ligevægtsmængden). Den findes i Ti-Nspire:

   solve(s(x)=d(x),x)|1≤x≤20 ▸ x=9.2066

   Dvs. ligevægtsmængden er 9,21 tons

   Ligevægtsprisen er s(9.2066) = 4314 kr.

Svar på opgave 10b:

1. For at finde a og b skal man løse to ligninger med to ubekendte. Det gøre i Ti-Nspire:

   solve(1017594=b*4^a and 2080341.=b*9^a,a,b) ▸ a=0.8818 and b=299688

   Dvs. m(x) = 299688·x^0,882

2. Man skal løse ligningen m(x) = 2500000 med hensyn til x, idet det bemærkes at m(x) er voksende, da a > 0 og at m(x) derfor vil være større end 2500000 for x større end løsningen til ligningen.

   Løsningen findes i Ti-Nspire ved først at oprette m(x) og dernæst bruge solve-kommandoen:

   m(x):=299688*x^0.8818 ▸ x=11.086

   Dvs. antallet af bredbåndsabonnementer overstiger 2 500 000 efter 11 år eller i 2011

Svar på opgave 10c:

1. Man bruger gældsformlen A₀ = y·(1−(1+r)⁻ⁿ)/r, hvor man skal fidne rentesatsen r. Man får ligningen

   25000 = 728·(1−(1+r)⁻⁶⁰)/r. Den løses i Ti-Nspire med solve-kommandoen:

   solve(25000=728*(1-(1+r)^-60)/r,r)|r>0 ▸ r=0.0205

   Dvs. renten er 0,0205 eller 2,5 %

2. Den effektive årlige rente, i, for en månedlig rentetilskrivning på r følger formlen: i = (1+r)ⁿ –1. Her er r = 2,05% eller 0,0205 og man får dermed:

   den effektive årlige rente er 1,0205¹² - 1 = 0,276 = 27,6 %