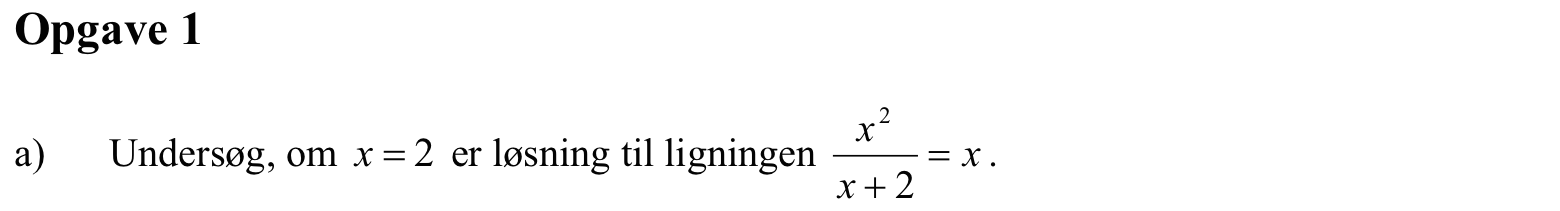
Svar på opgave 1:

1. Man skal gøre prøve ved at indsætte x = 2 i ligningen for at se om, venstre og højre side giver det samme. Man får:

   Venstre side: 2²/(2 + 2) = 1

   Højre side: 2

   Da venstre side og højre side ikke er ens, så er x = 2 ikke en løsning til ligningen.

Svar på opgave 2:

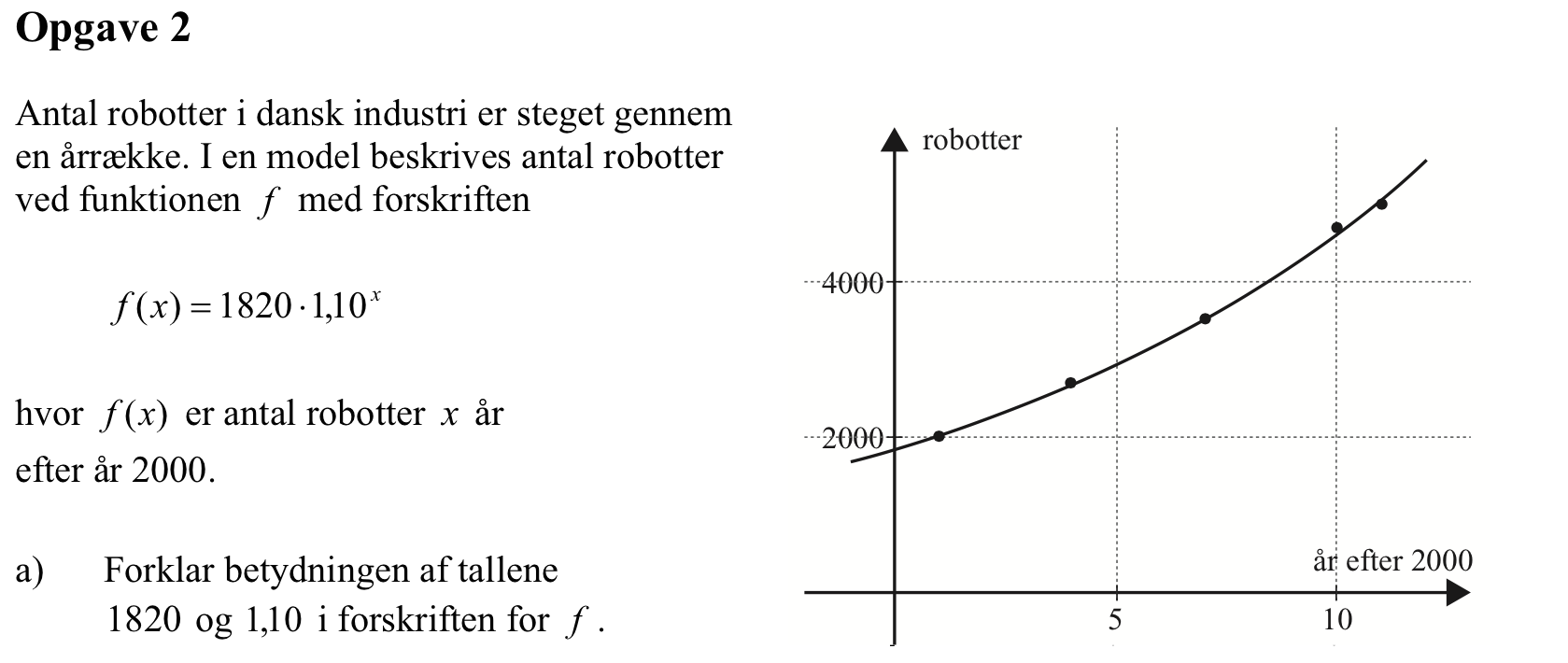
1. Tallet 1820 er startværdien, dvs. antallet af robotter år 2000.

   Tallet 1,10 er fremskrivningsfaktoren, dvs. den faktor man ganger det sidste års tal med for at få det nye års.

Svar på opgave 3:

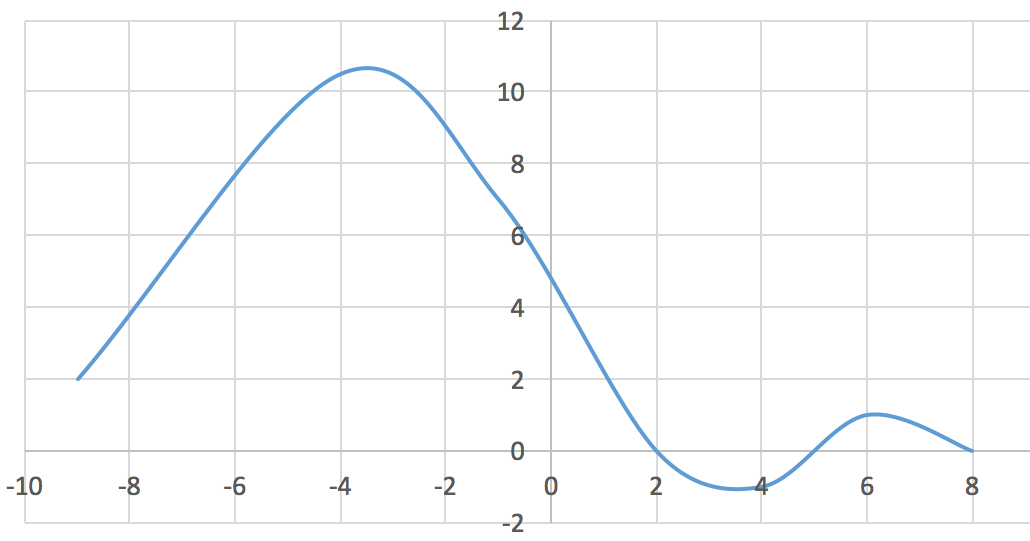
1. Nedenstående graf er lavet i Excel:

   

Svar på opgave 4:

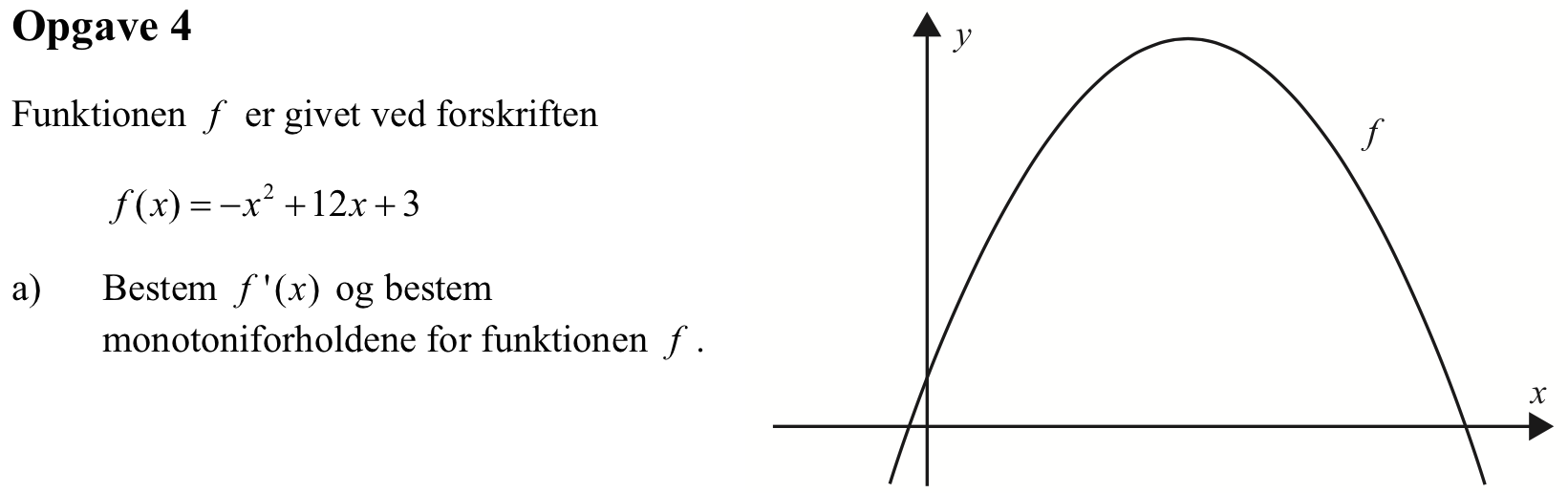
1. Funktionen f er en parabel, som vender grenene nedad. Den er voksende indtil x-værdien af toppunktet og derefter aftagende.

   Man finder x-værdien af toppunktet ved at differentiere f og sætte differerentialkvotienten lig med 0.

   Man får: f´(x) = -2x + 12. Dette giver følgende x-værdi af toppunktet: f´(x) = 0 ⇒ -2x + 12 = 0 ⇔ x = 6.

   Dvs. monotoniforholdene er: f er voksende for x < 6 og f er aftagende for x > 6

Svar på opgave 5:

1. Man skal løse ligningerne p(1000) = 500 og p(750) = 1000 med hensyn til a og b.

   p(1000) = 500 ∧ p(750) = 1000 ⇒

   a·1000 + b = 500 ∧ a·750 + b = 1000 ⇒

   a = (500 - b)/1000 ∧ ((500 - b)/1000)·750 + b = 1000 ⇒

   a = (500 - b)/1000 ∧ 0,25·b = 625 ⇒

   a = (500 - 2500)/1000 ∧ b = 2500 ⇒

   a = -2000/1000 ∧ b = 2500 ⇒

   a = -2 ∧ b = 2500

   Dvs. p(x) = -2x + 2500

   Man finder prisen ved en afsætning på 500 stk: p(500) = -2·500 + 2500 kr. = 1500 kr.

Svar på opgave 6:

1. Man reducerer udtrykket i Ti-Nspire:

   (x⁴-y⁴)/(x²-y²) ▸ x²+y²

   Dvs. det reducerede udtryk er x² + y²

2. Man får:

   

Svar på opgave 7:

1. Nedenunder er vist en trappekurve for de kummulerede frekvenser af beløbene.

   

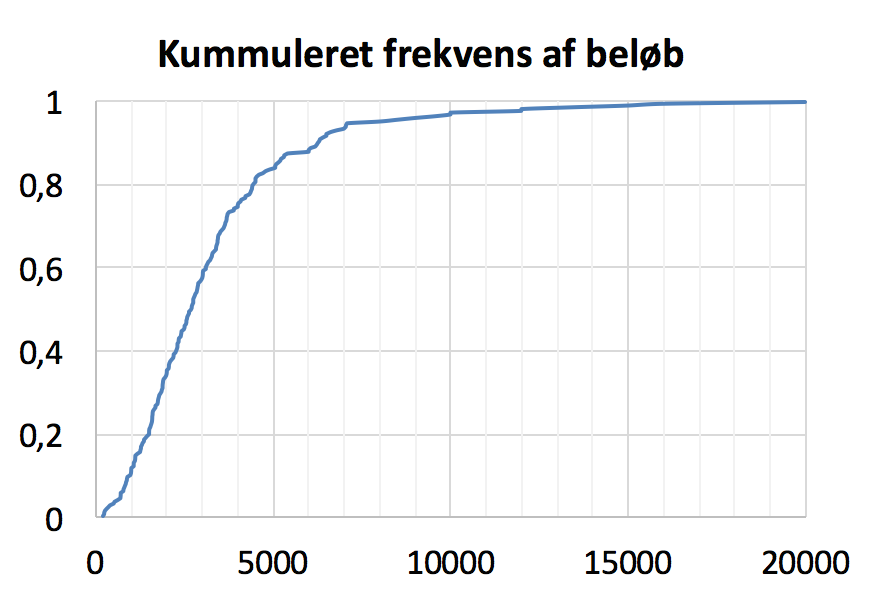
2. Typetal er det beløb som forekommer oftest. Dette er 2744, som forekommer tre gange. (Man bruger kommandoen HYPPIGST() i Excel.)

   Medianen er 2687,50 kr. Det er (med mindre flere ens beløb ligger netop på medianen) det beløb, som halvdelen af beløbene er mindre end.

   Man finder 1. kvartil i Excel = 1601,00 kr. og tredje kvartil = 3999,75 kr. Disse tal udgør sammen med medianen kvartilsættet: {1601, 2688, 4000}

   1. kvartil er det tal som 25 % af beløbene er mindre end og 3. kvartil er det tal som 75 % af beløbene er mindre end.

   Gennemsnittet eller middelværdien er 3273,25 kr.

   Varians = 7206249

   Spredning = 2684,4

   Både varians og spredning er udtryk for beløbenes gennemsnitlige afvigelse fra middelværdien. Variansen er spredningen i anden.

3. Nedenstående graf er lavet i Excel. Regeressions kurven er fundet som den lineære tendenslinje.

   

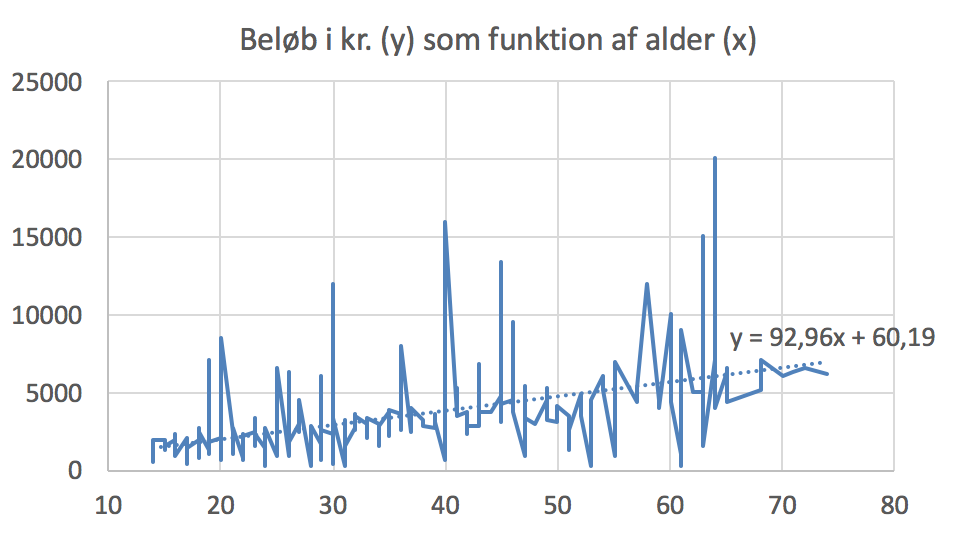
   Regressions formlen er y = 92,96x + 60,19, hvor x er alderen og y det anvendte beløb.

4. De fleste bruger beløb på ca. 3000 kr. og nedefter.

(Se også Excelfilen Elektronikkæde.)

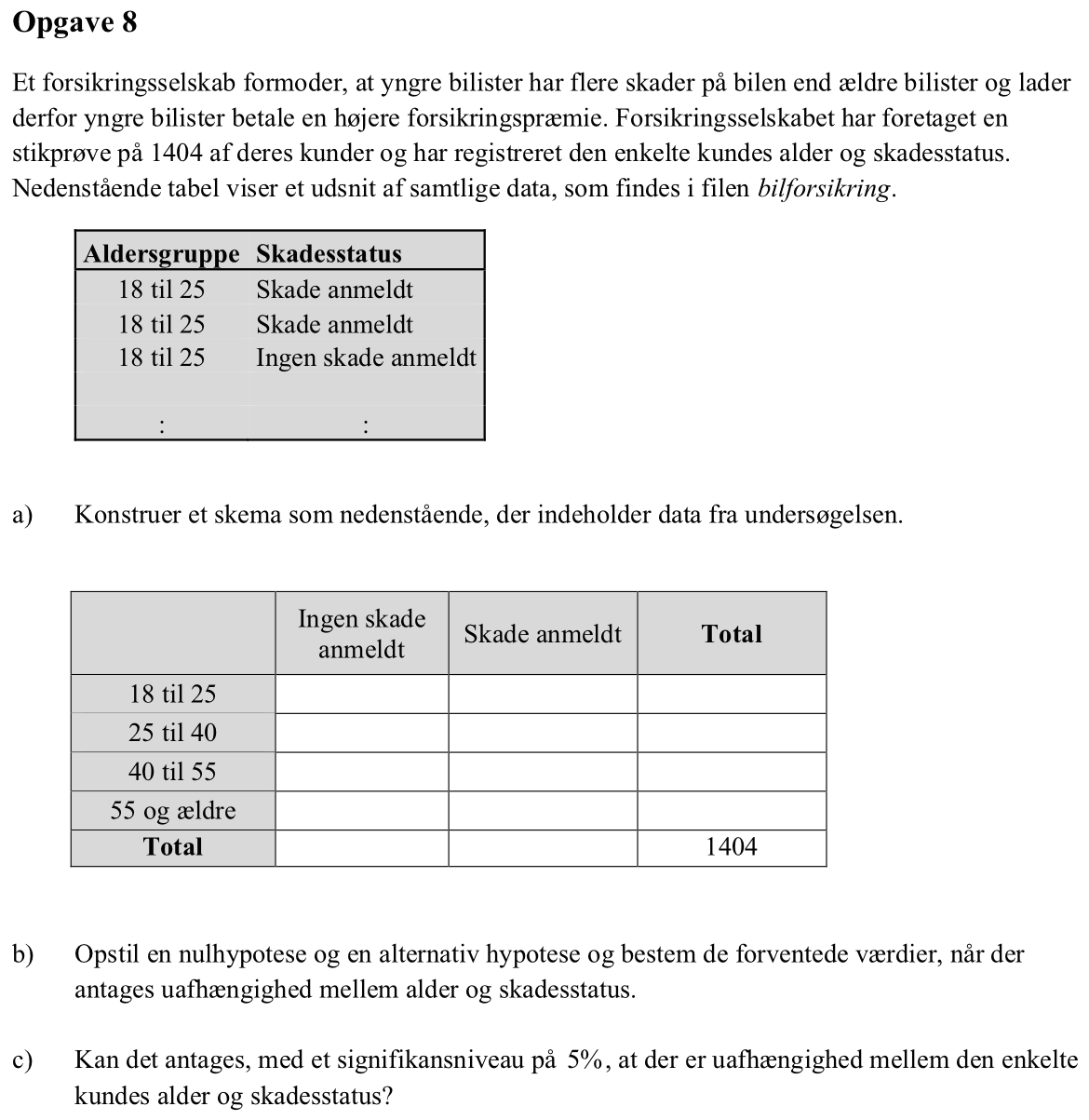
Svar på opgave 8:

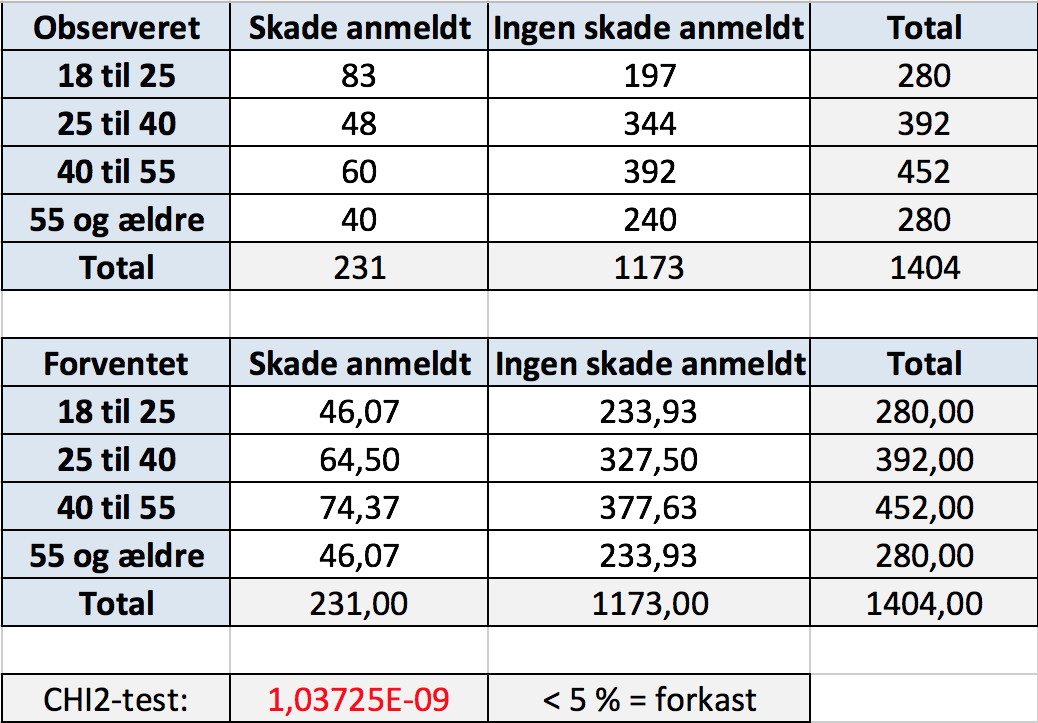
1. Nedenstående billede viser de observerede tal i øverste tabel.

   

2. Nulhypotesen er at antallet af anmeldte trafikskader er uafhængig af aldersgruppe. Den alternative hypotese er at der er en sammenhæng mellem antal skader og alder.

   Det forventede værdier er vist i den anden tabel ovenfor.

3. Neden under de to tabeller for observerede og forventede værdier på billedet ovenfor er lavet en CHI i anden uafhængighedstest i Excel. Resultatet er at P-værdien = 10^-9 som er mindre end 5 % og dermed forkastes 0-hypotesen om uafhængighed mellem alder og antal skader.

(Se også Excelfilen Bilforsikring.)

Svar på opgave 9:

1. Man opretter h(t) i Ti-Nspire:

   h(t):=0.033*t³-2.388*t²+51.31*t|0≤t≤40 ▸ Udført

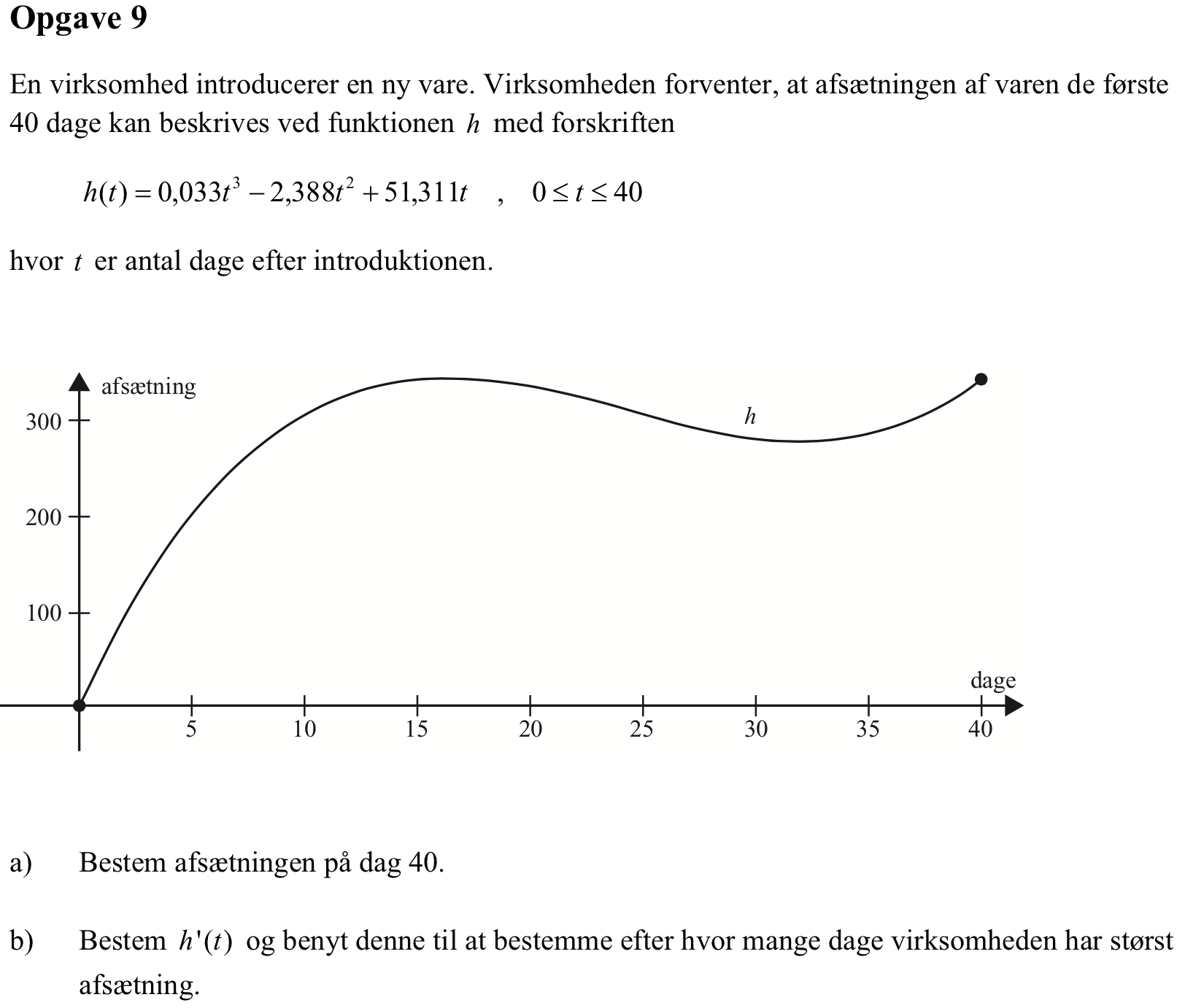
   Afsætningen efter 40 dage beregnes:

   h(40) ▸ 343.6

   Dvs. afsætningen på dag 40 er 344 stk.

2. Man beregner den afledede af h(t) med hensyn til t i Ti-Nspire:

   derivative(h(t),t) ▸ piecewise(0.099*t²-4.776*t+51.31,0.<t<40.)

   ("piecewise" kommer af, at h(t) er oprettet med et definitionsinterval.)

   Man løser ligningen h'(t) = 0 i Ti-Nspire:

   solve(derivative(h(t),t)=0,t) ▸ t=16.149384 or t=32.09304

   Maksimumspunktet må enten ligge i et af endepunkterne for funktionen eller i et ekstremumspunkt. Man indsætter det fundne værdier af t i h(t) for at se om et af dem kan være maksimum:

   h(16.1494) ▸ 344.81772

   h(32.093) ▸ 277.94519

   Det ses at h(16.1494) = 344,8 er større end h(40) = 343,6 der er det ene endepunkt. Det andet endepunkt er x = 0, hvor h(t) = 0.

   Dermed er er h(16,15) maksimum, og den masimale afsætning forekommer derfor efter 16 dage

Svar på opgave 10a:

1. Antallet af fejlfri biler følger en binomialfordeling. N = 20 og p = 0,85 (for en fejlfri bil).

   Forventingsværdien for antallet af fejlfrie biler ud af 20 er N·p = 20·0,85 = 17

2. Sandsynligheden for at højst 5 biler er fejlfrie findes i Ti-NSpire

   binomCdf(20,0.15,15,20) ▸ 3.18559E−9

   Dvs. sandsynligheden for at højst 5 biler er fejlfrie er 3,19·10^-9

Svar på opgave 10b:

1. Man bruger formlen for kapitaltilvækst over 4 terminer med en rentesats på 1 % og får:

   2000000*(1.01)⁴ ▸ 2081208.

   Dvs. lånet er vokset til 2081208 kr., som man skulle vise.

2. Den årlige ydelse beregnes ved hjælp af ydelsesformlen for annuitetsgæld:

   2081208.*(0.04)/(1-(1.04)^-10) ▸ 256594.1

   Dvs. den årlige ydelse for lånet bliver 256.594,10 kr.

Svar på opgave 10c:

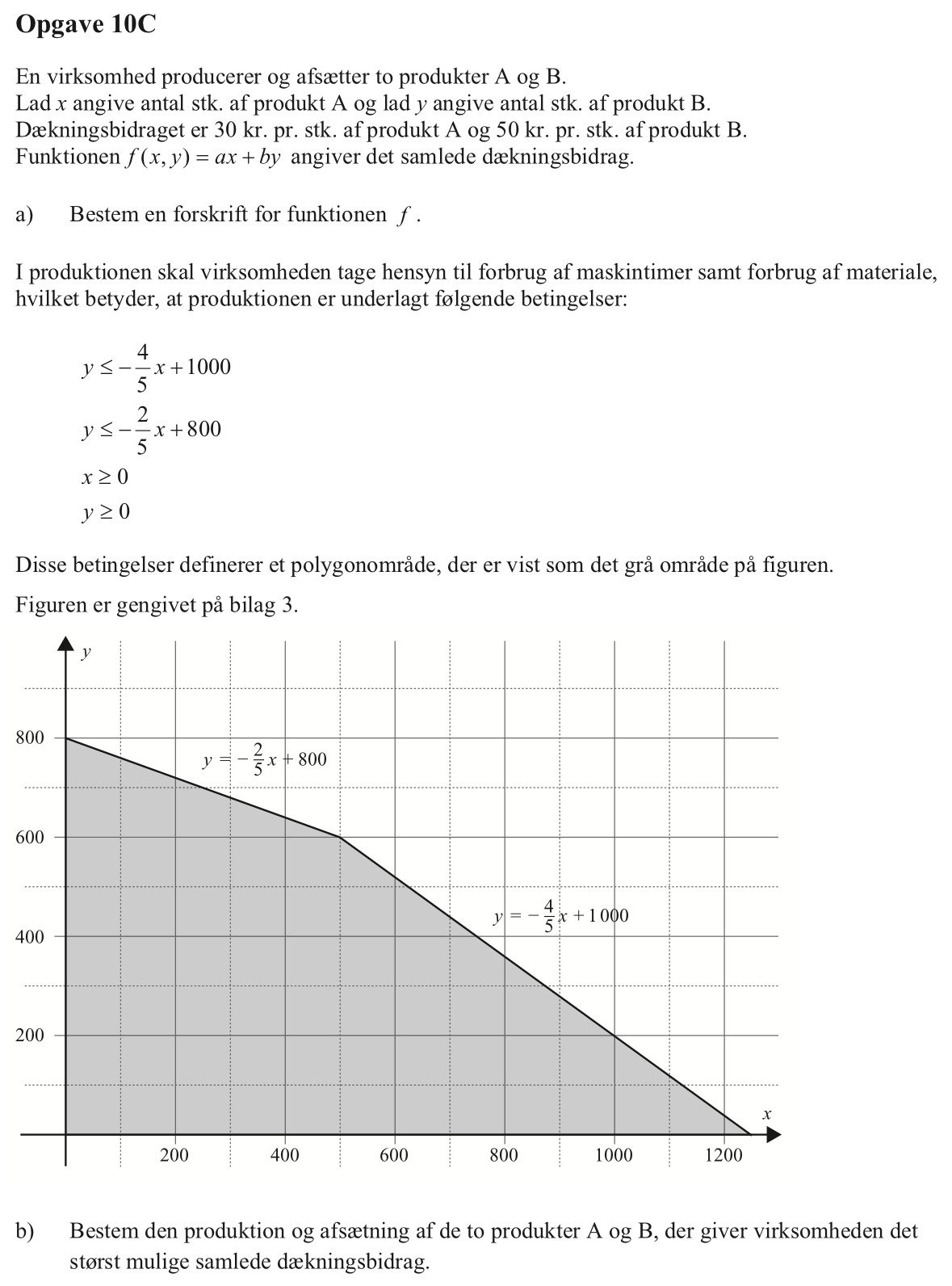
1. Forskriften for dækningsbidraget bliver f(x,y) = 30x + 50y

2. Man finder først kurven for f(x,y) = 0. Den er 30x + 50y = 0 ⇒ y = −0,6·x

   

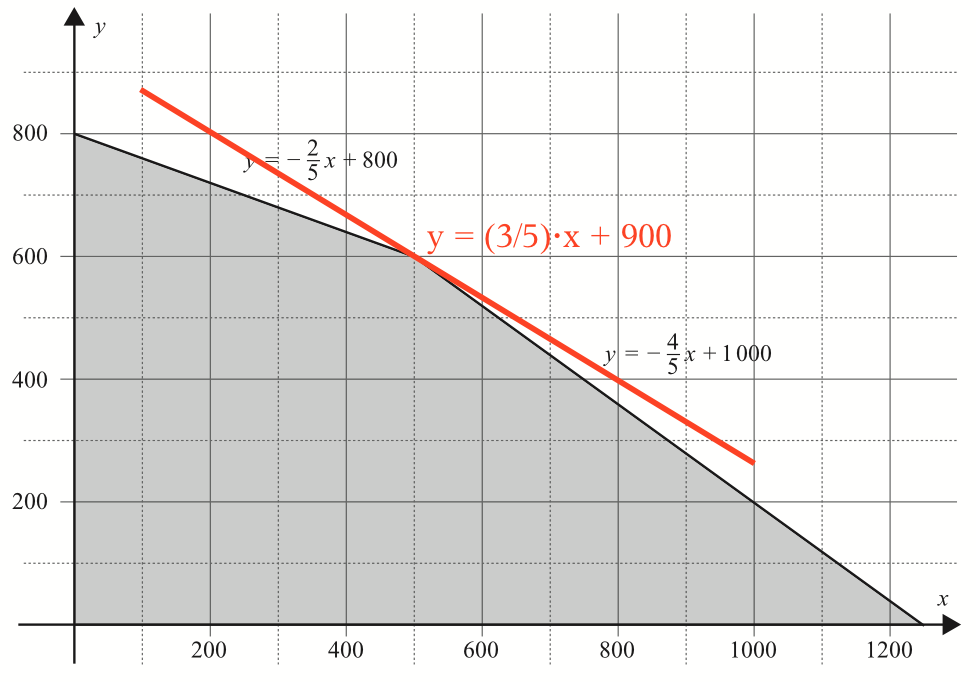
   Denne linje parallelforskydes så den netop rører afgrænsningspolygonet. Dette sker som vist i punktet (x,y) = (500,600), dvs. når salget af A = 500 stk. og salget af B = 600 stk.

   I dette optimumspunkt er dækningsbidraget: f(500,600) = 30·500 + 50·600 kr. = 45000 kr.