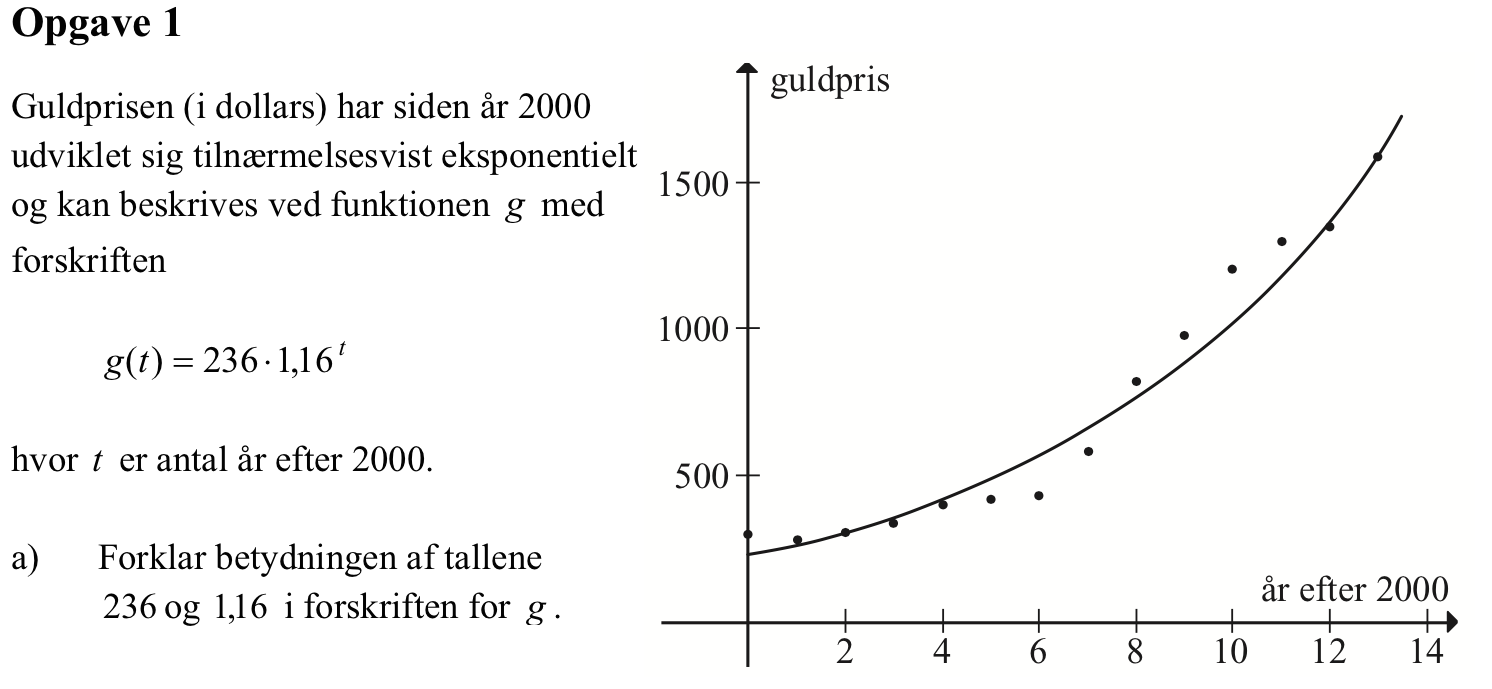
Matematik A HHX eksamen 16. august 2013 | Oversigt

Svar på opgave 1:

  1. 236 er prisen i $ i år 2000. 1,16 er fremskrivningsfaktoren, dvs. det tal man skal gange sidste års tal med for få nuværende års tal.

Svar på opgave 2:

  1. Man skal undersøge om f´(x)/[3·f(x)] er lig med x. Man får

    f(x) = x3, f´(x) = 3·x2. Dvs.

    f´(x)/[3·f(x)] = 3·x2/[3·x3] = 1/x, hvilket ikke er lig med x.

    Dette viser, at f(x) ikke er løsning til differentialligningen.

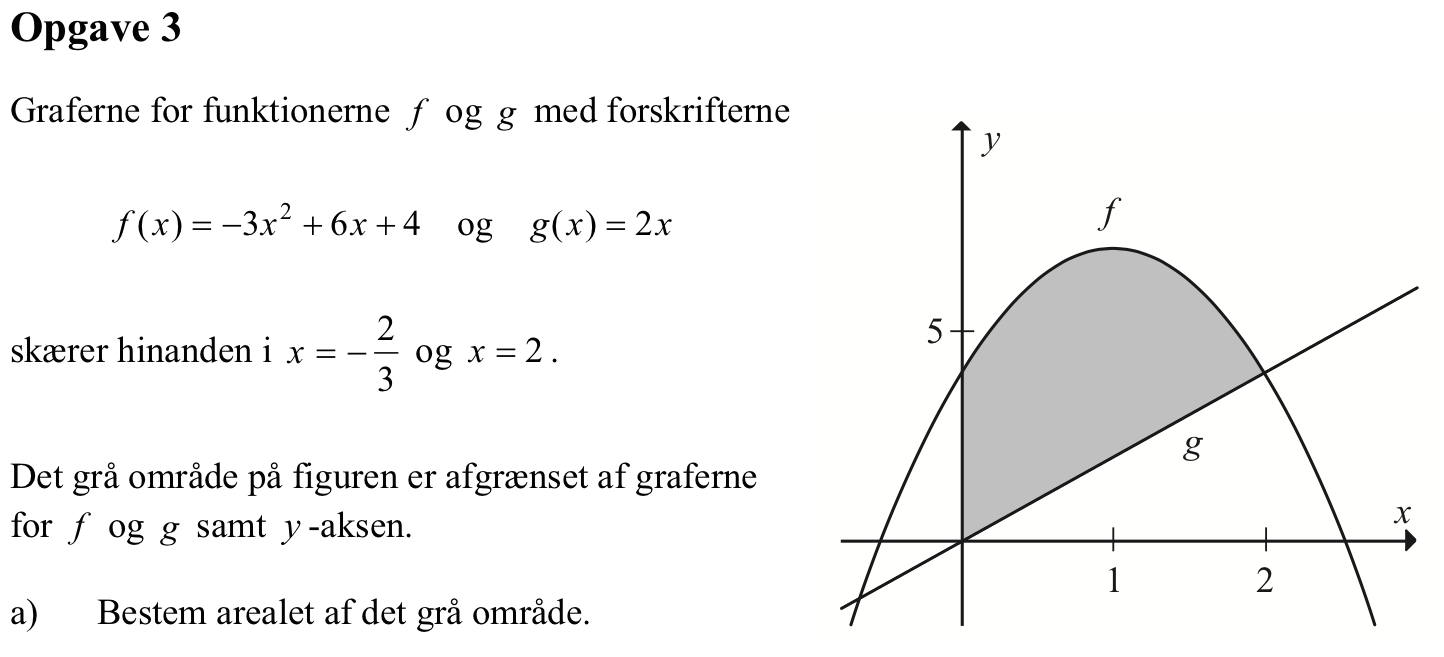
Svar på opgave 3:

  1. Arealet findes ved at integrere som vist:

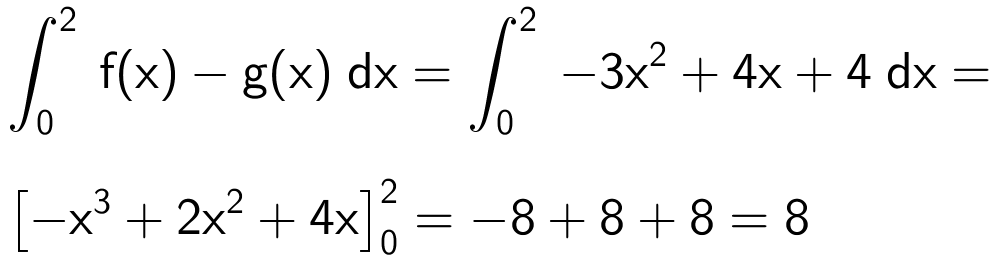
    Dvs. arealet af det grå område er 8

Svar på opgave 4:

  1. Nedenstående graf er en løsning.

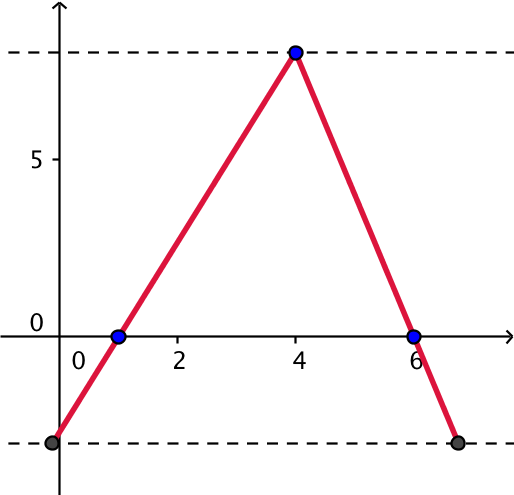
    Bemærk, der står ikke at f er differentiabel eller at f´(x) = 0 i maksimummet.

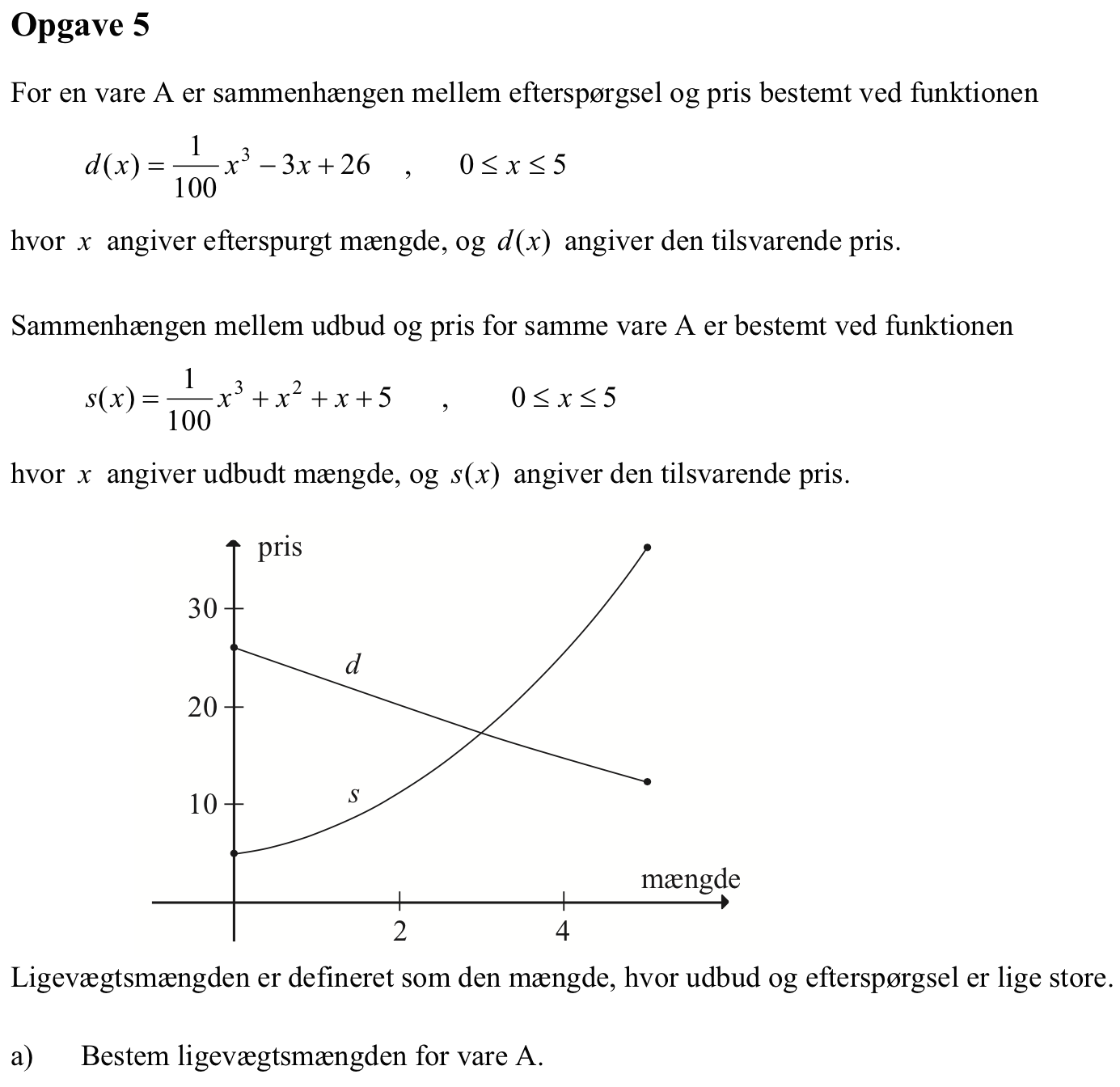
Svar på opgave 5:

  1. Man skal løse ligningen d(x) = s(x) med hensyn til x for 0 ≤ x ≤ 5. Man får:

    (1/100)·x3 - 3x + 26 = (1/100)·x3 + x2 + x + 5 ⇒

    -3x + 26 = x2 + x + 5 ⇒

    x2 + 4x - 21 = 0 ⇒

    x - 4x + 21 = 0 ⇒

    x = -7 ∨ x = 3.

    Idet 0 ≤ x ≤ 5, giver det ligevægtsmængden: 3

Svar på opgave 6:

  1. Man bruger følgende Ti-Nspire-kommandoer:

    f(x):=a*x+b ▸ Udført

    g(x):=c*x+d ▸ Udført

    solve(f(x)=g(x),x) ▸ x=(−(b-d))/(a-c)

    Dvs. løsningen er x = (d - b)/(a - c)

  2. 2) Man deler produktet op efter nulreglen og finder nulpunkter for hver faktor

    3) Man forenkler ligningerne, der kommer ud af nulreglen. Den første ligning er en andengradsligning. For den anden gælder: ln(y) = 0, hvilket kræver at y = 1. Dermed får man den sidste ligning omskrevet til en førstegradsligning.

    4) Man løser andengradsligningen og får x = -2 og x = 2. Førstegrafsligningen giver x = 7/3.

    5) Da der kræves, at 3x - 6 > 0 dvs x > 2, for at ln() til tallet er defineret, bliver løsningen: 7/3.

Svar på opgave 7:

  1. Nedenstående graf viser de kummulerede frekvenser for mælkeindvejning i Excel. Fritidshusene er inddelt i 15 lige store grupper efter pris.

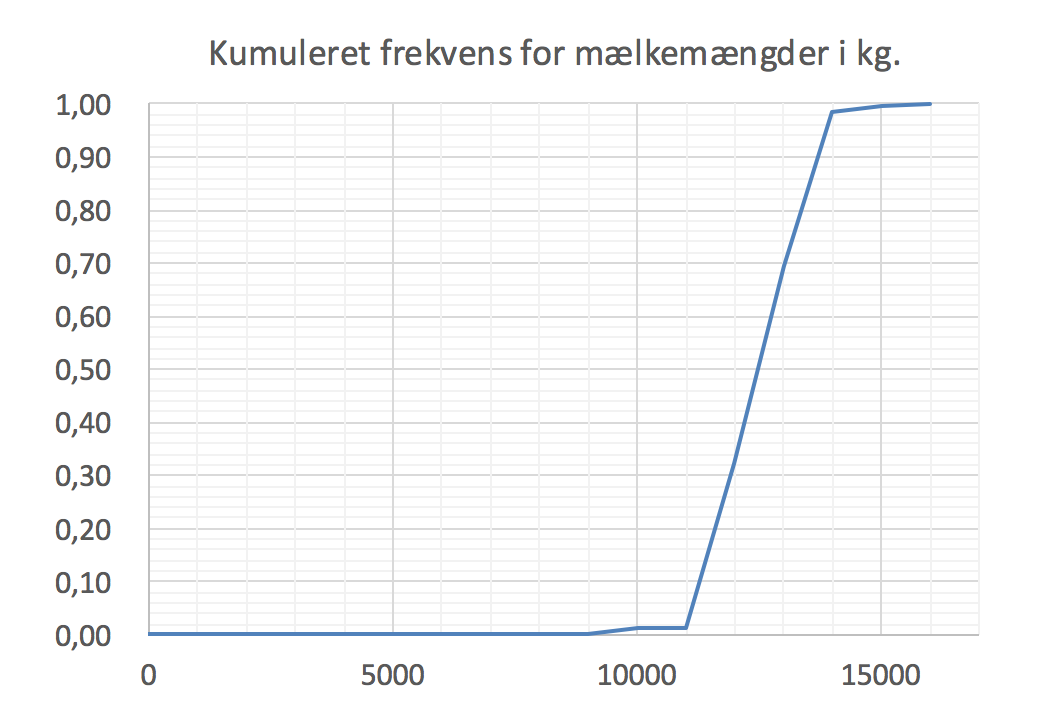
  2. I Excel finder man:

    Middel = 12884,5

    Median = 12419,0

    Standardafvigelse = 836,7

    Man skal bruge programmet Dataanalyse. I Excel 2016 installeres programmet ved at gå ind i Funktioner > Excel tilføjelsesprogrammer... og sætte hak i Analysis ToolPak og trykke OK.

    Derefter går man ind under Data > Dataanalyse > Descriptive Statistics. Dette er vist nedenfor:

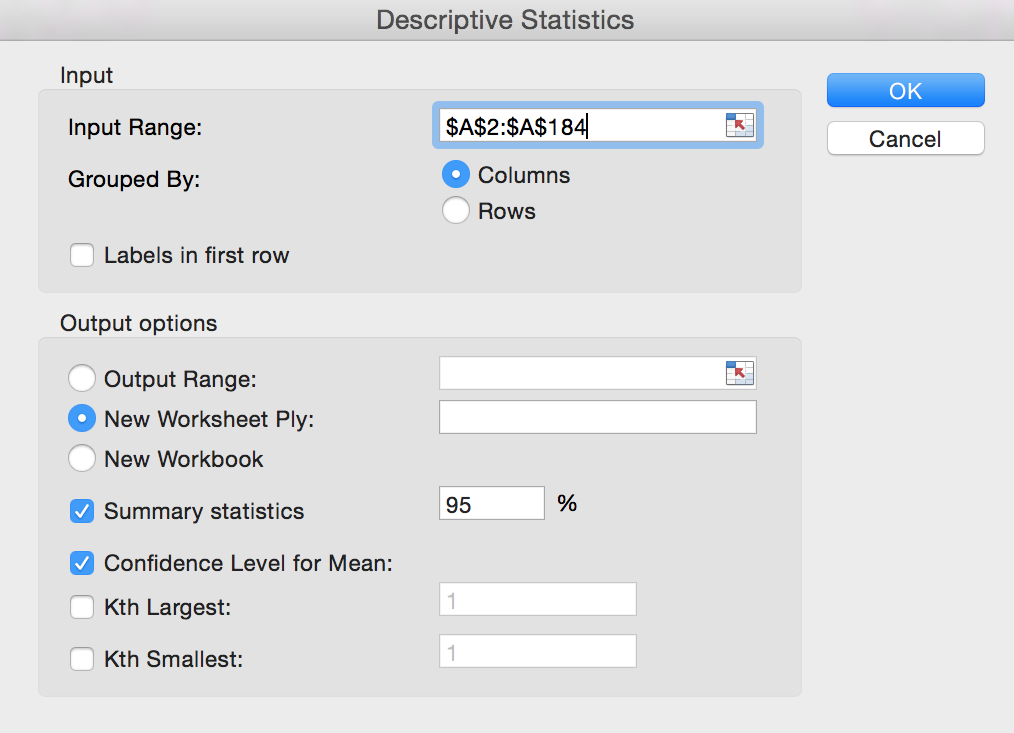
    Man får nedenstående resultat på et nyt regneark:

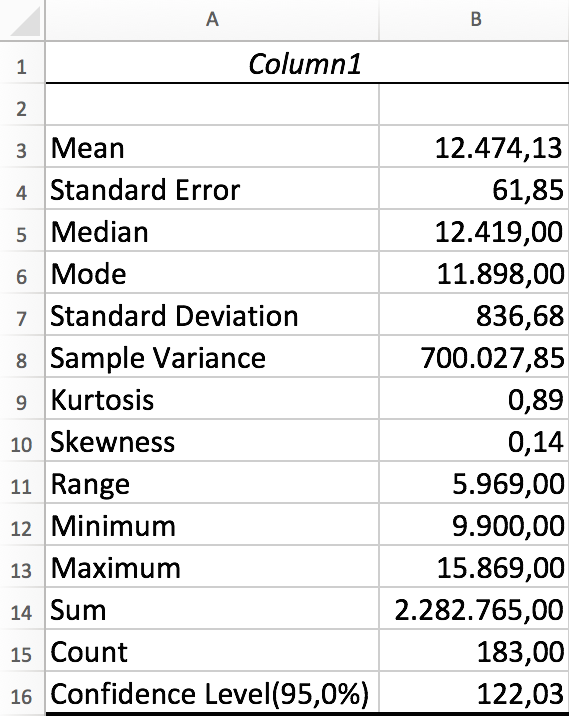
  3. For at finde konfidensintervallet bruger man "Confidence-Level(95,0%)" = 122.

    Grænserne for intervallet er: 12474,13 ± 122, der giver intervallet: [12352;12596]

  4. For at finde sandsynligheden i Excel bruger man formlen: =1-NORMFORDELING(12000;12500;840;1), der giver sandsynligheden 0,724

    I Ti-Nspire finder man sandsynligheden med kommandoen: normCdf(12000,∞,12500,840), som giver det samme.

Svar på opgave 8:

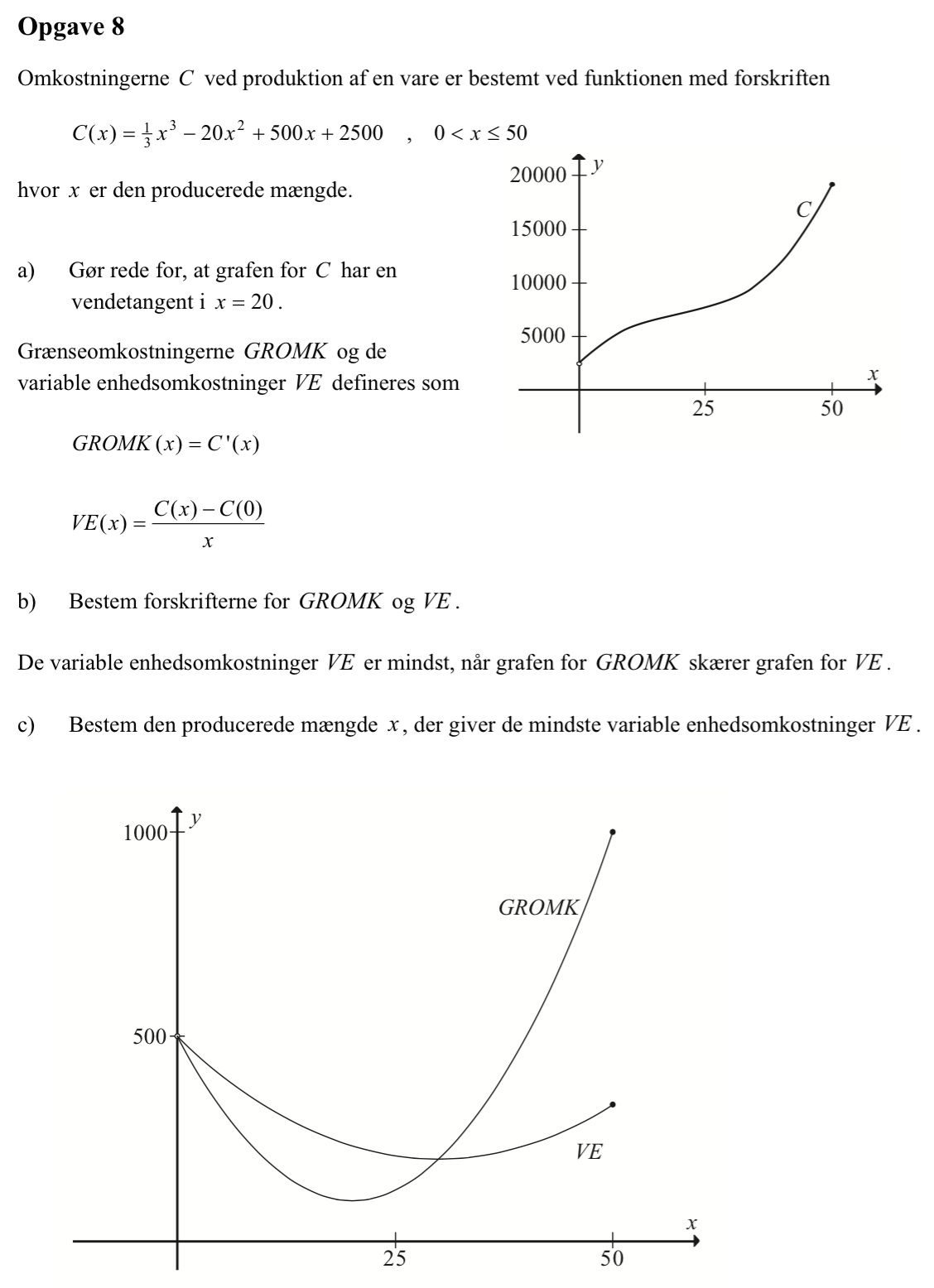
  1. C(x) har en vendetangent for x = 20, hvis C''(20) = 0.

    Man får C''(x) = 2x - 40, som giver: C''(20) = 2·20 - 40 = 0, hvilket viser, at C(x) har vendetangent i x = 20.

  2. GROMK = C'(x) = x2 - 40x + 500

    VE = [C(x) - C(0)]/x = (1/3)·x2 - 20x + 500

  3. Man skal løse ligningen: GROMK = VE med hensyn til x. Man får:

    GROMK = VE ⇒ x2 - 40x + 500 = (1/3)·x2 - 20x + 500 ⇒

    x2 - 40x = (1/3)·x2 - 20x ⇒

    (2/3)·x2 - 20x = 0 ⇒

    x2 - 30x = 0 ⇒

    x = 0 ∨ x = 30

    Dvs. den producerede mængde, der giver de mindste variable enhedsomkostninger er 30


Svar på opgave 9:

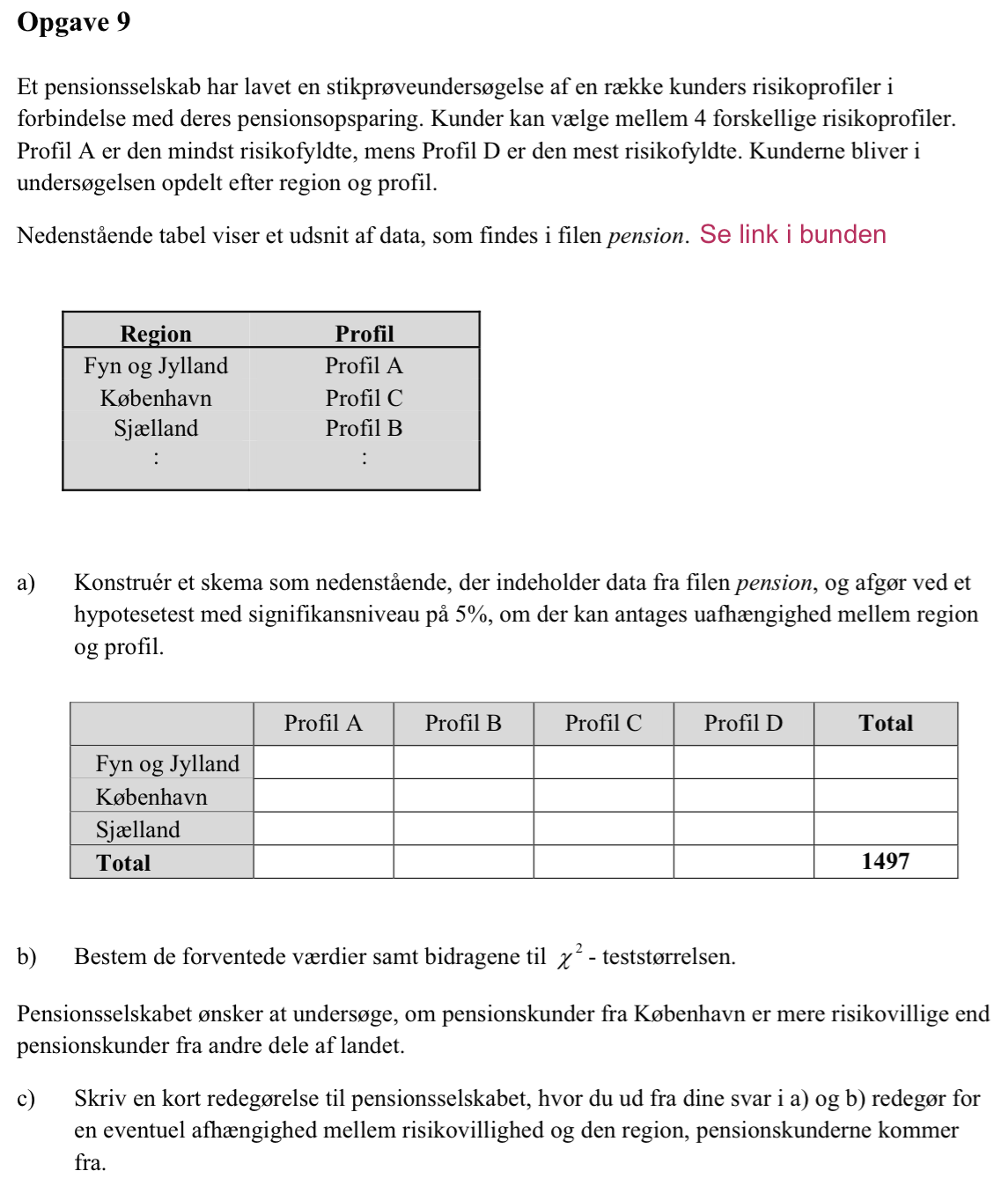
    Nedenstående billede viser både a) og b) besvaret i Excel.

  1. De sammentalte data samles i tabellen Observeret. Nulhypotesen om uafhængighed mellem rækker og søjler afvises på et 5 % signifikansniveau. Det er vist på to måder:

    p-CHI-anden er sandsynligheden for at en Chi-i-anden fordelt stokastisk variabel er større end 15,21, når Chi-i-anden fordelingen har 6 frihedsgrader som der er tale om her. Da denne sandsynlighed er mindre en 5% (0,05) forkastes hypotesen

    Den anden måde er at beregne den kritiske værdi for fordelingen på et 5 %-signifikansniveau. Den kritiske værdi er 12,59. Da teststørrelsen er større end den kritiske værdi, forkastes nulhypotesen.

  2. De forventede værdier beregnes ud fra de observerede. Man ganger række og søjlesummer og dividerer hvert produkt med den overordnede sum 1497.

    Teststørrelsen 15,21 er beregnet i tabel 3. Man bruger formlen (forventet - observeret)2/forventet.

  3. Afvigelserne mellem landsdelene ligger først og fremmest på profil A, de andre profiler ligger tæt på gennemsnittet, hvilket ses af at teststørelserne er tæt på 0.

    Med hensyn til profil A ligger jyderne på gennemsnittet, mens Københavnerne ligger over og sjællænderne under.

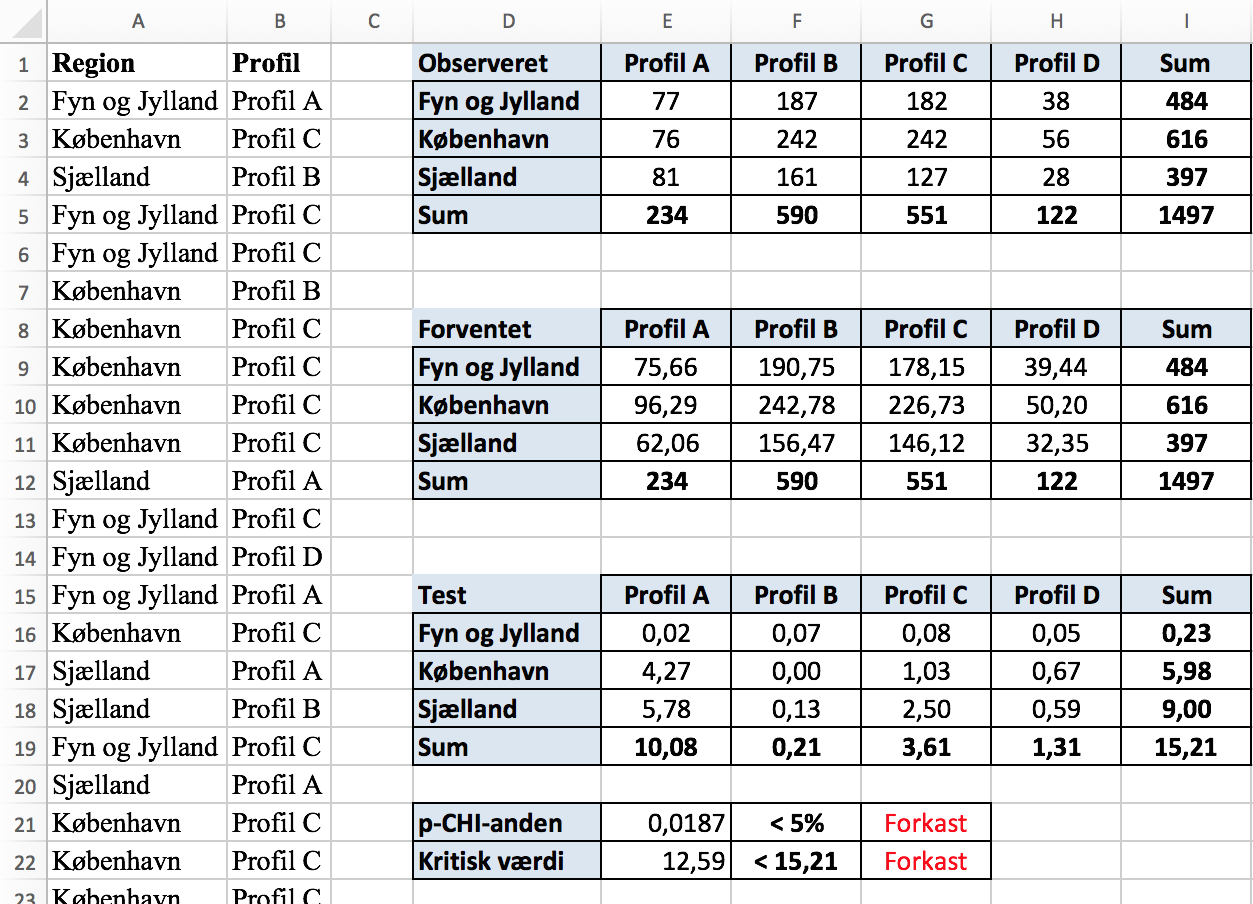
    4. (Se også Excel-filen Pension for at få formlerne.)

Svar på opgave 10:

  1. Nedenstående figur viser et diagram med tendenslinje for kursudviklingen i Excel.

    Af figuren følger, at a = 7,99 og b = 637

  2. Nedenstående figur viser en regressions-dataanalyse over kursudviklingen i Excel.

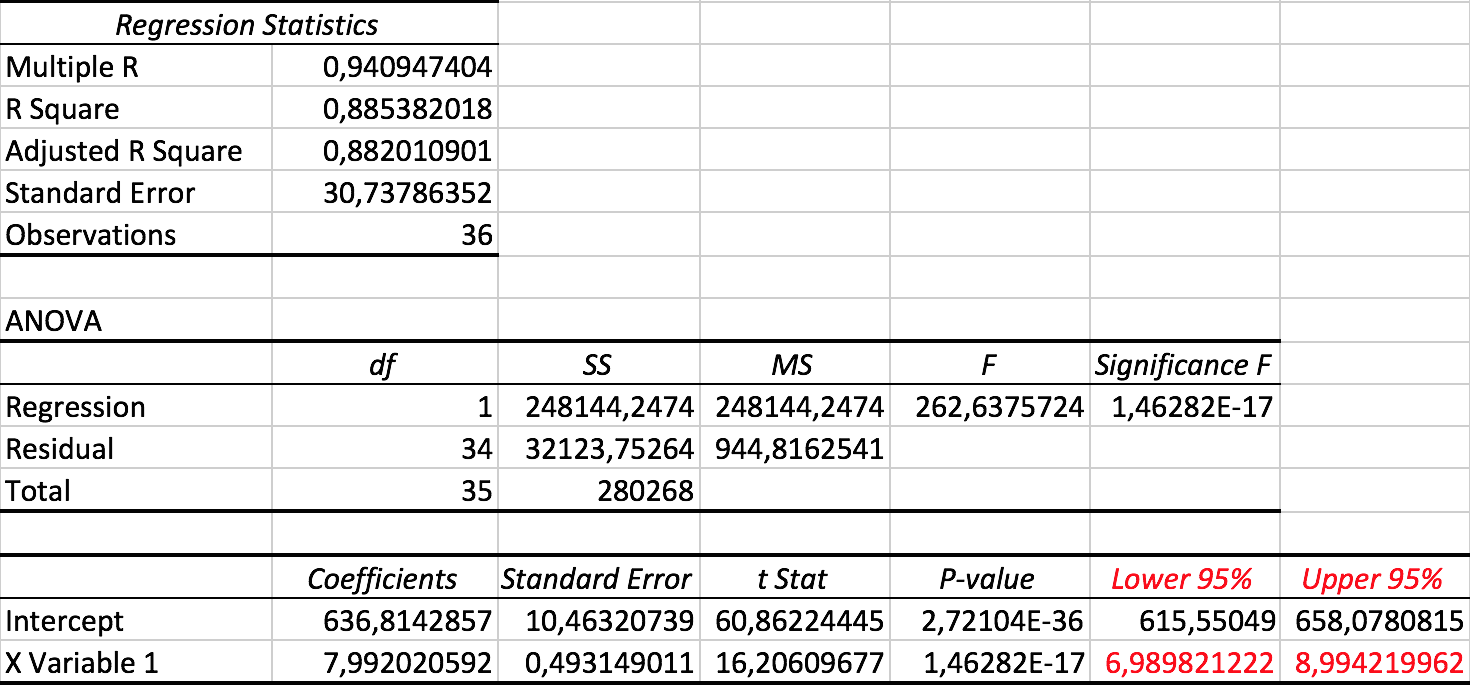
    Af tallene fremgår at 95 %-konfidensintervallet for a er [6,99;8,99]

  3. a viser, at kursen stiger med 8 procentpoint om ugen i gennemsnit. Kurser skifter hurtigt, så man skal nok være forsigtig med at investere for meget i aktien.

    4. (Se også Excelfilen Aktiekurs).

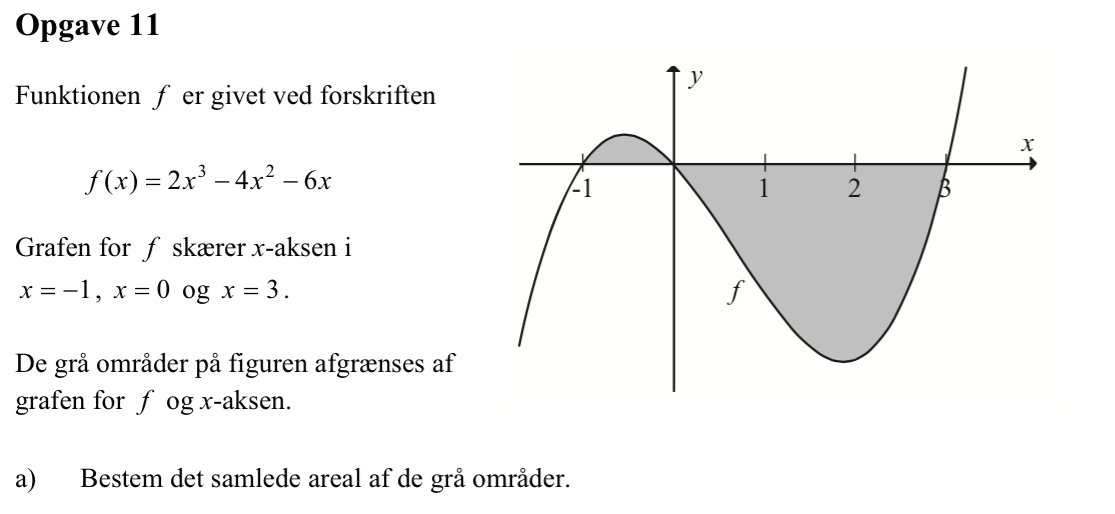
Svar på opgave 11:

  1. Arealet er lig med integralet af f(x) numerisk fra x = -1 til x = 3. Man får i Ti-Nspire:

    f(x):= 2*x3 - 4*x2 - 6*x ▸ Udført

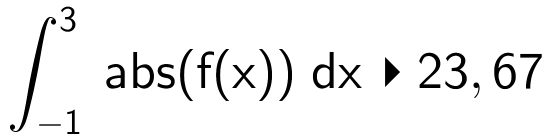
    Dvs. arealet af de grå områder er 23,67

Svar på opgave 12a:

  1. Nedenstående beregning i Excel viser indestående for hvert år:

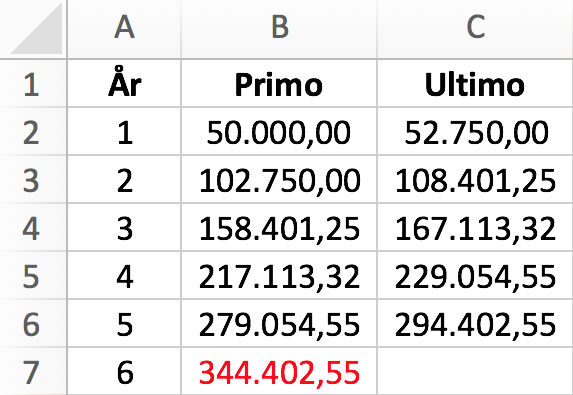
    Indestående 6. år umiddelbart efter indbetaling (og før rentetilskrivning) er 344.402,55 kr.

  2. Nedenstående beregning i Excel viser udviklingen over de 10 år, hvor renten ændres efter femte år:

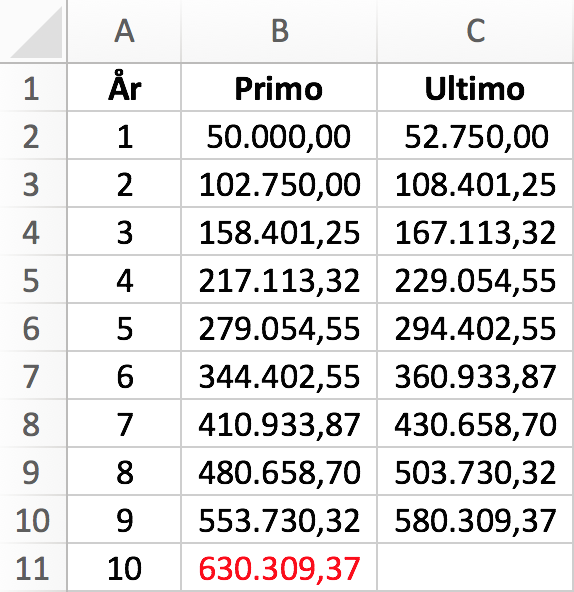
    Indestående 10. år umiddelbart efter indbetaling (og før rentetilskrivning) er 630.309,37 kr.

    3. (Se også Excel-filen Opsparing angående formler.)

Svar på opgave 12b:

  1. Man bruger Ti-Nspire kommandoen:

    deSolve(y'=5-0.1*y and y(0)=500,x,y) ▸ y=450.*(0.904837)x+50.

    Dvs. løsningen er p(t) = 450·(0.9048)t + 50 kr.

  2. Man bruger Ti-Nspire kommandoen:

    solve(450.*(0.904837)x+50.=75,x) ▸ x=28.90

    Dvs. tidspunktet, hvor værdien er nået ned på 75 kr., er: 28,9 uger

Svar på opgave 12c:

  1. N(240.000) er en niveaukurve med ligningen: -x2 + 800x - 0,25y + 300y = 240.000. For en kurve med en ligning på formen: ax2 + bx + cy2 + dy + e = 0 gælder, at har a og c samme fortegn er kurven en ellipse.

    I dette tilfælde er a = -1 og c = -0,25, dvs. a og c er begge negative, og N(240.000) er dermed en ellipse.

  2. Optimumspunktet i følge Hallings formler er O = -a·x02 - c·y02 + e, hvor x0 = -b/(2a) = og y0 = -d/(2c). Her er a = -1, b = 800, c = -0,25, d = 300 og e = 0.

    Dvs. man får: x0 = -800/(-2) = 400, y0 = -300/(2·(-0,25)) = 600.

    O = -(-1)·(400)2 = -800 - (-0,25)·(600)2 = 160.000 + 90.000 = 250.000. Da a < 0 er dette et maksimum.

    Da optimumspunktet (x,y) = (400,600) ligger inden for polygonområdet er O = 250.000 lig med maksimum for f.

Opgave b) løst med Excel Problemløser (løsning fremhævet med rødt):

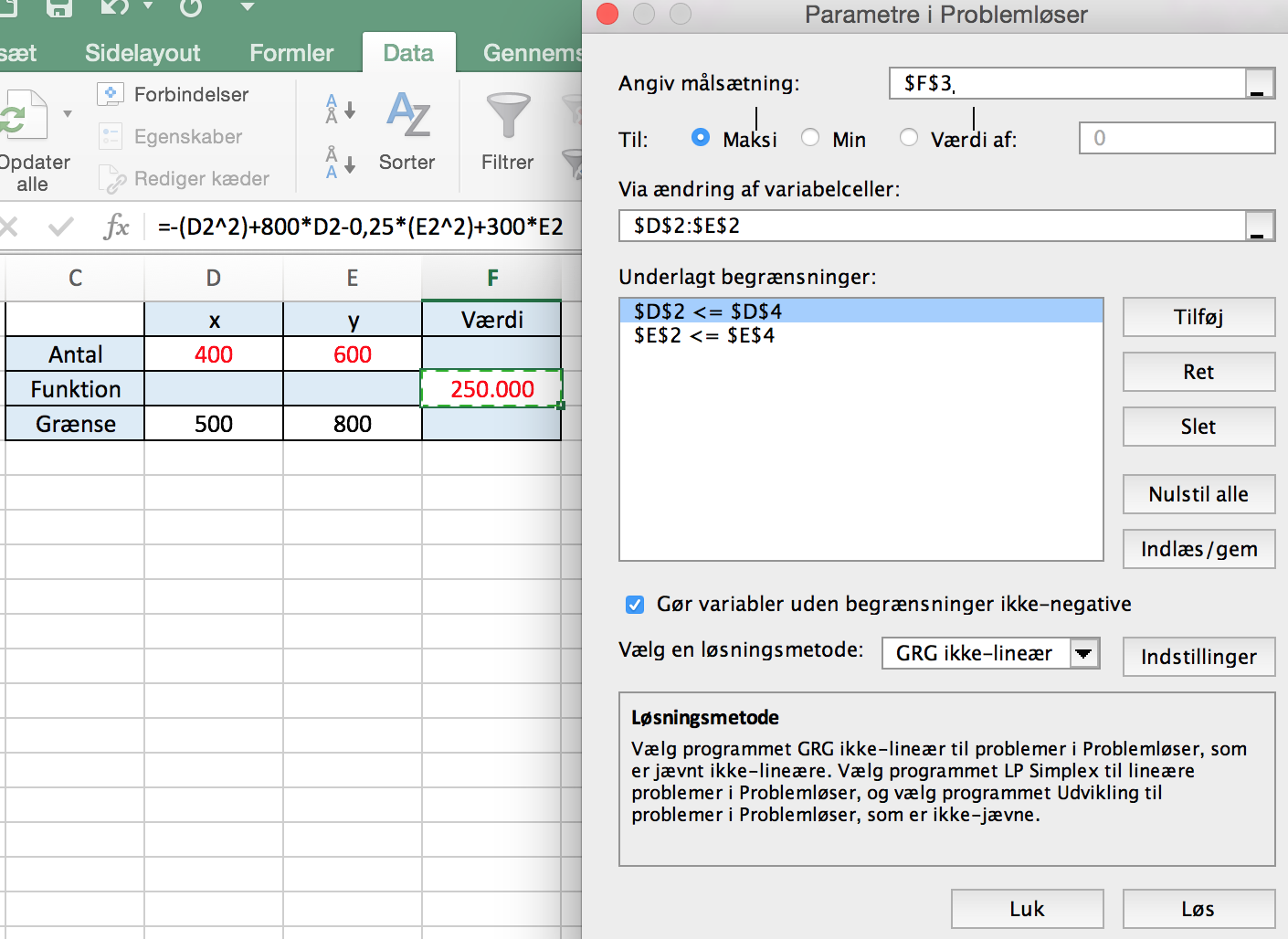
Problemløser installeres med: Funktioner > Excel-tilføjelsesprogrammer > Solver Add In.

(Se ogsp Excel-filen Optimering)