Svar på opgave 1:

1. Man bruger formlen for cosinus til vinklen mellem vektorerne:

   cos(v) =

   (2·(-4)+(-1)·2)/(√[2²+(-1)²]·√[(-4)²+(2)²]) =

   (-8-2)/(√[4+1]·√[16+4]) =

   -10/(√[5]·√[20]) =

   -10/√[100] =

   -1

   Dvs. cos(v) = -1, hvilket betyder, at vinklen mellem dem er 180°, og dermed er a og b parallelle.

Svar på opgave 2:

1. Man finder det ubestemte integrale ved hjælp af reglen om integration af potensfunktioner og reglen om integration af en sum:

   _∫(5x⁴ - 9x² + 4x - 1) dx = x⁵ - 3x³ + 2x² - x

Svar på opgave 3:

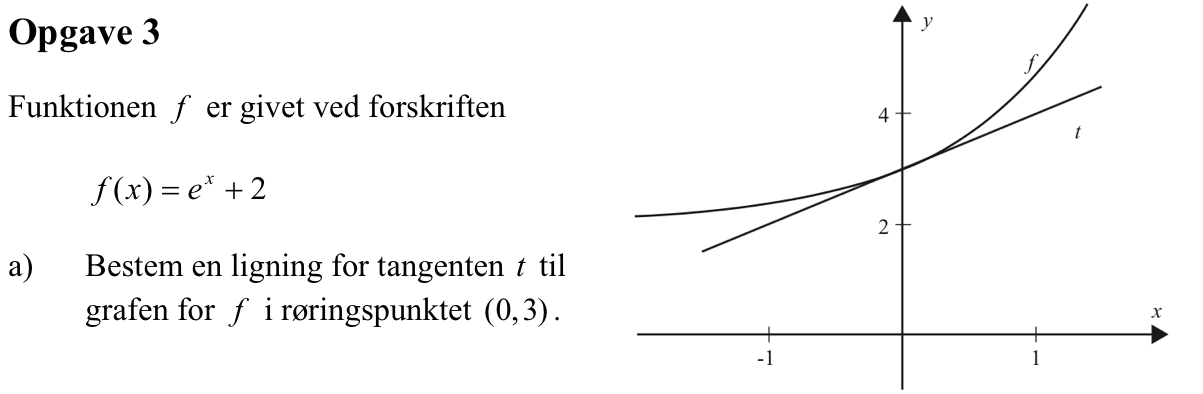
1. f(x) = e^x + 2. Tangentens ligning er

   y = f´(x₀)·(x-x₀) + f(x₀), hvor x₀ = 0.

   f´(x) = e^x dvs. f´(0) = e⁰ = 1. Dette giver:

   y = 1·(x - 0) + (e⁰ + 2) ⇒

   y = x + 3

Svar på opgave 4:

1. Forskriften er f(x) = 2000·1,1^x, hvor f(x) er antallet af robotter, og x er antal år efter 2001.

Svar på opgave 5:

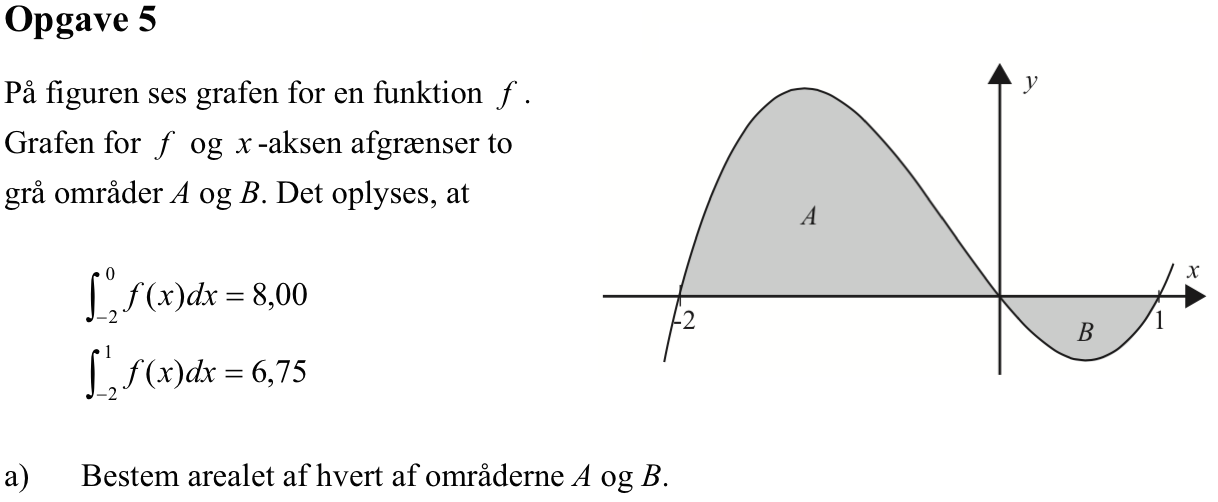
1. Man har, at integralet af f(x) fra x = -2 til x = 0 er lig med arealet af A.

   Integralet af f(x) fra x = -2 til x = 3 er lig med arealet af A minus arealet af B.

   Man får derfor, at arealet af A = 8,00 og

   arealet af B = 8,00 - 6,75 = 1,25

Svar på opgave 1:

1. Man opretter en liste med antallet af minutter i Ti-Nspire:

   minutter:={15,30,45,60,75,90,105} ▸ {15,30,45,60,75,90,105}

   Man opretter derefter en liste med antal jobs:

   antal_jobs:={0,21,21,28,12,8,5} ▸ {0,21,21,28,12,8,5}

   Ud fra den sidste liste laver man en liste over de summerede frekvenser:

   frekvens_sum:=(cumulativeSum(antal_jobs)/(sum(antal_jobs))*1. ▸ {0.,0.221053,0.442105,0.736842,0.863158,0.947368,1.}

   

2. Typeintervallet er det interval af minuttal, som har den største hyppighed. Dette interval er 45 - 60 minutter.

   Man beregner gennemsnittet eller middeltallet med følgende formel, hvori man benytter tallene fra de to første lister:

   (((30+15)/2)*21+((45+30)/2)*21+((60+45)/2)*28+((75+60)/2)*12+((90+75)/2)*8+((105+90)/2)*5)/95. ▸ 49.3421

   Dvs. gennemsnittet er 49,3 minutter, der er den tid de ansatte i gennemsnit bruger på en opgave.

   Middeltallet bruges til at finde variansen af minuttallene ved hjælp af formlen:

   ((((30+15)/2)-49.342)²*21+(((45+30)/2)-49.342)²*21+(((60+45)/2)-49.342)²*28+(((75+60)/2)-49.342)²*12+(((90+75)/2)-49.342)²*8+(((105+90)/2)-49.342)²*5)/94. ▸ 454.283

   Ud fra dette findes spredningen:

   √(449.501) ▸ 21.2014

   Spredning er 21,2 og viser hvor langt måleværdierne i gennemsnit ligger fra middeltallet. Variansen er dette tal i anden.

   Kvartilsættet findes ud fra sumkurven som de minuttal, der svarer til frekvenserne 25 %, 50 % og 75 %.

   

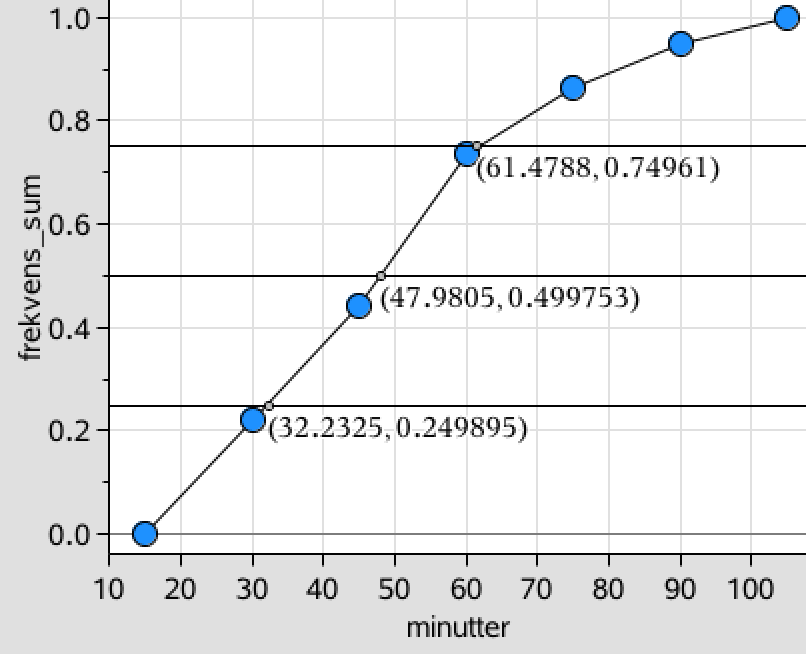
   Kvartilsættet er: nedre kvartil = 32 minutter, median = 48 minutter og øvre kvartil = 61 minutter

   Nedre kvartil er det antal minutter, som 25 % af de ansatte højst anvender på rengøringsopgaven. Tilvarende er medianen det antal minutter som halvdelen af de ansatte højst anvender på opgaven og øvre kvartil er det antal minutter som 75 % af de ansatte højst anvender på opgaven.

Svar på opgave 2:

1. Man opretter vektorerne i Ti-Nspire:

   a:=[t-1,1] ▸ [t-1,1]

   b:=[2,t] ▸ [2,t]

   Dernæst sætter man vektorerne ind i formlen for cosinus til vinklen mellem dem og løser den fremkomne ligning med hensyn til vinklen, idet t sættes lig med 1:

   solve(cos(x*1.°)=dotP(a,b)/(norm(a)*norm(b)),x)|t=1 and 0<x<180 ▸ x=63.4349 ("*1.°" sikrer at der regnes i grader)

   Dvs. vinklen mellem a og b er 63,4°, når t = 1

2. Vektorerne er parallelle, når cosinus til vinklen mellem dem er ±1, eller når den numeriske værdi af cosinus til vinklen er 1. Det giver følgende ligning i t:

   solve(abs(dotP(a,b))/(norm(a)*norm(b))=1,t) ▸ t=−1 or t=2

   Dvs vektorerne a og b er parallele, når t = -1 eller t = 2

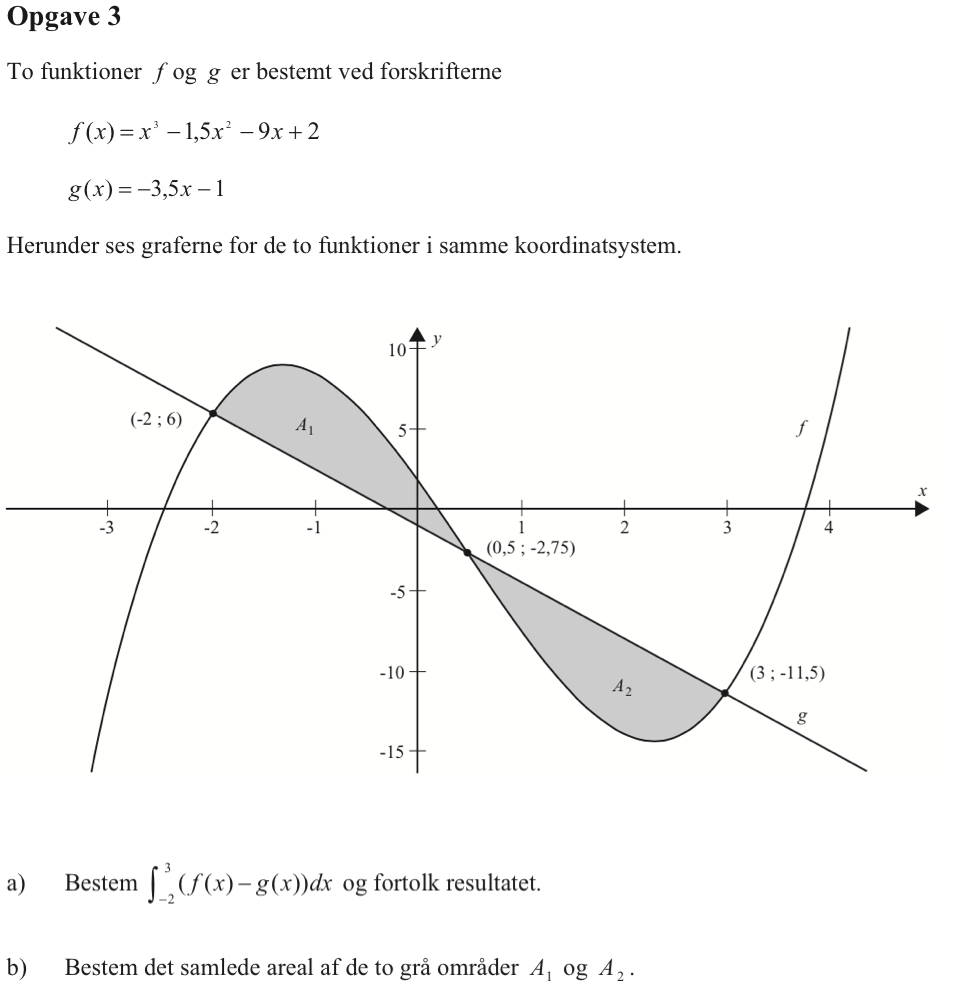
Svar på opgave 3:

1. Man opretter funktionerne f(x) og g(x) i Ti-Nspire:

   f(x):=x³-1.5*x²-9*x+2 ▸ Udført

   g(x):=−3.5*x-1 ▸ Udført

   Man finder integralet i Ti-Nspire:

   integral(f(x)-g(x),x,−2,3) ▸ 0.

   Dvs. integralet er 0 og dermed er de to arealer A₁ og A₂ er ens.

2. Arealet af de to områder er lig med integralet af |f(x) - g(x)| fra x = -2 til x = 3.

   integral(abs(f(x)-g(x)),x,−2,3) ▸ 19.5313

   Dvs. det samlede areal af de A₁ og A₂ er 19,5

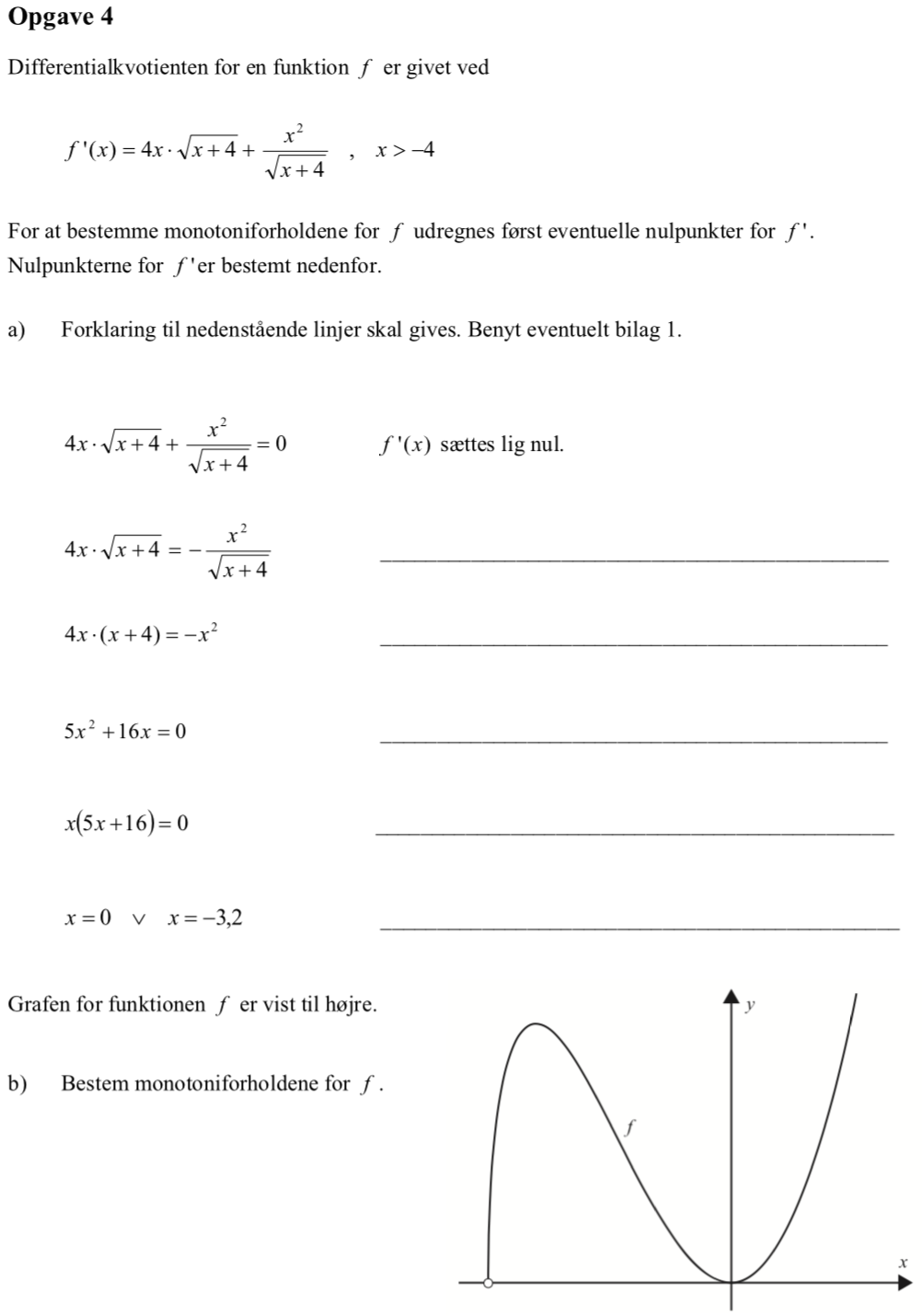
Svar på opgave 4:

1. Man får:

   

2. Man finder nulpunkterne for f´(x) (kaldet fm(x)) i Ti-Nspire:

   fm(x):=4*x*sqrt(x+4)+x²/sqrt(x+4) ▸ Udført

   solve(fm(x)=0.,x) ▸ x=−3.2 or x=0.

   Man får at f´(x) = 0 for x = -3,2 og x = 0. Man laver en fortegnsundersøgelse ved hjælp af værdier af x før mellem og efter nulpunkterne. For x = -3,5 får man i Ti-Nspire:

   fm(−3.5) ▸ 7.42462

   fm(−3) ▸ −3

   fm(1.) ▸ 9.39149

   Det ses at f´(-3,5) > 0, f´(-3,0) < 0 og f´(1,0) > 0. Dvs.

   f er voksende for -4 < x < -3,2, f er aftagende for -3,2 < x < 0 og f er voksende for x > 0

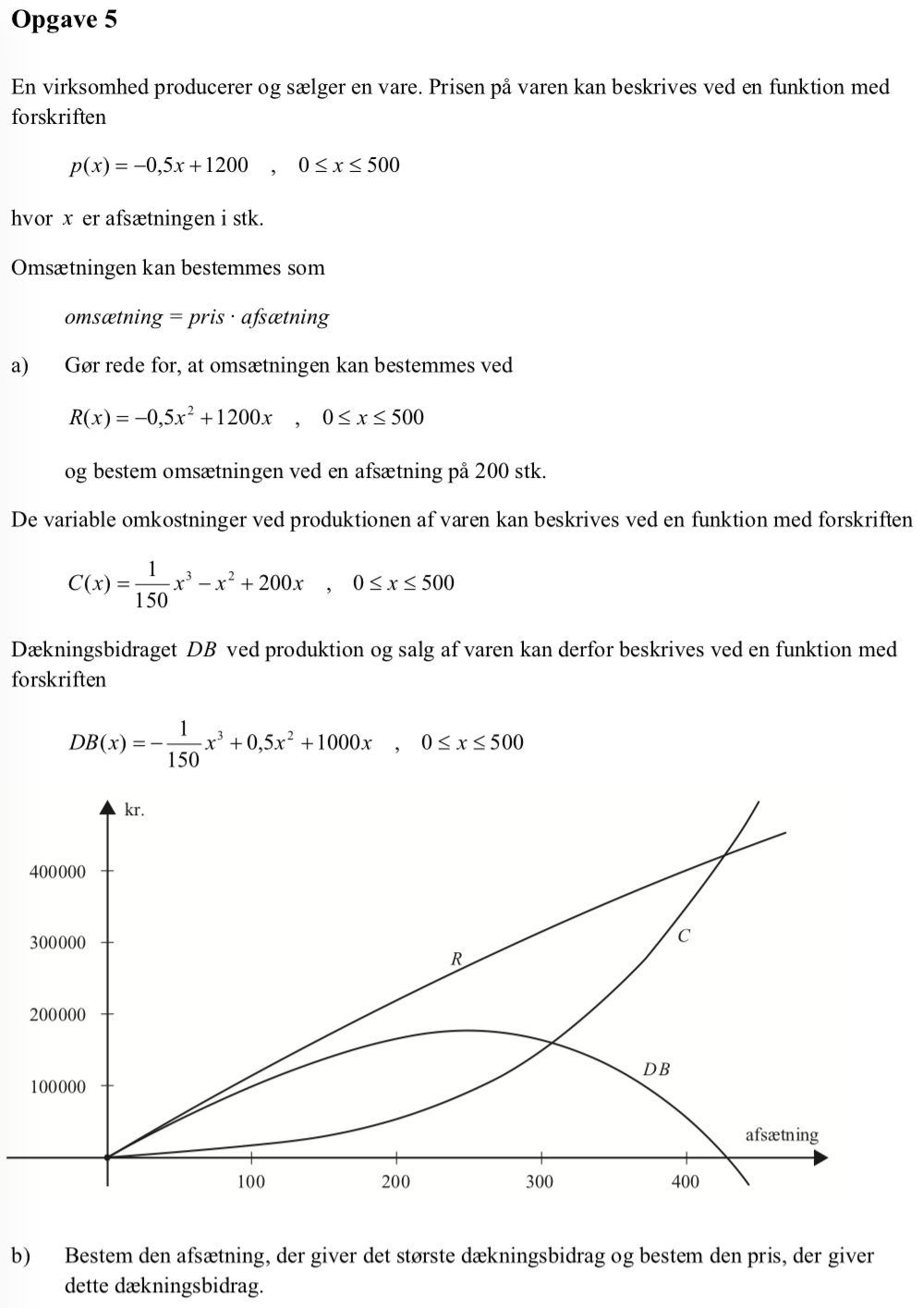
Svar på opgave 5:

1. Omsætning = afsætning·pris = x·p(x) = -0,5x² + 1200x

2. Man opretter dækningsbidraget db(x) i Ti-Nspire:

   db(x):=(−1/150)*x³+0.5*x²+1000*x ▸ Udført

   Man finder størsteværdien af dækningbidraget ved hjælp af fMax-kommadnoen:

   fMax(db(x),x)|0<x<500 ▸ x=250.

   Dvs. den afsætning, der giver det største dækningsbidrag er 250 stk.

   Prisen ved denne afsætning er -0,5x·250 + 1200 kr. = 1075 kr.

Svar på opgave 6:

1. Man opretter p(x), q(y) i Ti-Nspire:

   p(x):=−5*x+1200 ▸ Udført

   q(y):=−2*y+800 ▸ Udført

   Dette indsættes i udtrykket for db(x,y)

   db(x,y):=x*(p(x)-400)+y*(q(y)-200) ▸ Udført

   Forskriften for db(x,y) bliver:

   db(x,y) ▸ −5*x²+800*x-2*y²+600*y

   ...som ses at være det, man skulle vise.

2. Ligningen for N(70000) er: −5x² + 800x - 2y² + 600y = 70000

   Ligningen kan opskrives ved hjælp af kommandoen completesquare i Ti-Nspire:

   completeSquare(−5*x²+800*x-2*y²+600*y=70000,x,y) ▸ −5*(x-80)²-2*(y-150)²=−7000

   Dvs. ligningen kan omskrives til

   5·(x-80)² + 2·(y-150)² = 7000 ⇒

   ((x-80)/37,417)² + ((y-150)/59,161)² = 1

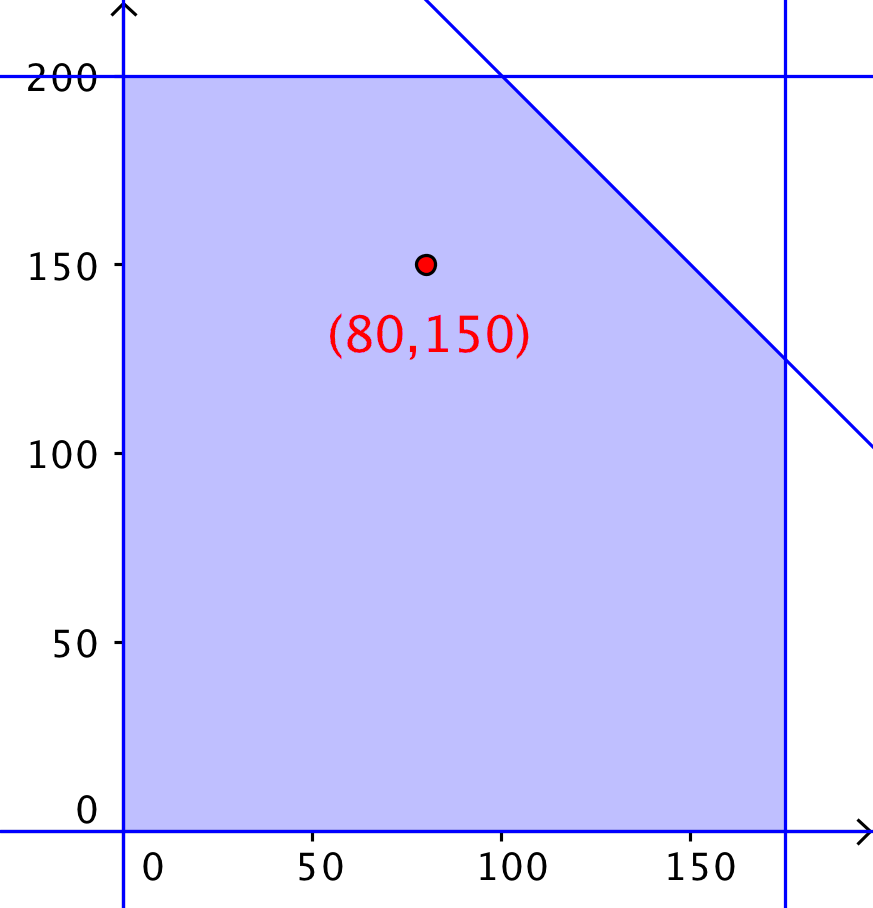
   Dette ses at være ligningen for en ellipse med lilleakse = 37,417 i x-aksens retning og storakse = 59,161 i y-aksens retning. Skæringspunktet for lilleaksen og storaksen er (x,y) = (80,150).

   Niveaukurven N(70000) er vist på tegningen nedenunder, som er lavet i Geogebra.

   

3. Funktionen for dækningsbidraget har maksimum i skæringspunktet mellem lilleaksen og storaksen for de ellipser, der udgør niveaukurverne for dækningsbidraget.

   Dette skæringspunkt er som nævnt: (x,y) = (80,150). Dvs. det største dækningsbidrag forekommer ved et salg af

   80 enheder af A og 150 enheder af B

   Optimumspunktet er vist på tegningen nedenunder, som er lavet i Geogebra. Det blå område er det begrænsende polygon.

   

Svar på opgave 7:

1. Graf 1 har nulpunkt for en x = -1, hvor graf 2 har et ekstremum. Dette ses nedenunder.

   

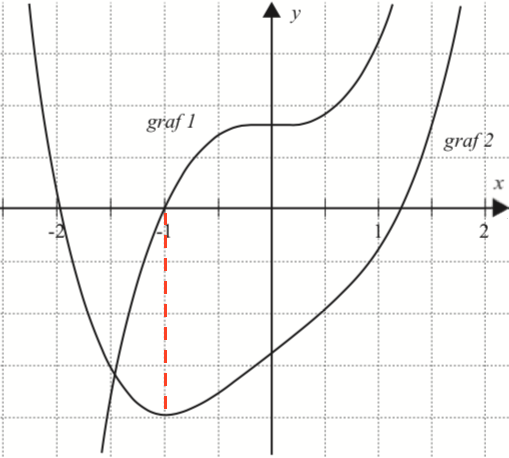
   Dermed er graf 2 grafen for f, og graf 1 er grafen for den afledede af f.

Svar på opgave 8:

1. Man opretter f(x) i Ti-Nspire:

   f(x):=−x³+3*x²+24*x+k ▸ Udført

   For at finde monotoniintervallerne skal man finde f´(x) og løse ulighederne f´(x) < 0 og f´(x) > 0. Det gøres i Ti-Nspire:

   solve(derivative(f(x),x)<0,x) ▸ x<−2 or x>4

   solve(derivative(f(x),x)>0,x) ▸ −2<x<4

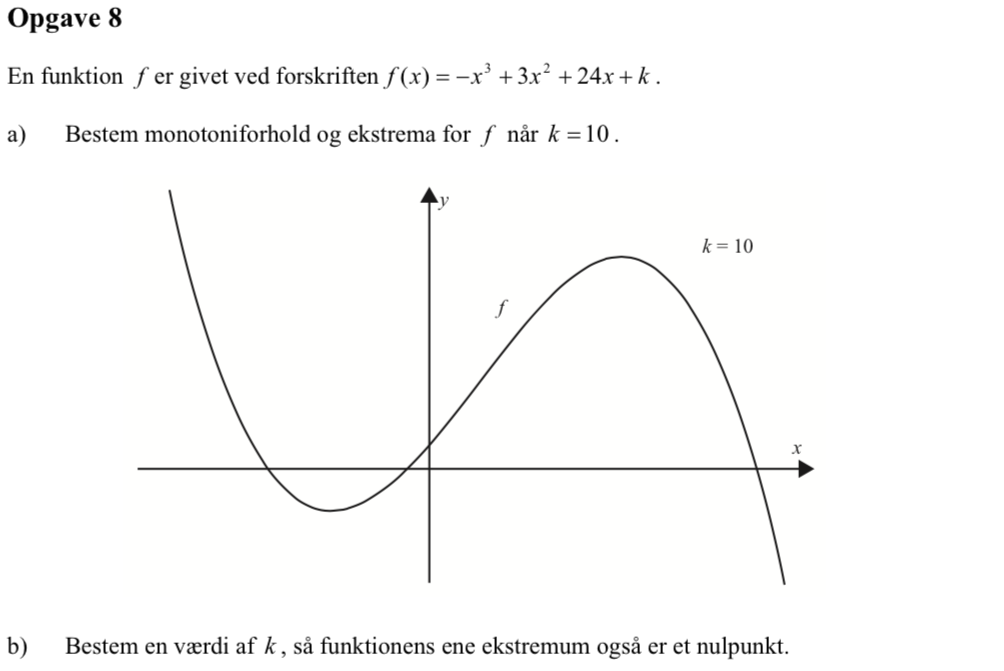
   Det ses heraf, at f aftager for x < -2, vokser for -2 < x < 4 og aftager for x > 4

   For at finde ekstremumspunkterne skal man løse ligningen f´(x) = 0. Dette gøres i Ti-Nspire:

   solve(derivative(f(x),x)=0,x) ▸ x=−2 or x=4

   x = -2 er lokalt minimum, da f aftager før x = -2 og vokser efter. Værdien af f bergnes i Ti-Nspire:

   f(−2)|k=10 ▸ −18

   Dvs den lokale minimumsværdi for f, når k = 10, er -18

   x = 4 er et lokalt maksimum, da f vokser før x = 4 og aftager efter.

   f(4)|k=10 ▸ 90

   Dvs den lokale maksimumsværdi for f, når k = 10, er 90

2. Man skal finde de sammenhørende værdier af x og k, hvoraf det gælder, at f(x) = 0 og f´(x) = 0. Man får følgende i Ti-Nspire:

   solve(f(x)=0 and derivative(f(x),x)=0,x,k) ▸ x=−2 and k=28 or x=4 and k=−80

   Dvs. for k = 28 er den lokale minimumsværdi for f i x = -2 også et nulpunkt.

   For k = -80 er det lokale maksimum for f i x = 4 også et nulpunkt for f.

Svar på opgave 9a:

1. Man bruger formlen for ydelse for annuitetslån i Ti-Nspire:

   6000*(0.0383/(1-1.0383^-12) ▸ 633.023

   Dvs. den ydelse, som hun skal betale er 633,0 kr.

2. Den effektive årlige rente beregnes med formlen:

   1.0383¹²-1 ▸ 0.569908

   Dvs den effektive årlige rente er 0,5699 = 57 %

Svar på opgave 9b:

1. f(x,y) = 28000x + 36000y. Man opretter niveaukurven f(x,y) = 0, som har ligningen 28000x + 36000y = 0 ⇒ y = 0,78x.

   Denne linje parallelforskydes til den rammer polygonet som vist på figuren nedenunder.

   

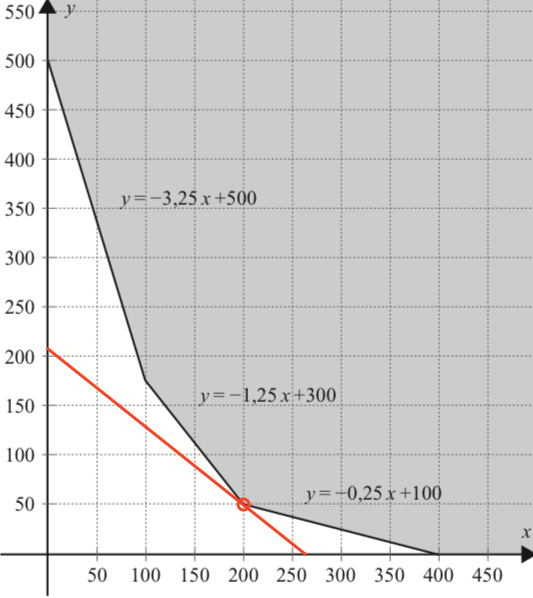
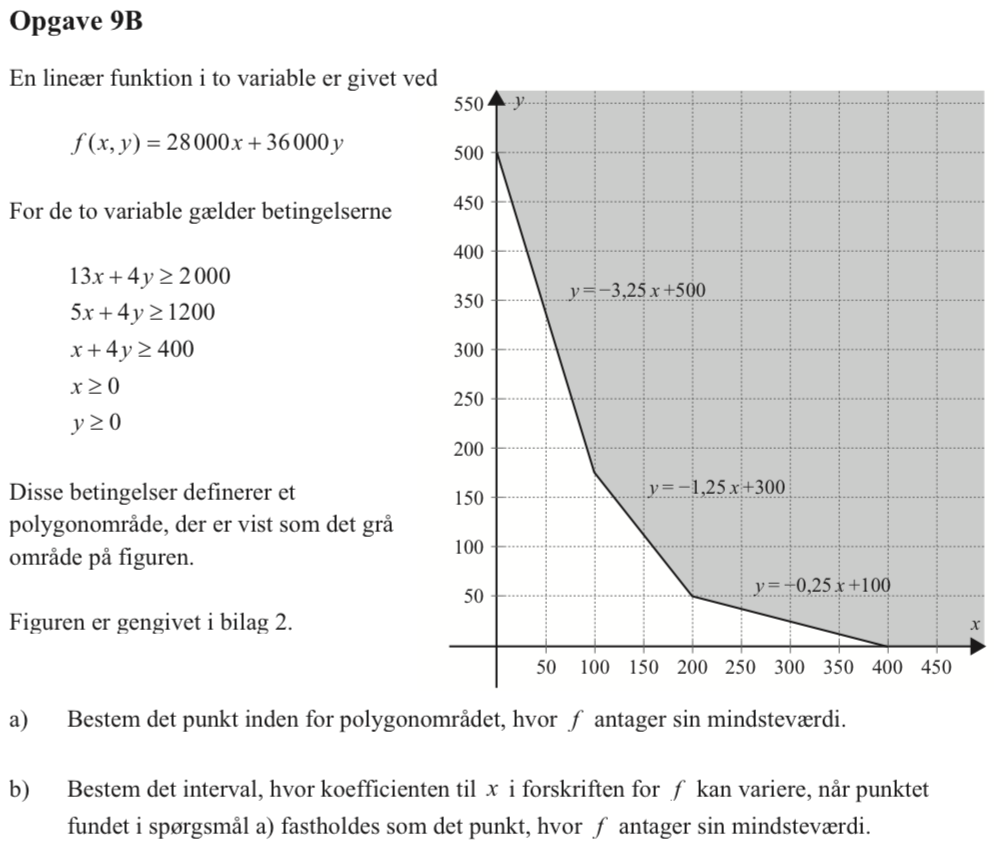
   Dette røringspunkt er (x,y) = (50,200). Dvs. f antager sin minimumsværdi for x = 50 og y = 200

2. Man skal finde hældningen af de linjer, der støder op til minimumspunktet.

   Den ene linje er y = -0,25x + 100 og den anden er y = -1,25 + 300.

   Man sætter koefficienten til x lig med a i udtrykket for f: f(x,y) = ax + 36000y ⇒ y = -(a/36000)x + f(x,y)/36000

   Man skal finde a, så -a/36000 = -0,25 eller -a/36000 = -1,25. Det giver: a = 36000·0,25 = 9000 eller a = 1,25·36000 = 45000.

   Dvs. koefficienten til x skal ligge mellem 9000 og 45000