Svar på opgave 1:

1. Kapitalformlen giver: K = 15.000·(1,0265)⁴ = 16.654,33

   Dvs. efter 4 år står der: 16.654,33 kr. på kontoen.

2. Det indsatte beløb kaldes x. K = x·(1,03)⁴ = 12.830,80 ⇒ x = 12.830,80/(1,03)⁴ = 11.400,00

   Dvs. det indsatte beløb var: 11.400,00 kr.

Svar på opgave 2:

1. Der er tale om positiv lineær vækst, da antallet af biler vokser med et bestemt tal om året. f(x) er antallet af biler x år efter 2013.

   Formlen bliver f(x) = 0,035 (mio./år)·x + 2,237 mio

2. Man skal finde det x hvorom det gælder, at 0,035 (mio./år)·x + 2,237 mio = 2,4 mio. Man får:

   0,035·x + 2,237 = 2,4 ⇒ 0,035·x = 2,400-2,237 ⇒ x = 0.163/0,035 = 4,7 år. Dvs. 2,4 mio. biler vil blive passeret i 2013 + 4 = 2017

Svar på opgave 3:

1. Antal sekunder = 17,4·75^0,25 = 51.2

2. Dobbelt så meget er det samme som 100% mere. Den procentvis forskel er: ((1 + 100%)^0,25 - 1)·100% = (2^0,25 - 1)·100% = 18,9%

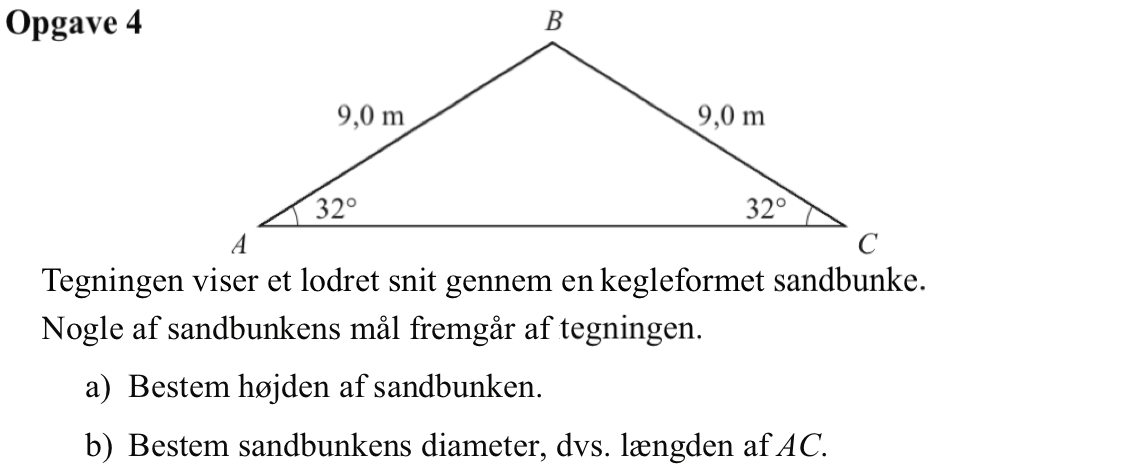
Svar på opgave 4:

Trekant ABC er ligebenet. Man kender benenes længde og grundvinklerne.

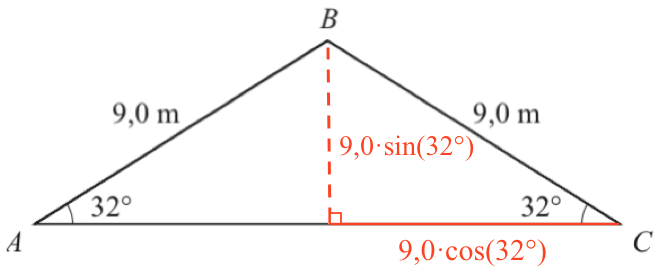
Højden i toppunktet B deler trekant ABC i to retvinklede trekanter som vist nedenunder. Den ene retvinkled trekanter kan bruges til at finde højde og grundlinje ved hjælp af de viste trigonometriske formler.

1. Højden er 9 m·sin(32°) = 4.77 m

2. Grundlinjens længde er 2·9 m·cos(32°) = 15.3 m

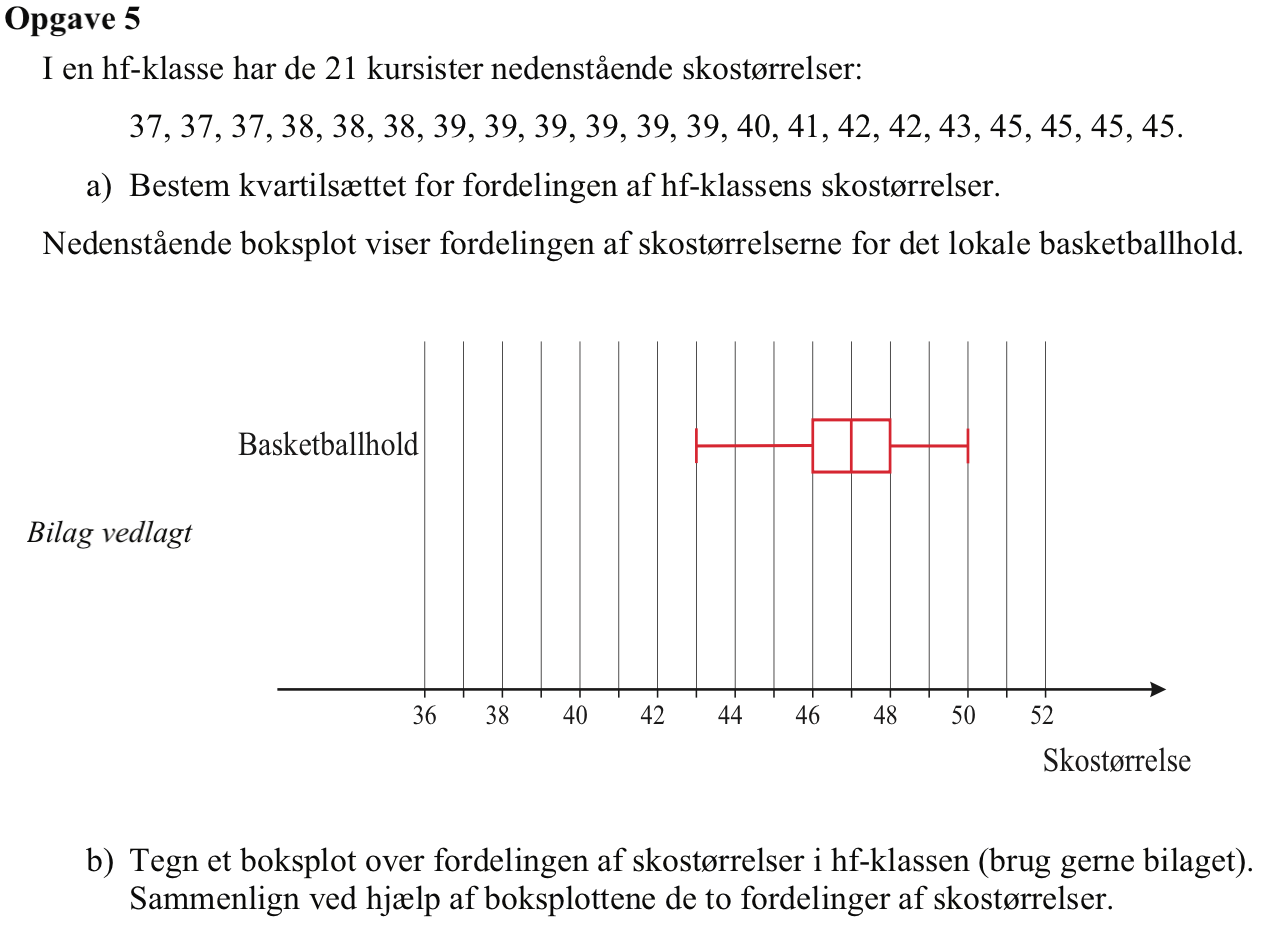
Svar på opgave 5:

1. Tallene er stillet op i rækkefølge. Det midterste tal er 39, som er medianen. Blandt de 10 mindste tal er tal nummer 5 og 6 begge lig med 38 dvs. 25%-fraktilen er 38. Blandt de 10 højeste tal er tal nummer 5 lig med 42 og tal nummer 6 lig med 43. Dvs. 75%-fraktilen er 42,5.

   Fraktilerne er: 25%: 38, 50%: 39 og 75%: 42.

2. Boksplot i Geogebra med deskriptorer tio venstre.

   

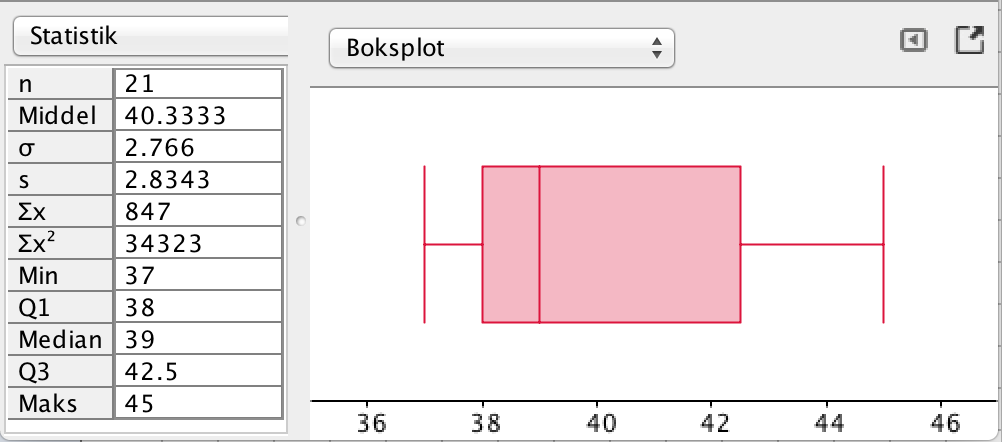
   Basketballspillernes sko er større. Alle fraktiler ligger højere end HF klassens.

Svar på opgave 6:

1. Man skal løse de sammenhørenden ligninger: 255 = b·a⁰ og 369 = b·a⁴ med hensyn til a og b, hvor a og b er positive tal. Man får:

   255 = b·a⁰ ∧ 369 = b·a⁴ ⇒

   255 = b ∧ 369 = b·a⁴ ⇒

   255 = b ∧ 369 = 255·a⁴ ⇒

   255 = b ∧ 369/255 = a⁴ ⇒

   b = 255 ∧ a = (369/255)^1/4 ⇒

   a = 1,0968 ∧ 255 = b

2. a er den faktor, som der ganges med for hver meter, man stiger i højden, og b er startbanens længde ved havoverfladen.

3. Fordoblingskonstanten er ln(2)/ln(a) = 0.693/ln(1,0968) = 0.693/0.0924 = 7,5 = 7.500 fod

   Dvs. startbanens længde fordobles for hver 7500 fod man stiger i højden.

Svar på opgave 7:

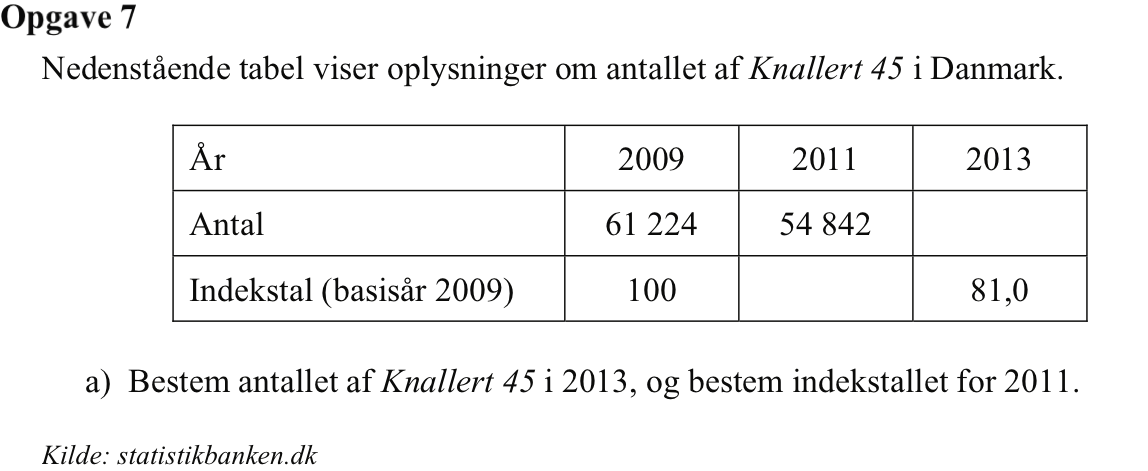
Skemaet udfyldes som vist: Antallet af knallerter i 2013 sættes til x og indekstallet for 2011 kaldes y.

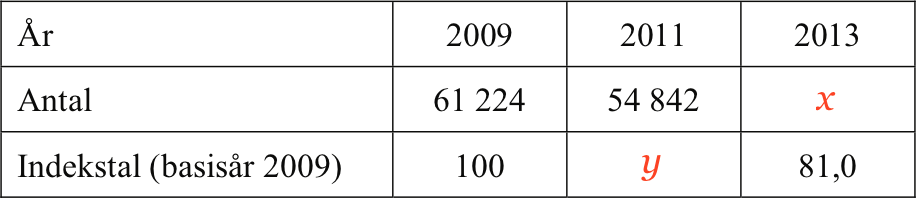
For hver år skal de tal, som står under årstallet med en brøkstreg imellem, give det samme, dvs.: 61.224/100 = 54.842/y = x/81.

1. Man finder antallet af knallerter i 2013 som x i ligningen: 61.224/100 = x/81 ⇒ x = 81·61.224/100 = 49.591,44

   Dvs. antallet af knallerter i 2013 er 49.591

   Indekstallet i 2011 findes som y i ligningen: 54.842/y = 61.224/100 ⇒ y = 54.842·100/61.224 = 89,6

   Dvs. indekstallet i 2011 er 90

Svar på opgave 8:

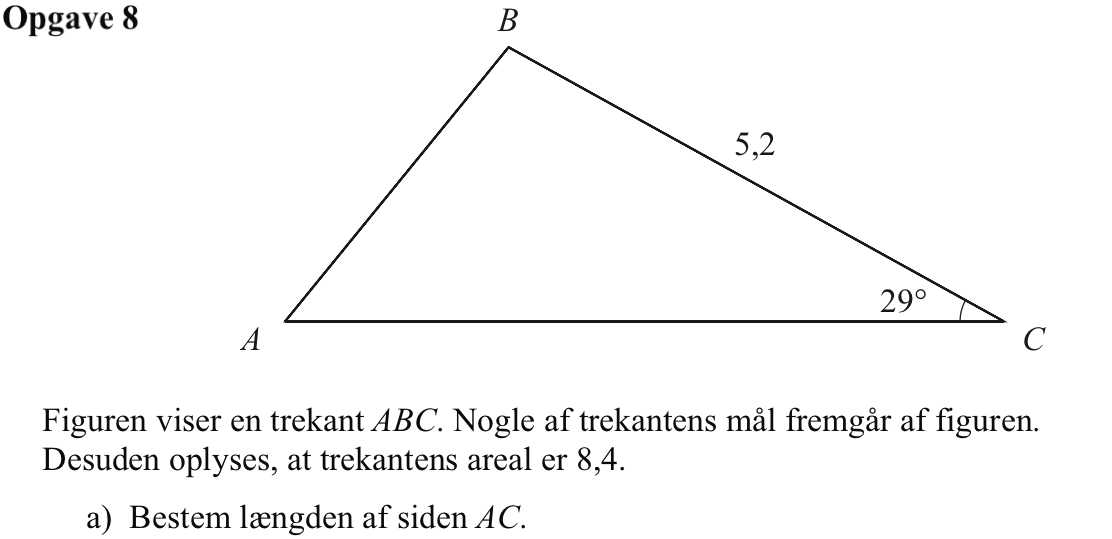
1. Man har at areal = ½·|AC|·højde ⇒ 8,4 = ½·|AC|·højde ⇒ |AC| = 2·8,4/højde.

   Højde = 5,2·sin(29°) = 2.521. Dette er vist nedenunder:

   

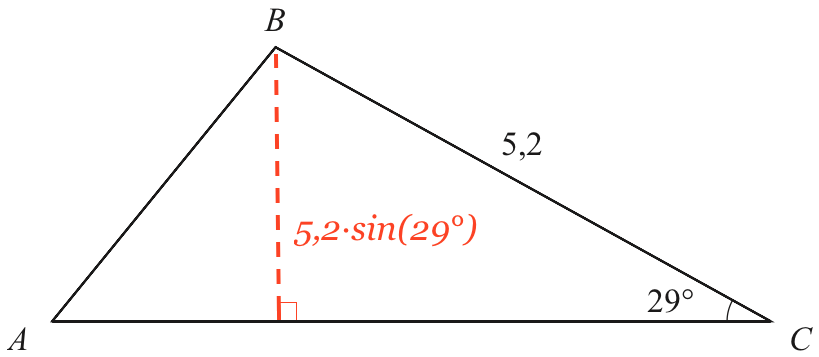
   Det giver: |AC| = 2·8,4/2.521 = 6,66