Svar på opgave 1:

1. Man finder beløbet, som står efter 5 år, ved hjælp af formlen for kapitalfremskrivning: K = K₀·(1 + r)ⁿ, hvor K₀ er startkapitalen, r er rentesatsen og n er antal terminer. Man får:

   K = 4000·(1 + 2,9%)⁵ kr. = 4000·(1,029)⁵ kr. = 4614,63 kr.

2. Man skal løse ligningen 4705 = 4000·(1 + r)⁵ med hensyn til r. Man får i Ti-Nspire:

   solve(4705.=4000*(1+r)⁵,r) ▸ r=0.032999

   Dvs. rentesatsen er = 0.033 = 3,3 %

Svar på opgave 2:

1. Der er tale om en negativ lineær udvikling (eller vækst).

   Modellen er f(x) = -439x + 28262,

   hvor f(x) er antallet af A-kassemedlemmer, x er antal år efter 2000 og minustegnet foran 439 kommer af, at antallet falder.

2. Man skal finde f(14) = -439·14 + 28262 = 22116

Svar på opgave 3:

1. Nedenstående tabel over boligstørrelse, frekvens og kummulerede frekvenser er lavet i Excel. Den øverste række af nuller er tilføjet for at få kurven til at møde x-aksen.

   

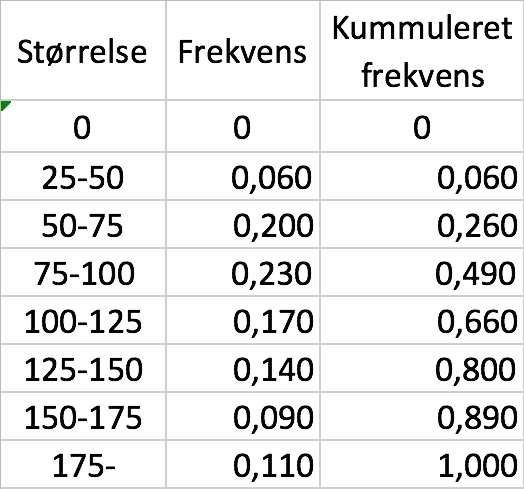
   Nedenstående sumkurve er tegnet ud fra tabellerne.

   

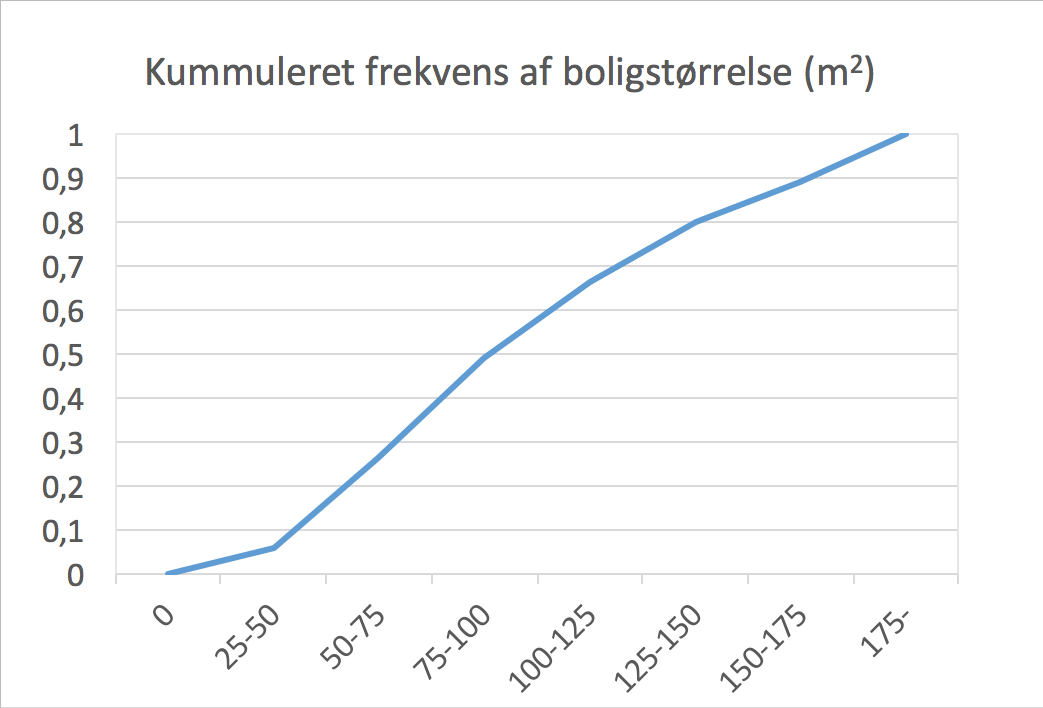
2. Man skal finde nedre grænse for de 25% af boligerne, der er størst. Dette gøres ved gå ud fra 75 % på sumkurven som vist nedenunder.

   

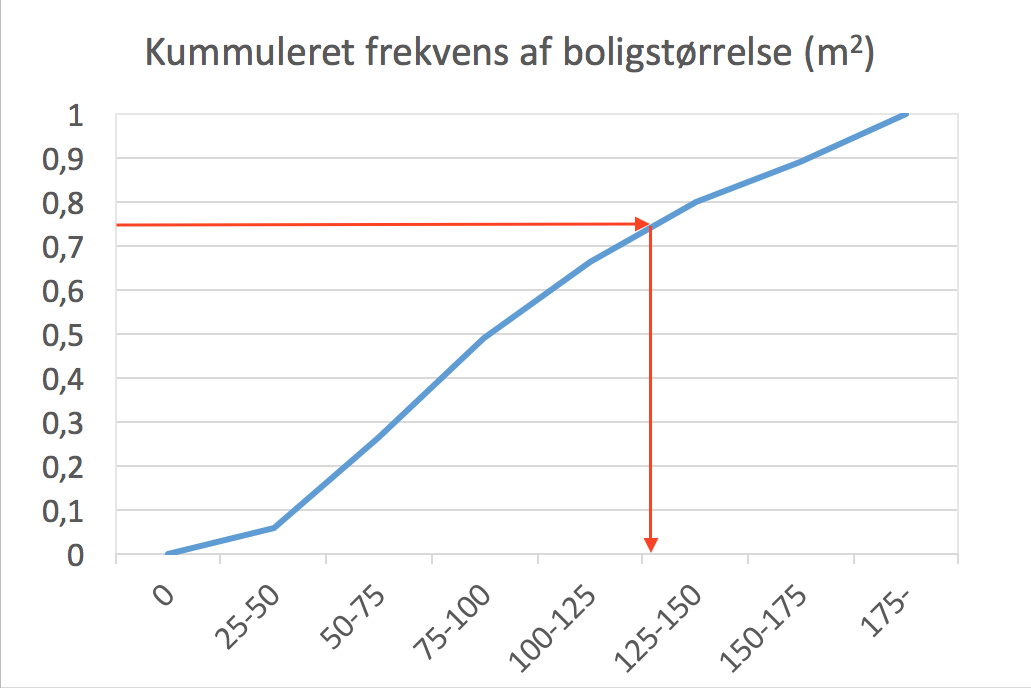
   Grænsen ses at ligge i starten af intervallet 125-150 ud for 127, dvs. de 25 % største boliger er over 127 m²

Svar på opgave 4:

1. Overfladearealet er 6·(1,8 cm)² = 19,44 cm²

   Man skal løse ligningen 6·x² = 13,5 med hensyn til x. Det giver:

   6·x² = 13,5 ⇔ x² = 13,5/6 ⇔ x = ±√(2,25) = ±1,5. Her tager man den positive løsning.

   Dvs. sidelængden af terningen er 1,5 cm

2. Formlen for overfladerealet er en potensfunktion. Man bruger formlen for procent-procent vækst, der gælder for potensfunktioner:

   (1,16² - 1)·100 % = 34,6 %

Svar på opgave 5:

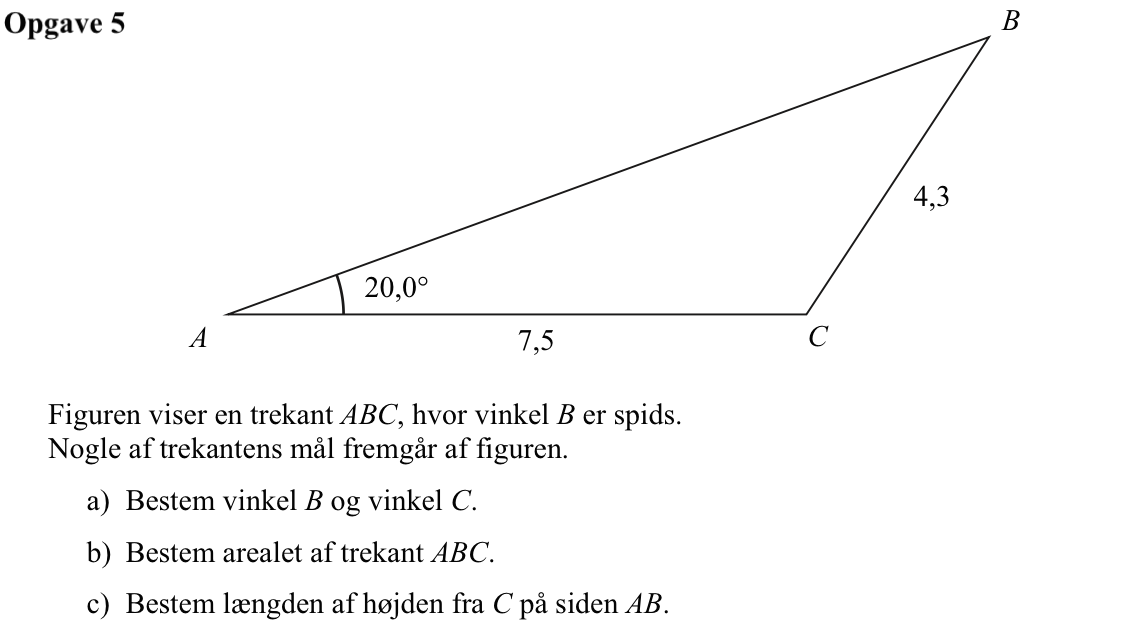
1. Man finder vinkel B ved hjælp af sinusrelationerne. Man får:

   sin(∠A)/a = sin(∠B)/b ⇒ sin(20,0°)/4,3 = sin(∠B)/7,5 ⇒ sin(∠B) = 7,5·sin(20,0°)/4,3 ⇒ ∠B = sin^-1(0,5965) ⇒ ∠B = 36,6°

   Vinkel C findes ved hjælp reglen om, at vinkelsummen i en trekant er 180°: ∠C = 180° - (20,0° + 36,6°) = 123,4°

2. Arealet er 0,5·|AC|·h_B = 0,5·|AC|·[|CB|·sin(∠C)] = 0,5·7,5·4,3·sin(123,4°) = 13,46

3. Højden h_C = |BC|·sin(∠B) = 4,3·sin(36,6°) = 2,56

Svar på opgave 6:

1. Man løser to ligninger med to ubekendte, en for hver lodret kollonne i tabellen, idet det øverste tal er x og det nederste er y:

   120 = b·a⁰ ∧ 108 = b·a⁴ ⇔

   120 = b·1 ∧ 108 = b·a⁴ ⇔

   b = 120 ∧ 108 = 120·a⁴ ⇔

   b = 120 ∧ a⁴ = 0,9 ⇔

   b = 120 ∧ a = ⁴√(0,9) ⇔

   a = 0,974 ∧ b = 120

2. Man skal løse ligningen 80 = 89·0,973^x ⇔

   0,973^x = 80/89 ⇔

   0,973^x = 0,89888 ⇔

   x·ln(0,973) = ln(0,89888) ⇔

   x = ln(0,89888)/ln(0,973) ⇔

   x = 3,8948

   Dvs. der går 3,9 uger før personens vægt er nede på 80 kg

3. Et ugentligt vægttab på 2,7 % svarer til at a i formlen y = b·a^x skal være 1 - 2,7 % = 1 - 0,027 = 0,973 hvilket stemmer med modellerne.

   Dermed er oplysningen fra producenten rigtig

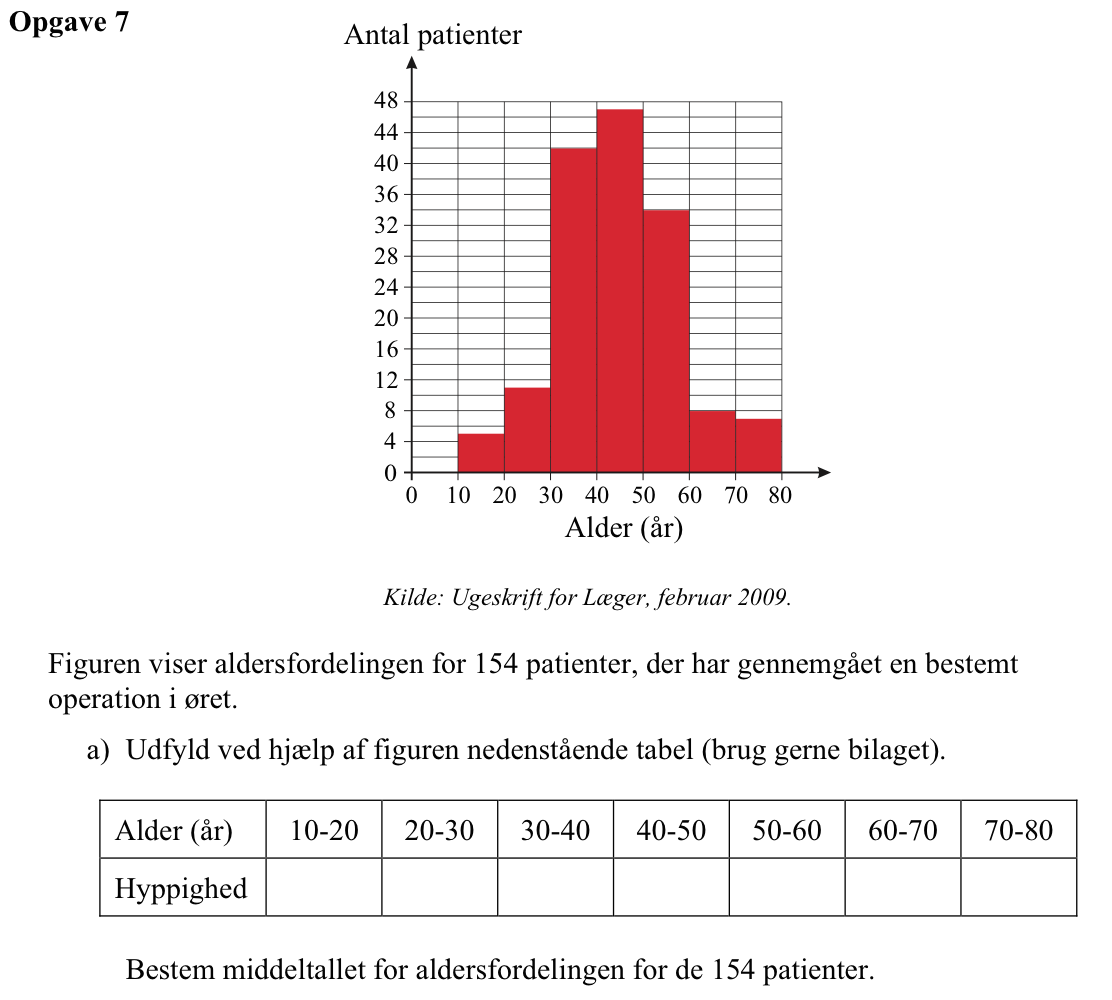
Svar på opgave 7:

1. Man aflæser hyppigheden som højden på hver af de røde søjler. Resultatet er vist som en liste på formen Alder: hyppighed,...

   10-20: 5, 20-30: 11, 30-40: 42, 40-50: 47, 50-60: 34, 60-70: 8, 70-80: 7

   Middeltallet for grupperede data fidnes ved tage summen af (hyppighed for interval)·(midten af interval) og dividere med antal patienter, dvs. middeltallet af patienternes alder er

   [5·(15 år) + 11·(25 år) + 42·(35 år) + 47·(45 år) + 34·(55 år) + 8·(65 år) + 7·(75år)]/154 = 44,5 år