Svar på opgave 1:

1. Man finder det oprindelige beløb K₀ ved hjælp af formlen for kapitalfremskrivning: K = K₀·(1 + r)ⁿ, hvor K₀ er startkapitalen, r er rentesatsen, og n er antal terminer. Man får: 10327,31 kr. = K₀·(1,012)⁷. Dette løses i Ti-Nspire, hvor K₀ kaldes x:

   solve(10327.31=x*1.012⁷,x) ▸ x=9500.

   Dvs. der blev indsat 9500 kr. på kontoen.

Svar på opgave 2:

1. Man løser to ligninger med to ubekendte (a og b) i Ti-Nspire:

   solve(1.7=a*8+b and 2.45=a*12+b,a,b) ▸ a=0.1875 and b=0.2

   Dvs. a = 0,1875 og b = 0,2

   y(x) = a·x + b oprettes som funktion i Ti-Nspire med værdierne for a og b indsat:

   y(x):=0.1875*x+0.2 ▸ Udført

   Man skal finde y(15):

   y(15) ▸ 3.0125

   Dvs. højden af flaget er 3,0 m

2. Højden af flagstangen er løsning til ligningen y(x) = 9 med hensyn til x. Løst i Ti-Nspire:

   solve(y(x)=9,x) ▸ x=46.933

   Dvs. flagstangens højde er 46,9 m

Svar på opgave 3:

1. Han købte for 1200·(113,7/104,7) kr. = 1303,15 kr.

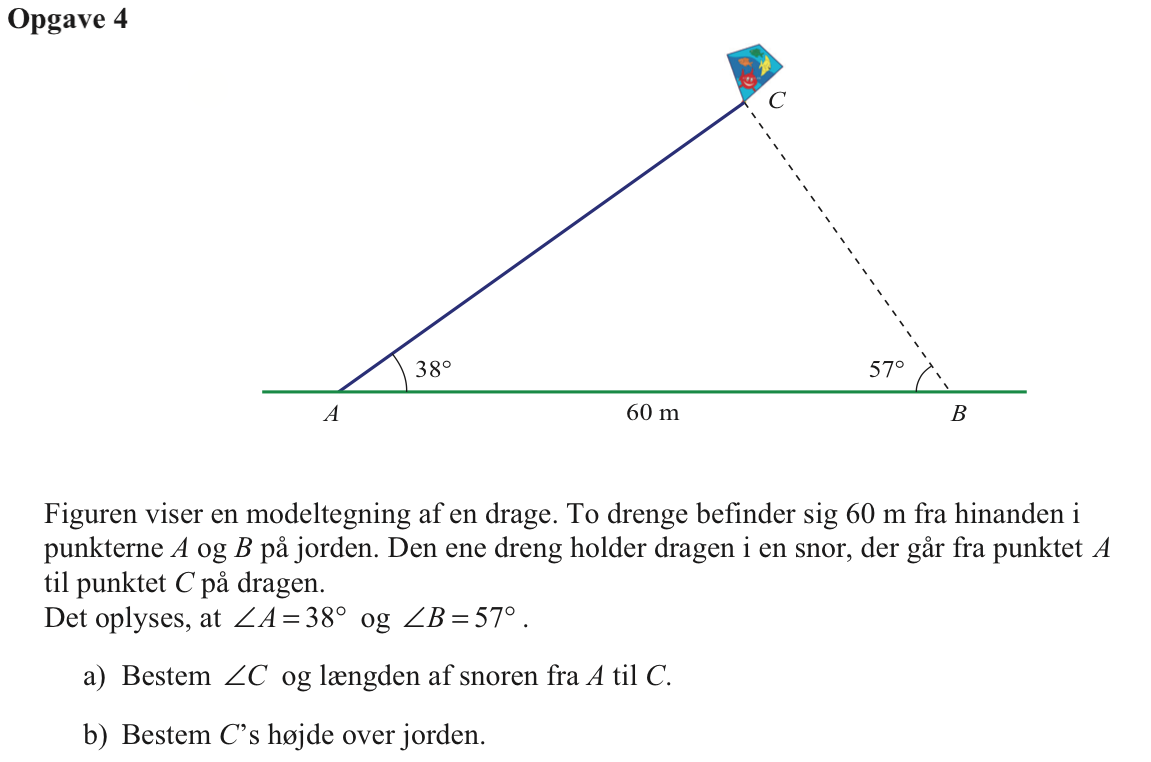
Svar på opgave 4:

1. Vinkel C findes ved hjælp af reglen om, at vinkelsummen i en trekant er 180°:

   ∠C = 180° - (38° + 57°) = 85°

   |AB| eller b findes ved hjælp af en sinusrelation i Ti-Nspire:

   solve(b/sin(57°)=60./sin(85°),b) ▸ b=50.5124

   Dvs. |AC| = 50,5 m

2. Højden fra jorden til C kaldes h_C. Der gælder at h_C = |AC|·sin(A) = 50,5124·sin(38°) m = 31,1 m

Svar på opgave 5:

1. Man opretter y(x) i Ti-Nspire:

   y(x):=0.0349*x^(3.13) ▸ Udført

   Man skal finde y(20):

   y(20) ▸ 412.14

   Dvs. fosterets vægt er 412 g

2. Man skal løse ligningen y(x) = 1200 med hensyn til x og får i Ti-Nspire:

   solve(y(x)=1200,x) ▸ x=28.139

   Dvs. fosteret er 28 uger gammelt.

Svar på opgave 6:

1. Man opretter to lister i Ti-Nspire: en med blodsukker data og en med frekvenser. Man bruger øvre grænse for blodsukker intervallerne i den første liste og tilføjer den nedre grænse af første interval som startværdi. Tilsvarende tilføjes frekvensen 0 i starten af frekvenslisten for at få sumkurven til at gå ned til første-aksen.

   blodsukker:={3,3.5,4,4.5,5,5.5,6,6.5} ▸ {3,3.5,4,4.5,5,5.5,6,6.5}

   frekvens:={0,0.06,0.18,0.28,0.18,0.1,0.12,0.08} ▸ {0,0.06,0.18,0.28,0.18,0.1,0.12,0.08}

   Man opretter dernæst en liste kaldet "kummuleret" over kummulerede frekvenser:

   kummuleret:=cumulativeSum(frekvens) ▸ {0,0.06,0.24,0.52,0.7,0.8,0.92,1.}

   I Ti-Nspires diagrammodul tegnes en sumkurve ud fra blodsukkerlisten og listen over kummulerede frekvenser:

   

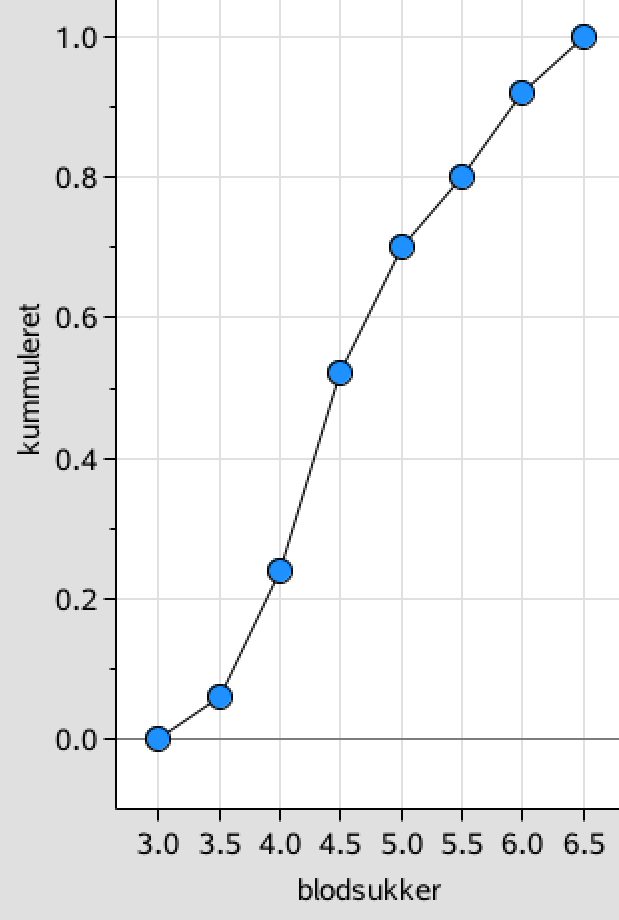
2. Øvre kvartil aflæses til 5,25 ud fra de røde linjer i nedenstående figur:

   

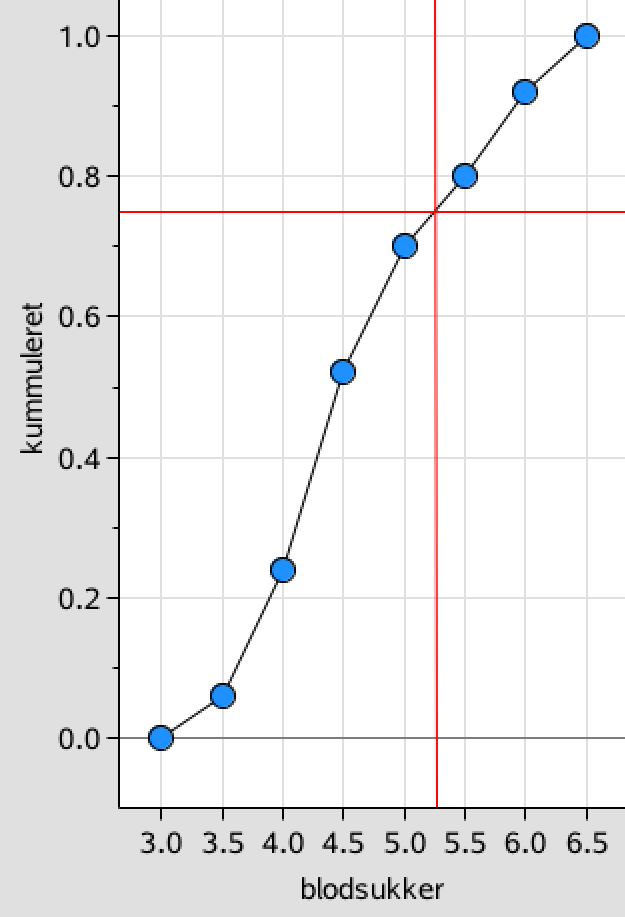
   Den vandrette linje går gennem 75 % på anden-aksen og skærer sumkurven i punktet (5,25;75 %). De 5,25 findes ved at trække en lodret linje fra skæringspunktet ned til første-aksen.

   Den øvre kvartil viser, at 25 % af de undersøgte personer har en blodsukker­koncentration på 5,25 millimol/liter eller mere

3. Middeltallet findes som summen af intervalmidtpunkt gange frekvens for interval:

   3,25·0,06 + 3,75·0,18 + 4,25·0,28 + 4,75·0,18 + 5,25·0,1 + 5,75·0,12 + 6,25·0,08 = 4,63

Svar på opgave 7:

1. Modellen er f(x) = 109·1,14^x,

   hvor f(x) er antal millioner mobilabonnenter, x er antallet af år efter 2000, 109 er antal millioner abonnenter i år 2000 og 1,14 er fremskrivningsfaktoren, dvs. 1 + den årlige tilvækst i %.

2. Fordoblingstiden er ln(2)/ln(a) = ln(2)/ln(1,14) år = 5,29 år

3. Man skal finde f(2010-2000) = f(10) = 404,087, dvs. antallet af mobilabonnementer i år 2010 er 404 millioner. Dette er større end det faktiske tal.