Svar på opgave 1:

1. Der står: (30.000 kr.)·(1 + 2,125%)⁷ = 34.757 kr.

Svar på opgave 2:

Funktionen defineres i Ti-Nspire: y(d):=0.31*d^2.11 → Udført

1. Man løser y(d=15) i Ti-Nspire: y(15) → 93.95. Svaret er: det vejer 94,0 kg

2. Det er 2^2,11 = 4,3 gange større

   Bemærk forskellen mellem:...

   1) "...hvor mange % er det større?" (som giver: [(1 + 100%)^2,11 -1]·100% = 332%) og

   2) "...hvor mange gange er det større?" (som giver: 2^2,11 = 4,3).

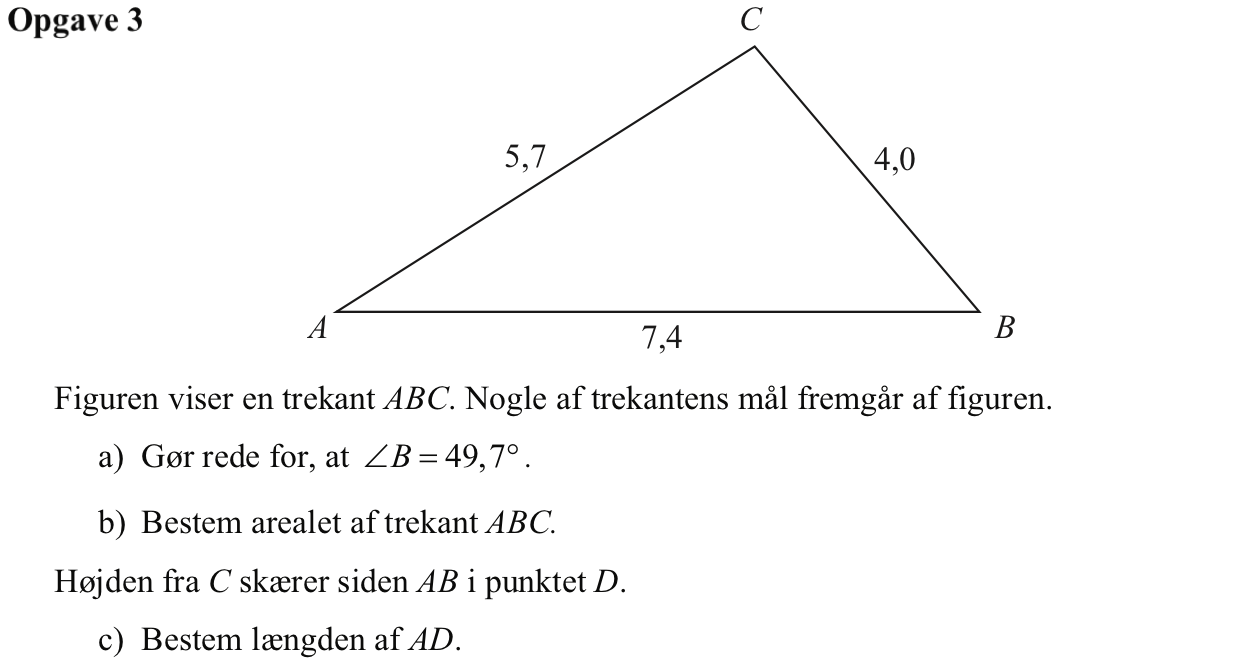
Svar på opgave 3:

1. Vinklen beregnes ved hjælp af cosinusrealtionen i Ti-Nspire, idet vinkel B kaldes x:

   

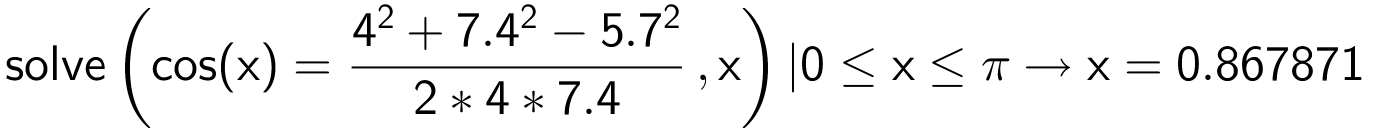
   Dette er vinkel B i radianer. Tallet omregnes til grader: 0,867871·180/π = 49,7°

Som hjælp til delopgave b) og c) laves følgende tegning i Geogebra :



2. Arealet er en halv grundlinje gange højde = 0,5·7,4·[4,0·sin(49,72°)] = 11.29

3. |AD| er 7,4 minus |DB| = 7,4 - [4,0·cos(49,72°)] = 4.81

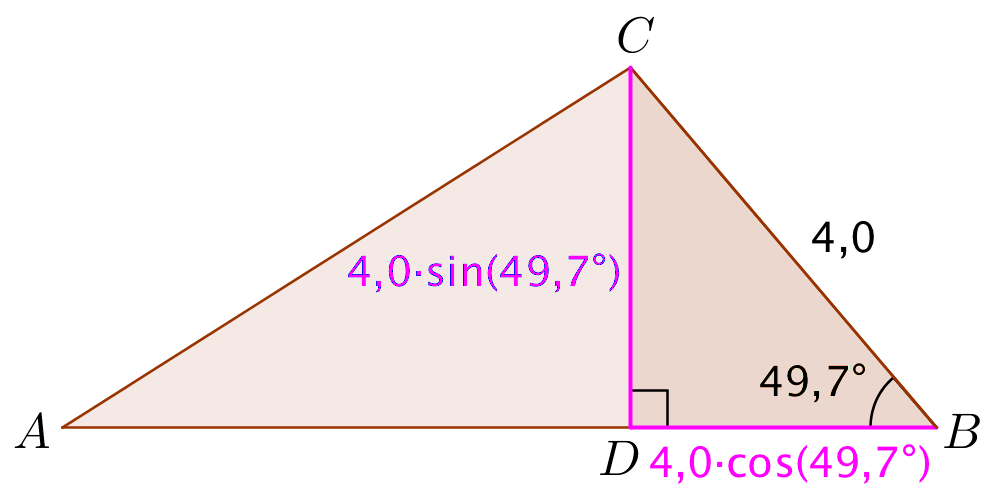
Svar på opgave 4:

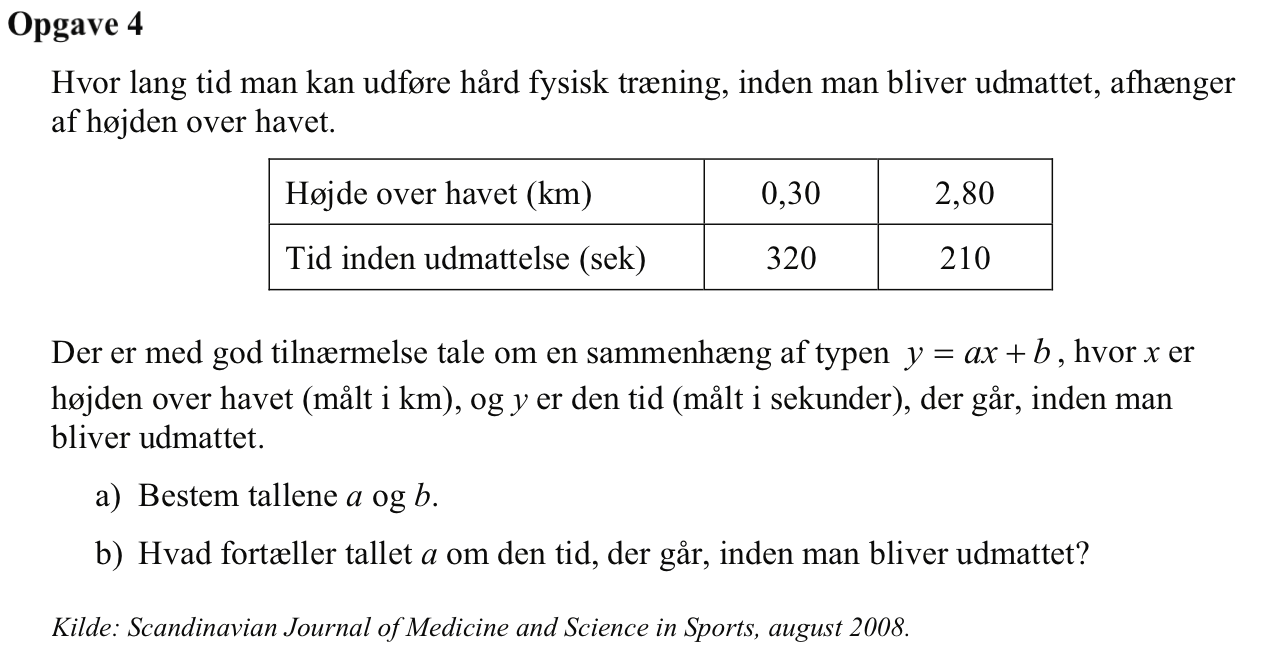
1. Man skal løse to ligninger med to ubekendte med hensyn til a og b, hvor tallene fra tabellen indsættes i stedet for x og y. Man får følgende i Ti-Nspire:

   

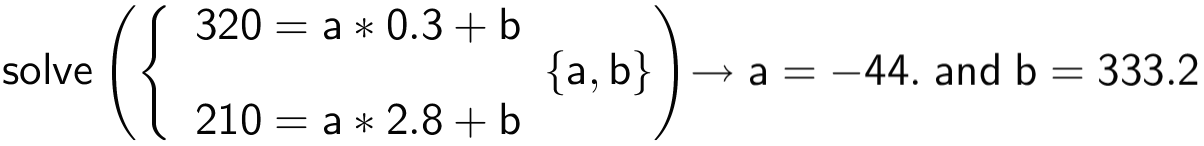
2. Tallet a (-44 sekunder) fortæller, at hver gang man stiger en kilometer, bliver man udmattet på 44 sekunder kortere tid.

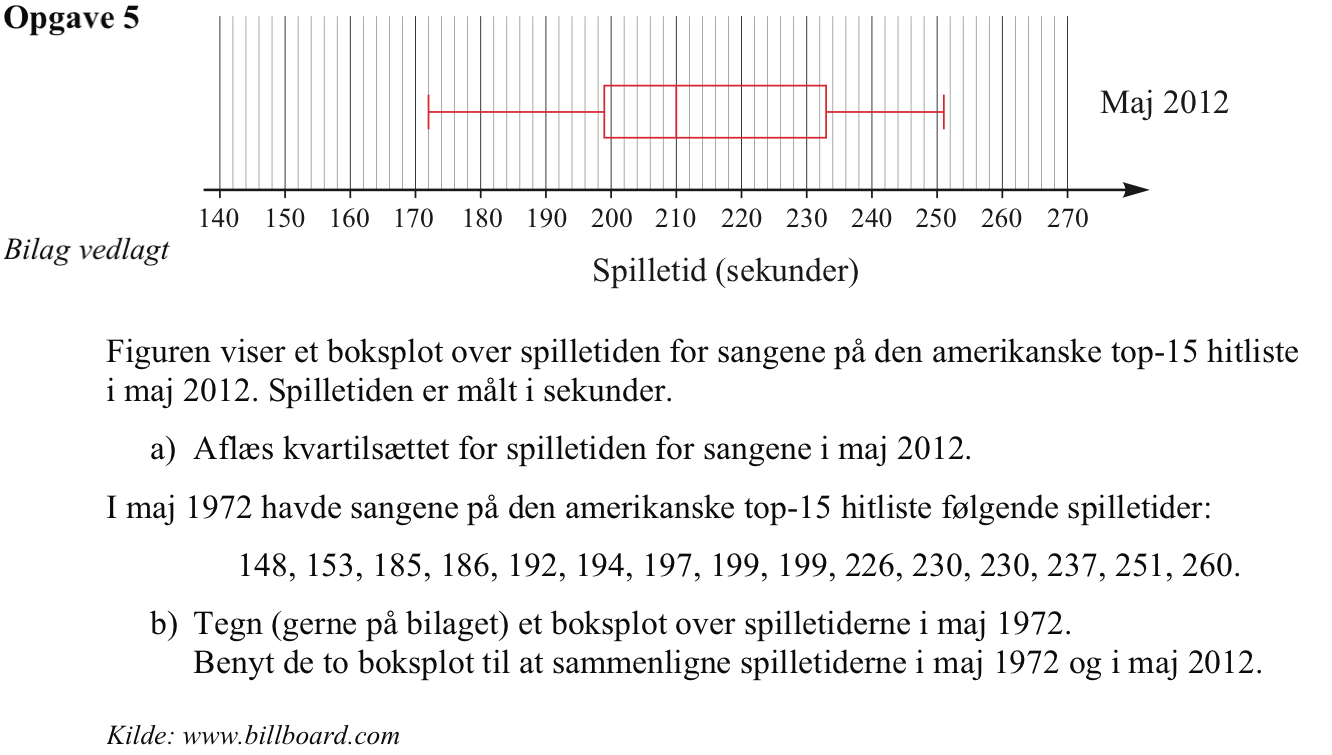
Svar på opgave 5:

1. Kvartilsættet aflæses til: Q1 = 25%-kvartilen = 199, medianen = 210 og Q3 = 75%-kvartilen = 233

2. Man laver boksplottet i Geogebra:

   

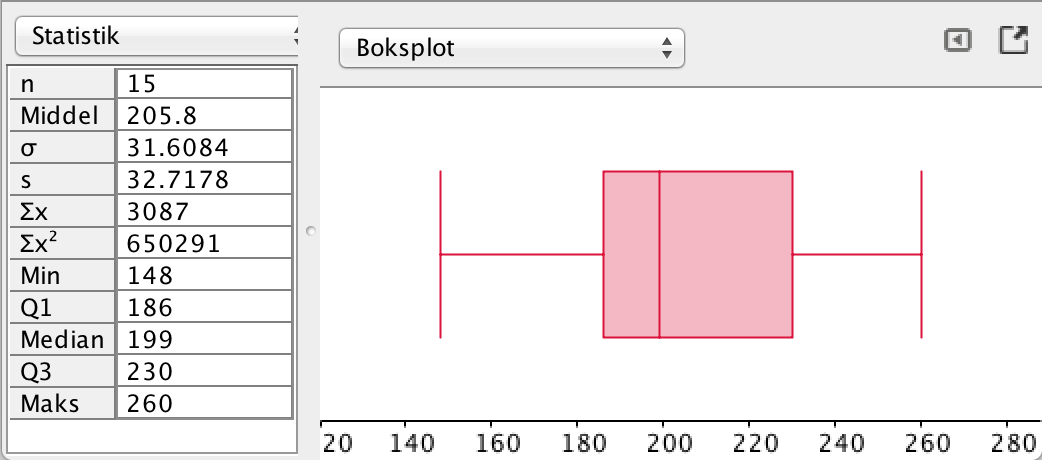
   Det ses, at Q1, median og Q3 er mindre end for 2002. Der var større variationsbredde i 1972: 148 - 260, hvor den i 2002 var 172 - 251.

Svar på opgave 6:

1. Da der er en fast årlig procentuel vækst, er der tale om eksponential vækst. Startværdien er 192 mio. Man får modellen:

   f(x) = 192·(1 + 1,3%)^x = 192·(1,013)^x, hvor x er antal år efter 2010 og f(x) er forbrug i mio. liter.

2. Man skal løse f(x) = 200 med hensyn til x. Det gøres i Ti-Nspire:

   f(x):=192*(1.013)^x → Udført

   solve(f(x)=200,x) → x=3.16

   Året, hvor man når op på 200 mio. liter er 2010 + 3 = 2013

Svar på opgave 7:

1. Indeks 2007: 100. Indeks 2012: (1254/1074)·100 = 116,8

2. For at kunne ammenligne SU med charterrejser omregner man charterejse-indekset, så det har basisår i 2007:

   Indeks 2007: 100. Indeks 2012: (132,3/114,1)·100 = 116,0. Det viser, at SU er steget mest