Svar på opgave 1:

1. Man indsætter x = 2001 - 1995 i formlen: 726·1,115^2001-1995 = 1.395 mia. USD

2. 726 er startværdien, dvs. Kinas BNP målt i mia. USD i 1995 (som er det år, hvor x = 0). 1,115 er fremskrivningsfaktoren, dvs. det tal som man skal gange sidste års tal med for at få det nye års. Fremskrivningsfaktoren minus een er lig med den årlige vækstrate.

3. Fordoblingskonstanten er ln(2)/ln(1,115) år = 6,37 år

Svar på opgave 2:

1. Kvartilsætte består af nedre kvartil, median og øvre kvartil.

   Medianen findes først. Da antallet af målinger er et lige tal, skal man tage gennemsnittet af de to midterste tal, når tallene er opstillet i nummerorden: median = (207+207)/2 = 207

   Man finder nu nedre kvartil. Det er her gennemsnittet af de to midterste tal af den første halvdel af tallene opstillet i nummerorden:

   Nedre kvartil = (198 + 198)/2 = 198

   Øvre kvartil findes tilsvarende: (232+235)/2 = 233,5

   Dvs. kvartilsættet er {198;207;233,5}

2. Resultaterne for skole B er lavere end for skole A. Medianen på 191 er lavere end for skole A, den mindte værdi på 181 er lavere end den mindste værdi for skole A og den største værdi for skole B på 219 er også lavere end den største værdi for skole A.

Svar på opgave 3:

1. Formlen er: f(x) = 45x + 4.775, hvor f(x) er samlede udgifter i kr. og x er antal trykte eksemplarer af bogen.

2. Man skal løse ligningen: 45x + 4775 = 14000 med hensyn til x:

   solve(45*x+4775=14000,x) ▸ x=205

   Dvs. antallet af trykte bøger er 205 stk., når de samlede omskostnger er 14.000 kr.

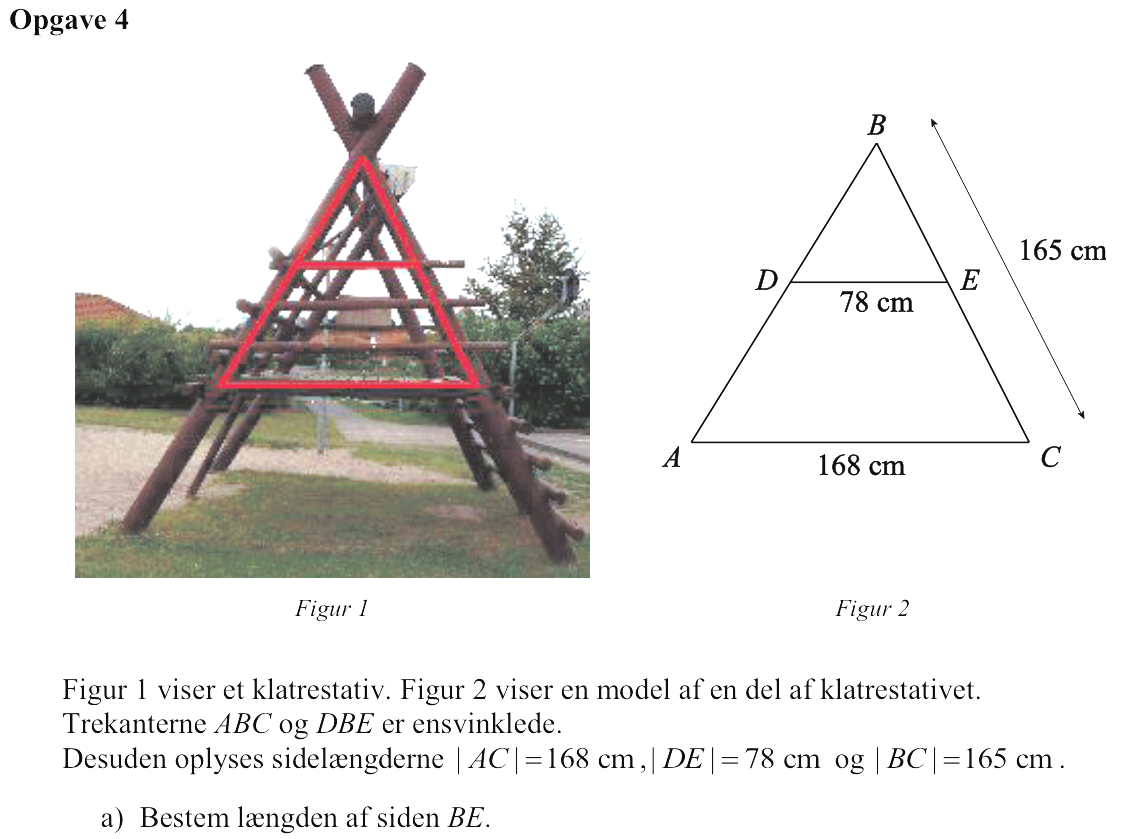
Svar på opgave 4:

1. For de ensvinklede trekanter gælder ligningen: (165 cm)/(168 cm) = |BE|/(78 cm) ⇒ |BE| = 76,6 cm

Svar på opgave 5:

1. Man skal løse de to sammenhørende ligninger: 48 = b·0,45a og 322 = b·0,85a med hensyn til a og b. Dette gøres i Ti-NSpire:

   solve(48=b*(0.45)^a and 322=b*(0.85)^a,a,b) ▸ a=2.9927 and b=523.71

   Dvs. a = 3,0 og b = 524

2. Rumfanget er 523,7·0,65^3,0 = 144,4 m²

3. Formlen for procent-procent vækst, der gælder for potensfunktioner, giver: (1,40^3,0 - 1)·100 % = 173,5 %.

   Dvs. den store bold er 173 % større end den lille.

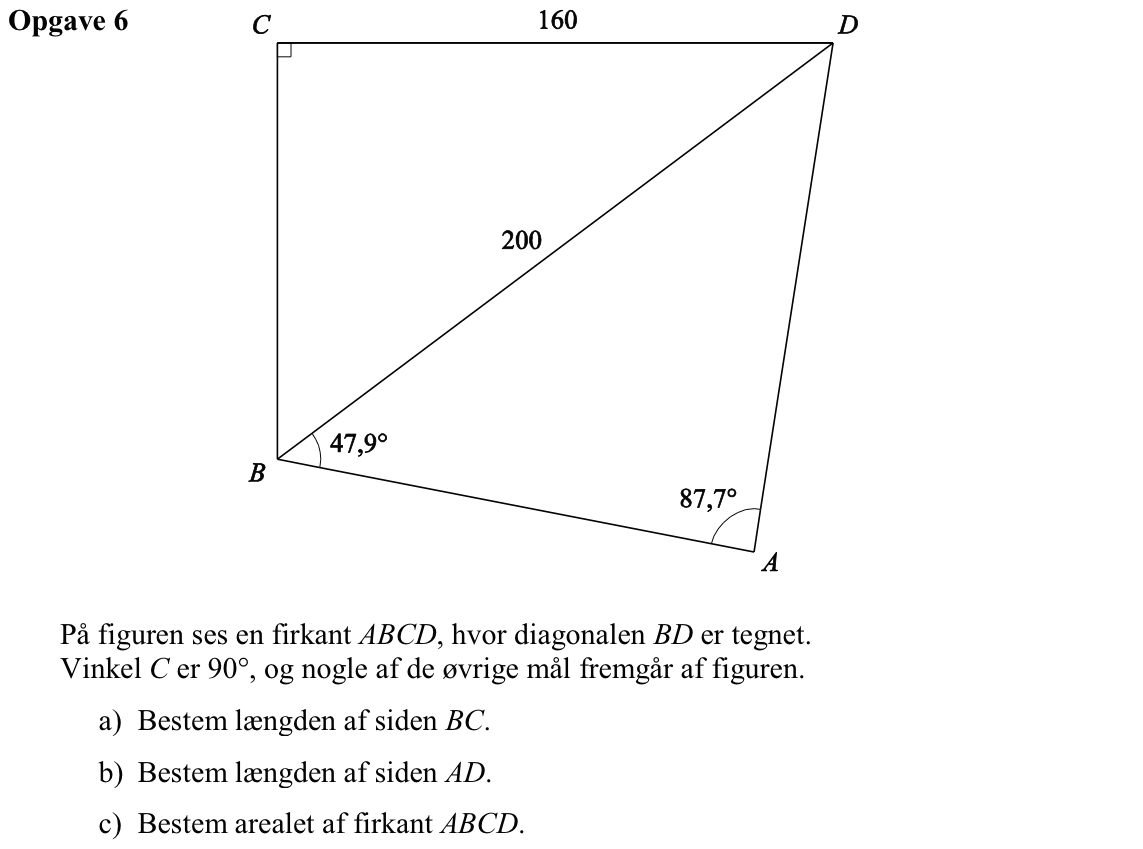
Svar på opgave 6:

1. |BC| findes ved hjælp af Pythagoras læresætning: |BC| = √[200²-160²] = 120

2. Man bruger en sinusrelation. Det gøres i Ti-Nspire: solve(200/sin(87.7°)=ad/sin(47.9°),ad) ▸ ad=148.51.

   Dvs. |AD| = 148,5 m

3. Arealet af firkant ABCD er summen af arealerne af trekant ABD og trekant BCD.

   Arealet af trekant ABD = 0,5·grundlinje·højde = 0,5·200·|AD|·sin(vinkel-D) =

   0,5·200·148,5·sin(180°-47,9°-87,7°) = 0,5·200·148,5·sin(44,4°) = 10390 m²

   Arealet er trekant BCD er 0,5·120·160 = 9600 m²

   Dvs. arealet af firkant ABCD er (10.390 + 9.600) m² = 19.990 m²

Svar på opgave 7:

1. Frysepunktet findes ved at indsætte x = 33 i formlen: -(36·33)/(100 - 33) °C = -17,7 °C

   (Hvorfor ikke x = 33 %? Fordi: x = alkoholprocenten og alkoholprocenten = 33, dermed er x = 33.)