Svar på opgave 1:

1. Efter 6 år står der: (55.620 kr.)·(1 + 1,2%)⁶ = (55.620 kr.)·(1,012)⁶ = 59.747 kr. på kontoen.

2. Man skal løse ligningen 55620·(1,012)^x = 63000 med hensyn til x. Man får i Ti-Nspire: solve(55620*(1+(1.2)%)^x=63000,x) ▸ x=10.445

   Dvs. der går 11 år før, der står 63.000 kr. på kontoen

   (Kontrol. 10 år: beløb = 55620·(1,012)¹⁰ = 62667. 11 år: beløb = 55620·(1,012)¹¹ = 63419.)

Svar på opgave 2:

1. For at finde a og b skal man løse de to sammenhørende ligninger: 2300 = 40·a + b og 3300 = 62·a + b. Det gøres i Ti-NSpire:

   solve(2300=40*a+b and 3300.=62*a+b,a,b) ▸ a=45.4545 and b=481.818

   Dvs. a = 45,45 og b = 481,8

2. Man indsætter 55 i formlen og får: (45,4545·55 + 481,818) meter = 2981,8 meter, som er den distance, som han har løbet.

3. For at finde den ekstra distance skal man løse ligningen: 45,45·(55 + x) + 481,8 = 2982 + 450 med hensyn til x. Man får i TI-Nspire:

   solve(45.45*(55+x)+481.8=2982+450,x) ▸ x=9.91089

   Dvs. han får et kondital, som er 9,9 højere

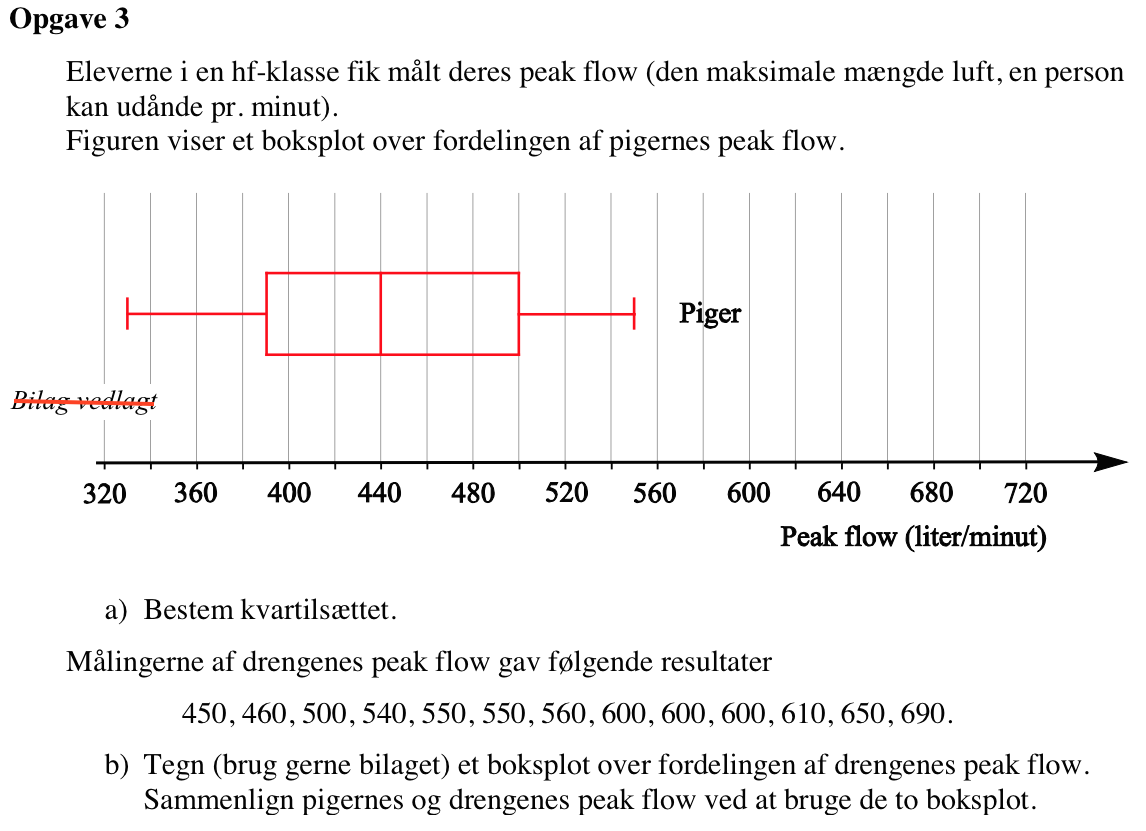
Svar på opgave 3:

1. Kvartilsættet aflæses af boksplotet. Man får: {nedre kvartil,median,øvre kvartil} = {390,440,500}

2. Man opretter en liste for drengenes peak flow i Ti-Nspire: drenge_peak_flow:={450,460,500,540,550,560,600,600,610,650,690} ▸ {450,460,500,540,550,560,600,600,610,650,690}

   Dette bruges til at lave følgende boksplot:

   

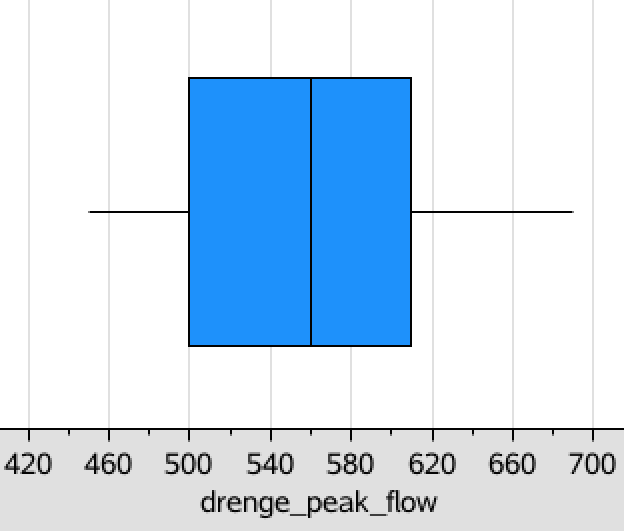
   Af boksplottet ses, at drengene har kvartilsættet: {nedre kvartil,median,øvre kvartil} = {500,560,610}. Grænserne for drengenes kvartilsæt er højere end for pigernes, dvs. drengene har generelt et højere peak flow.

Svar på opgave 4:

1. Man indsætter x = 100 i formlen for y og får: y(100) = 0,0635·100^0,822 g = 2,80 g, som er vægten af hjernen på et dyr, der vejer 100 g.

2. For at finde vægten af et dyr, hvis hjerne vejer 75 g, skal man løse ligningen: 0,0635·x^0,822 = 75 med hensyn til x. Man får følgende i Ti-Nspire: solve(y(x)=75,x) ▸ x=5464.82.

   Dvs. dyret vejer 5465 g

3. Man bruger formlen for procent-procentvækst for potensfunktioner og får: (1,25^0,822 - 1)·100 % = 20,1 %,

   som der det antal procent, som det store dyrs hjerne er tungere end det lille dyrs.

Svar på opgave 5:

1. Der gælder, antal familier divideret med indekstallet for samme år skal være konstant for alle årene. Dette giver ligningen for indekstallet for 2003 (som kaldes x): 1,54/100 = 1,9/x ⇒ x = 123,4. Dvs. indekstallet for 2003 er 123

   Antallet af familier i 2005 kaldes x. Man får ligningen 1,54/100 = x/140 ⇒ x = 2,16. Dvs. der var 2,16 mio. familier med mobiltelefon i 2005.

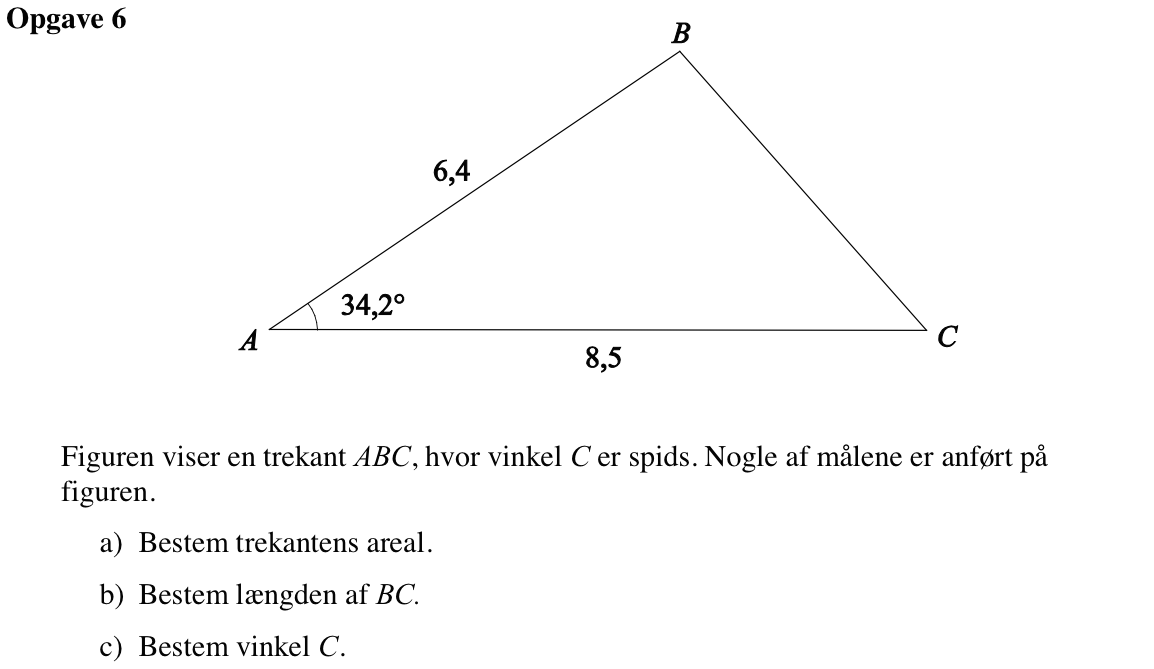
Svar på opgave 6:

1. Arealet er 0,5·grundlinje·højde = 0,5·8,5·[6,4·sin(34,2°)] = 15,29

2. Man finder |BC| ved hjælp af en cosinusrelation i Ti-Nspire:

   solve(cos(34.2°)=(6.4²+8.5²-x²)/(2*6.4*8.5),x) ▸ x=−4.81909 or x=4.81909

   Kun den positive værdi er gyldig, og man får derfor, at |BC| = 4,82

3. Man bruger en sinusrealtion i Ti-Nspire til at finde vinkel C (som man ved er spids):

   solve(sin(x*1.°)/6.4=sin(34.2°)/4.81909,x)|0<x<90 ▸ x=48.286

   Dvs. vinkel C = 48,3°

Svar på opgave 7:

1. Modellen for udviklingen i familiernes elforbrug er f(x) = 4770·(1-2%)^x = 4770·0,98^x, hvor f(x) er det årlige elforbrug i kWh, og x er antal år efter 2005.