Svar på opgave 1:

1. Kapitalen er vokset til 250000·(1+4%)⁵ kr. = 250000·(1,04)⁵ kr. = 304.163 kr.

2. Man skal løse ligningen 250000·(1+x)⁵ = 287574,5 med hensyn til x. Det gøres i Ti-Nspire: solve(250000*(1+x)⁵=287574.5,x) ▸ x=0.0284

   Dvs. den gennemsnitlige rentesats er 2,84 %

Svar på opgave 2:

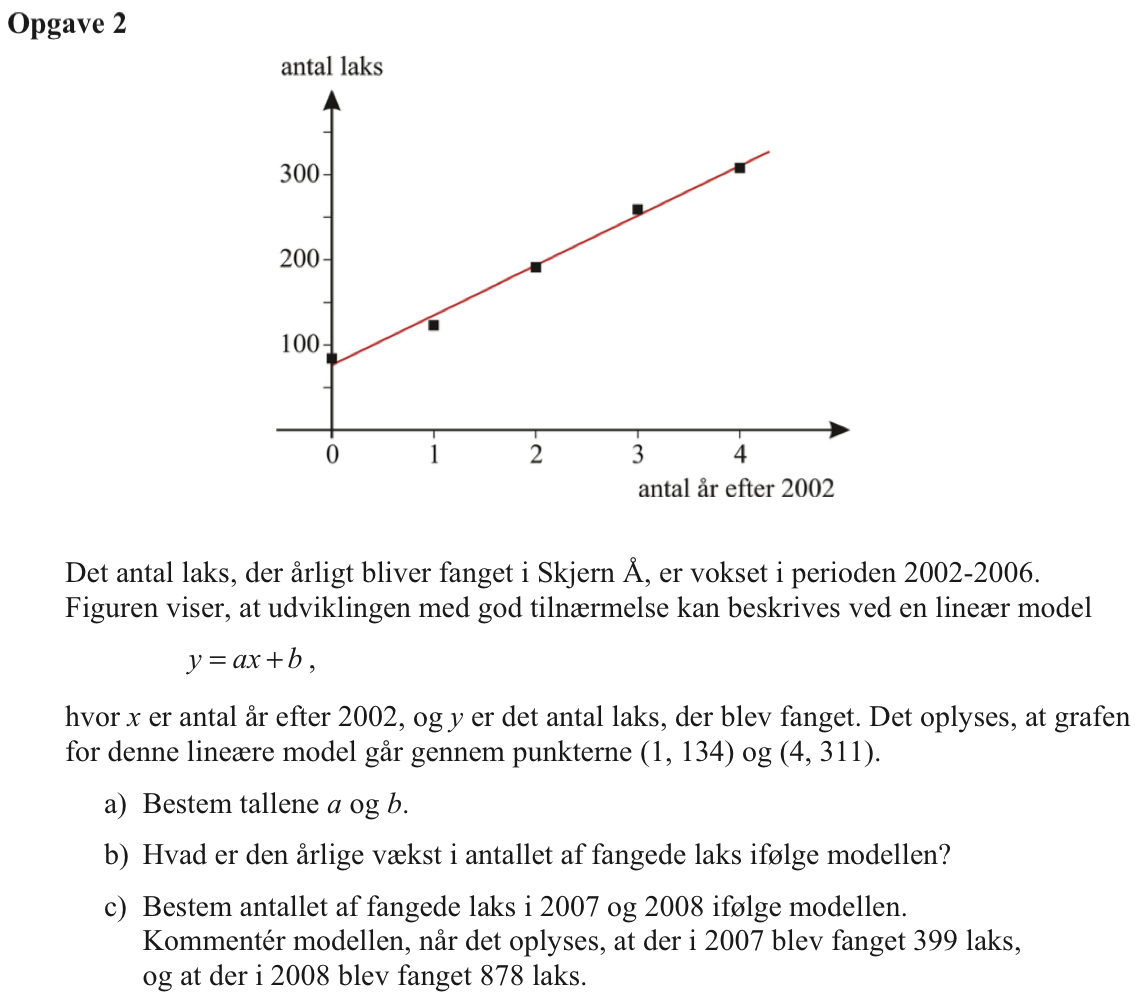
1. For at finde a og b skal man løse de to sammenhørende ligninger: 134 = a·1 + b og 311 = a·4 + b. Dette gøres i Ti-Nspire: solve(134=a*1+b and 311=a*4+b,a,b) ▸ a=59 and b=75

   Dvs. a = 59 og b = 75

2. Den årlige vækst er a, dvs. 59 laks

3. Antallet fangede laks i 2007 er 59·(2007-2002) + 75 = 370

   Antallet af fangede laks i 2008 er 59·(2008-2002) + 75 = 429

   Modellens tal for 2007 passer nogenlunde, mens tallet for 2008 er forkert.

Svar på opgave 3:

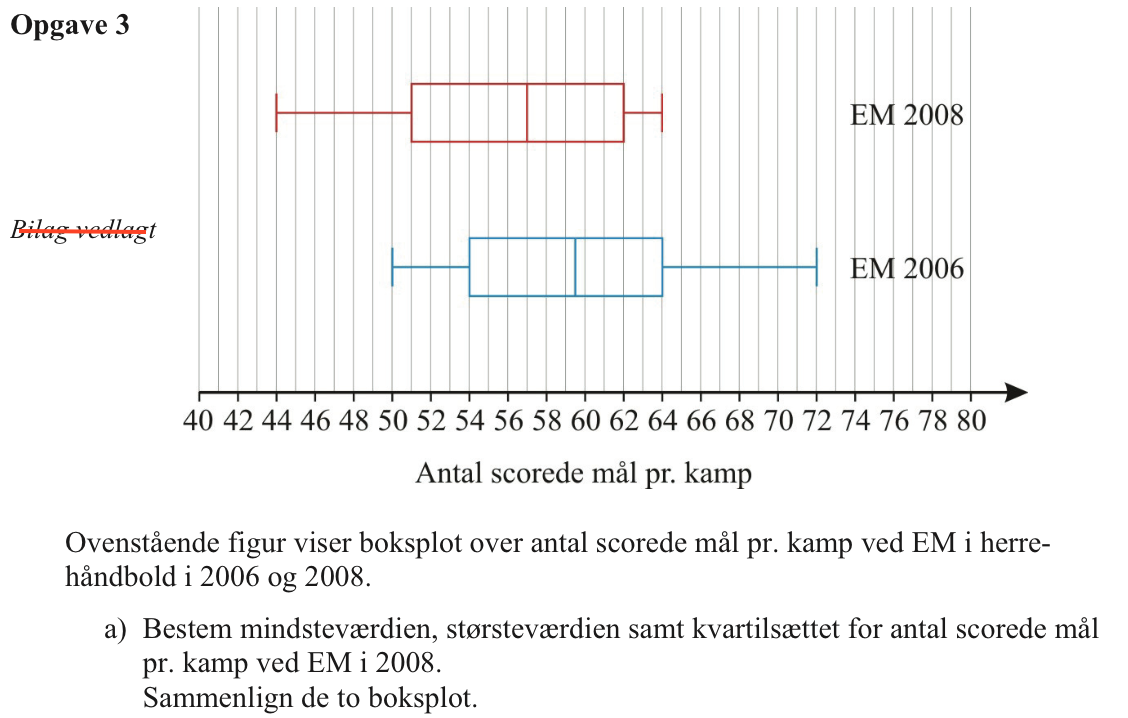
1. Mindsteværdi: 44, størsteværdi: 64, nedre kvartil: 51, median: 57 og øvre kvartil: 62.

2. Generelt blev der scoret flere mål i 2006 end i 2008.

Svar på opgave 4:

1. Man skal løse ligningen 0,25 = 0,7·0,85·d² med hensyn til d. Dette gøres i TI-NSpire: solve(0.25=0.7*0.85*d² and d>0,d) ▸ d=0.648204

   Dvs. diameteren er 0,65 m

Svar på opgave 5:

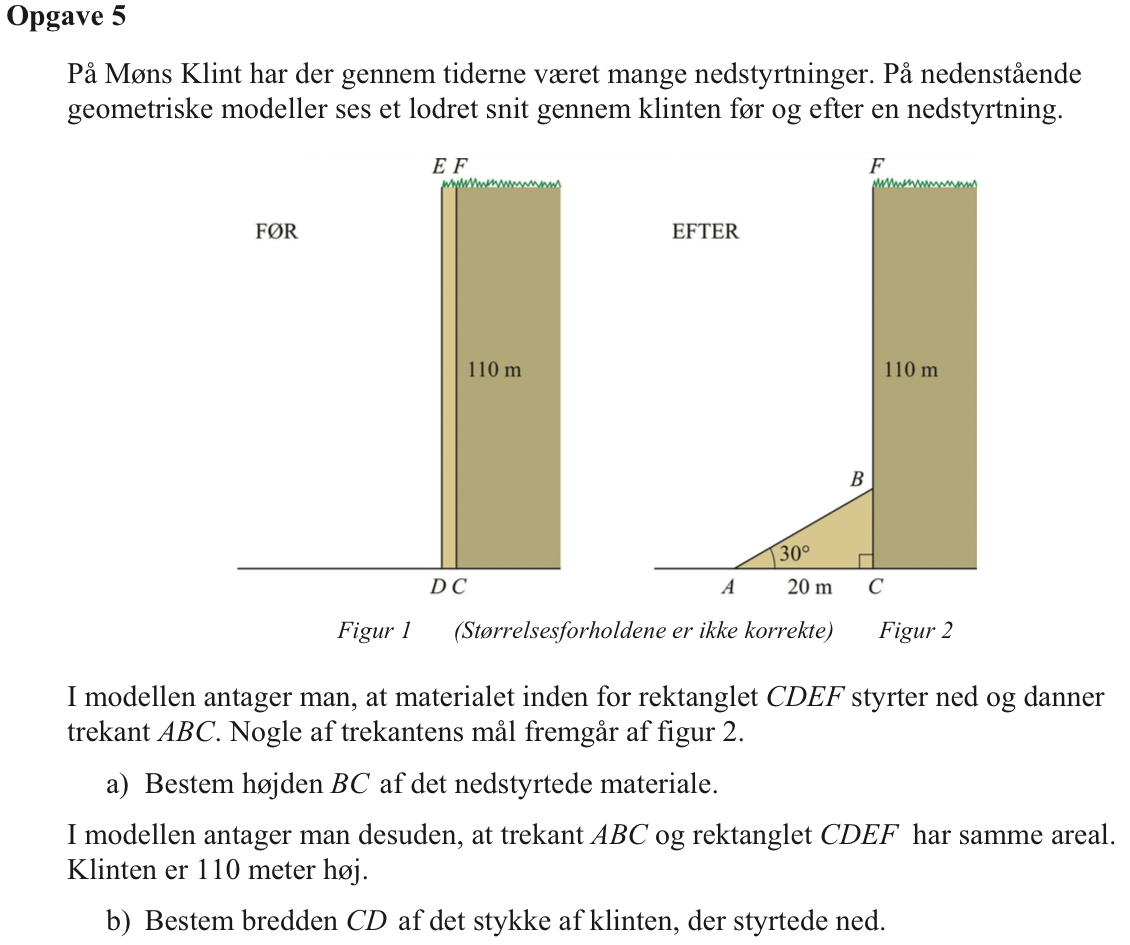
1. Der gælder den trigonometriske sammenhæng: tan(30°) = |BC|/20. Dette løses med hensyn til |BC| i Ti-Nspire: solve(tan(30.°)=bc/20,bc) ▸ bc=11.547

   Dvs. |BC| er 11,55 m

2. Der gælder sammenhængen: Areal af firkant CDEF = areal af trekant ABC. Dette giver ligningen: |CD|·110 = 0,5·20·11,547, som løses med hensyn til |CD| i Ti-Nspire: solve(cd*110=0.5*20*11.547,cd) ▸ cd=1.04973

   Dvs. |CD| = 1,05 m

Svar på opgave 6:

1. Når x og y er proportionale gælder, at x/y = konstant for alle par af x og y. Dvs. for det første tomme felt får man ligningen: x/3 = 6/9 som giver x/3 = 6/9 ⇔ x = 3·6/9 ⇔ x = 2

   For det andet felt får man: 5/y = 6/9 som giver 5/y = 6/9 ⇔ 5 = y·6/9 ⇔ y = 5/(6/9) ⇔ y = 7,5

Svar på opgave 7:

1. Modellen for udviklingen i medicinudgifterne er f(x) = 1,75·1,228^x, hvor f(x) er medicinudgifter i mia. kr. og x er antal år efter 2003.

Svar på opgave 8:

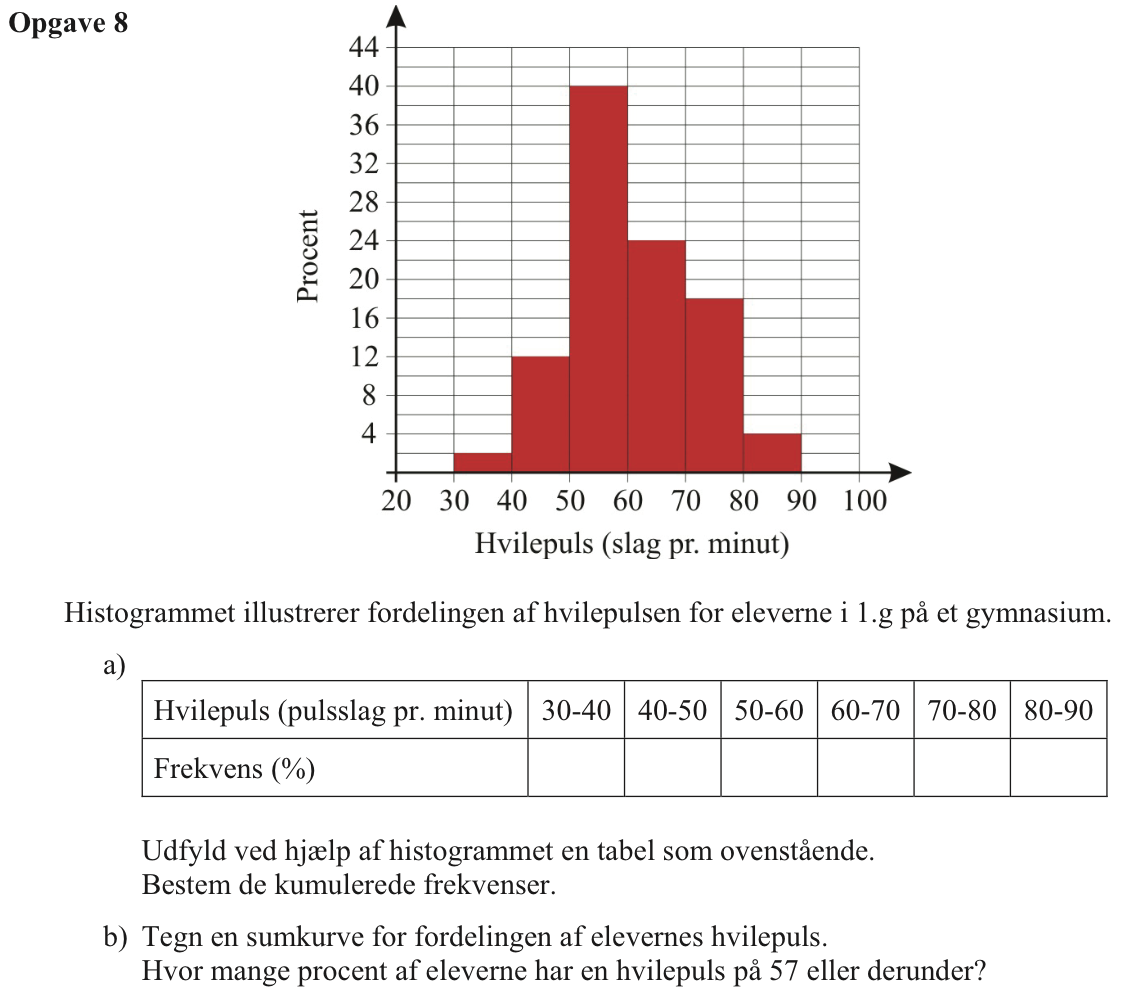
1. Man aflæser frekvenserne som højden på søjlerne: {2,12,40,24,18,4}

   Man opretter en liste for intervalgrænser for pulsen i Ti-Nspire. Man starter med nedre grænse for første interval og tilføjer derefter øvre grænse for hvert interval: puls_grænser:={30,40,50,60,70,80,90} ▸ {30,40,50,60,70,80,90}.

   Tilsvarende oprettes en liste for frekvenser, hvor nederste værdi sættes til 0: frekvens:={0,2,12,40,24,18,4} ▸ {0,2,12,40,24,18,4}. En liste med de kummulerede frekvenser oprettes til sidst: kumm_frekv:=cumulativeSum(frekvens) ▸ {0,2,14,54,78,96,100}

2. Ud fra listerne over pulsgrænser og kummulerede frekvenser tegnes sumkurven:

   

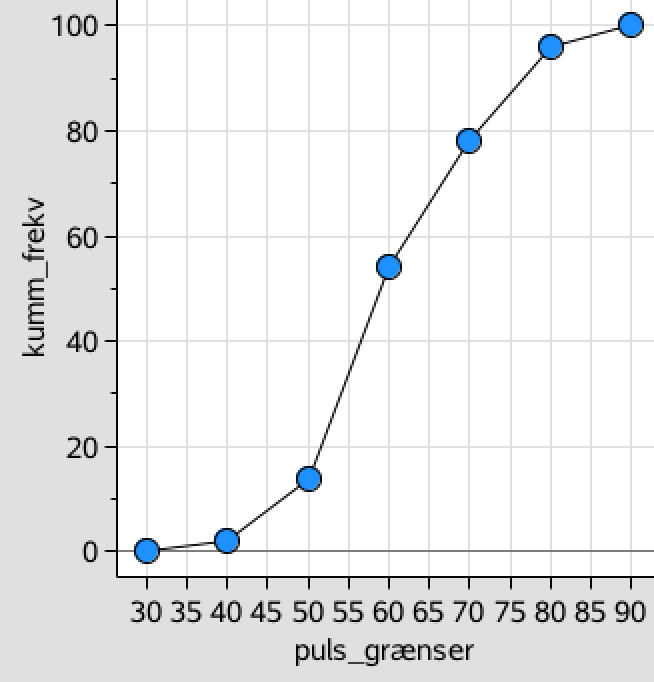
   Antal procent af elever, der har en hvilepuls på 57 eller derunder aflæses af sumkurven til 42 % som vist:

   

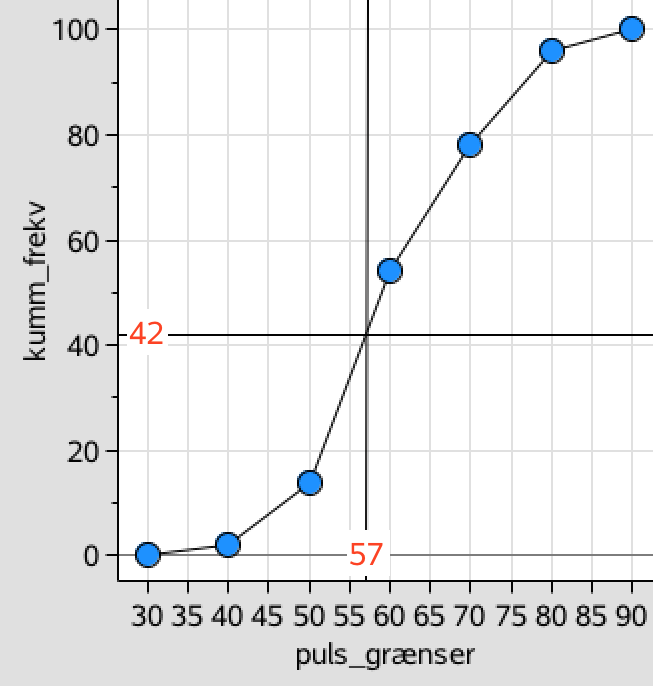
Svar på opgave 9:

1. Man sætter x = 8 ind i formlen og får: 131,8·8^-2,5 m = 0,73 m, der er afstanden mellem spærene for et tag med en bredde på 8 m.

2. Man bruger formlen for procent-procentvækst for en potensfunktion, der giver: ((1,25)^-2,5 - 1)·100 = −42,76. Dvs. afstanden mellem spærene på det brede tag på typehus A er 43 % mindre end afstanden på det smalle tag på typehus B.