
Svar på opgave 1:
-
Beløbet på kontoen efter fire år er 30000·(1+(2,3)%)4 = 32.856,70 kr.
-
For at finde det antal år, der går før beløbet på kontoen overstiger 35000 kr., skal man løse følgende lignng med hensyn til x: 30000·(1 + (2,3)%)x = 35000. Dette gøres i Ti-Nspire:
solve(30000*(1+(2.3)%)x=35000,x) ▸ x=6.77899
Man runder op og får, at der går 7 år før beløbet overstiger 35.000 kr.
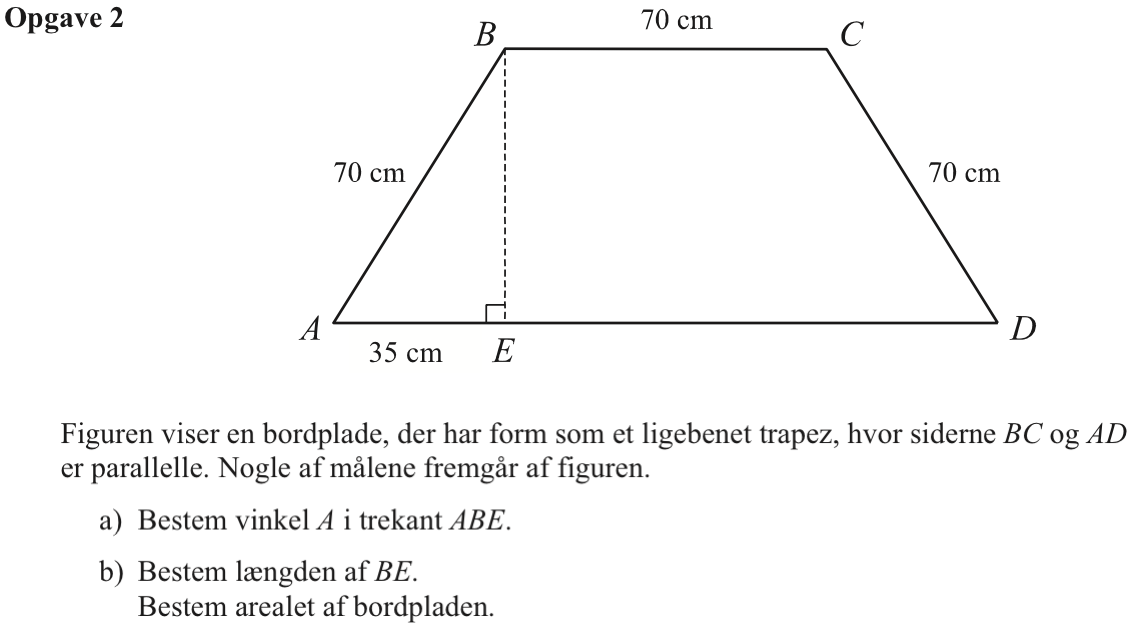
Svar på opgave 2:
-
Trekant ABE er retvinklet. Man kan finde vinkel A ved hjælp af ligningen: 70·cos(∠A) = 35, hvor det er underforstået, at ∠A er spids. Man får følgende i Ti-Nspire: solve(70*cos(x*1.°)=35,x)|0<x<90 ▸ x=60.
Dvs. vinkel A er 60°
-
|BE| kan findes ved hjælp af Pythagoras læresætning: solve(be2+352=(70.)2 and be>0,be) ▸ be=60.6218
Dvs. |BE| = 60,6
(Man kan også bruge: 70·sin(60°) = 60,62)
Da trapezen er ligebenet, får man som vist på nedenstående tegning, at den længste parallelle side er 2·35 cm + 70 cm = 140 cm.
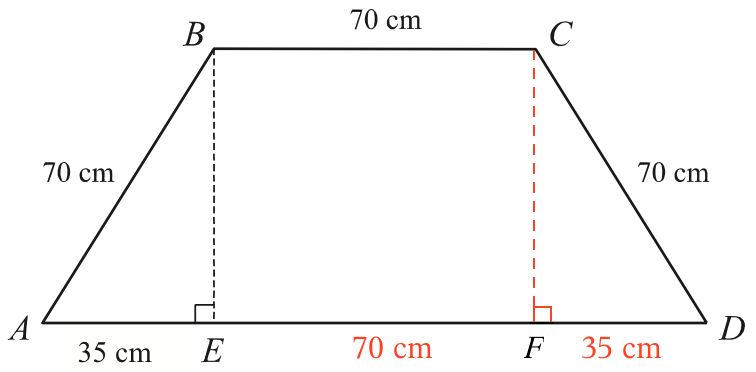
Det giver arealet: 60,62·(140 + 70)/2 = 6365,3

Svar på opgave 3:
-
Formlen er: f(x) = (34,15·x + 581,25) kr.,
hvor f(x) er den samlede årlige udgift til vand, når man bor i Holstebro og x er antal kubikmeter vand, som man bruger om året.
-
I Holstebro koster et årligt forbrug på 12 m3 vand: (34,15·12 + 581,25) kr. = 991,05 kr.
I Hillerød koster et årligt forbrug på 12 m3 vand: (49,38·12 + 308,75) kr. = 901,31 kr.
For at finde det antal kubikmeter vand der skal bruges før prisen i Hillerød overstiger prisen i Holstebro, skal man løse ligningen: 34,15·x + 581,25 = 49,38·x + 308,75 med hensyn til x.
Dette gøres i TI-Nspire: solve(34.15*x+581.25=49.38*x+308.75,x) ▸ x=17.8923
Dvs. forbruget skal være 17,9 m3

Svar på opgave 4:
-
Man finder den årlige produktion ved at indsætte x = 50 i formlen for E. Man får: 0,14·502 kWh = 350 kWh
-
For at finde vingelængde, skal man løse ligningen 0,14·x2 = 600 med hensyn til x. Dette gøres i Ti-Nspire: solve(0.14*x2=600 and x>0,x) ▸ x=65.465
Dvs. vingelængden skal være 65,5 cm
-
Man bruger formlen for procent-procentvækst for potensfunktioner: (1,252 - 1)·100 % = 56,25 %, der er det antal procent, som den nye vindmølles årlige produktion er større end den gamle.
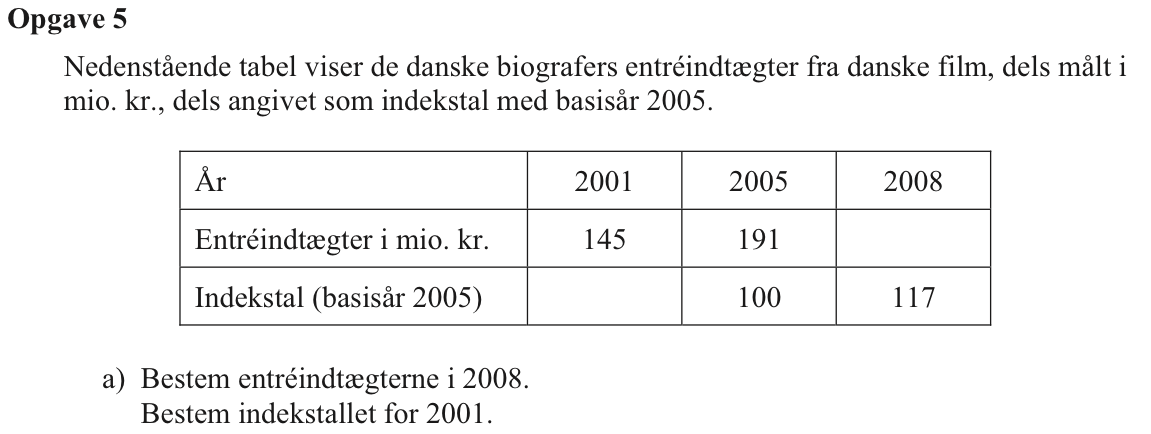
Svar på opgave 5:
-
Der gælder, at forholdet indtægt/indeks for et bestemt år er ens for alle år. Det giver
2008: indtægt/117 = 191/100 mio. kr. ⇒ 117·191/100 mio. kr. ⇒ indtægt = 223,5 mio. kr.
2001: 145/index = 191/100 ⇒ index = 145/(191/100) ⇒ index = 75,9
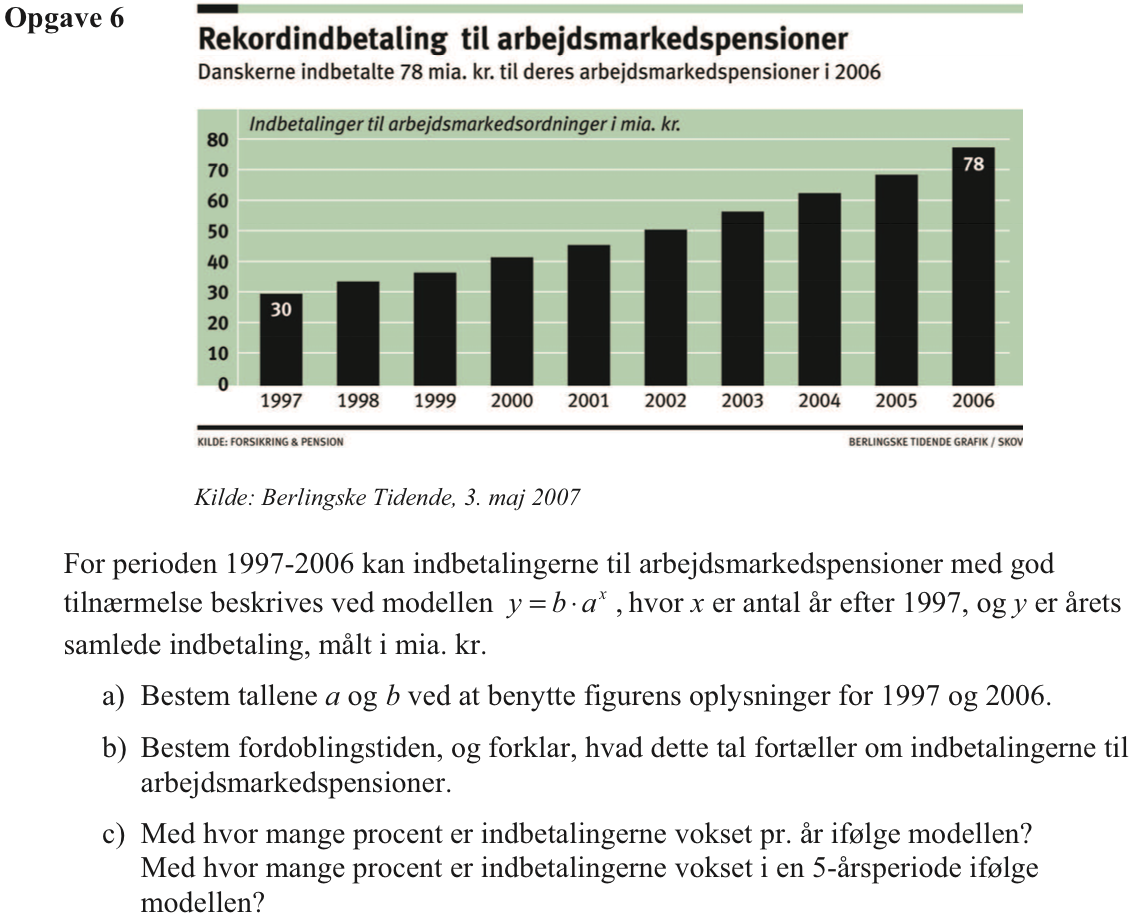
Svar på opgave 6:
-
For at finde a og b skal man løse de sammenhængende ligninger b·a0 = 30 og b·a9 = 78. Disse løses i Ti-Nspire: solve(b*a0=30 and b*a9=78.,a,b) ▸ a=1.11201 and b=30.
Dvs. a = 1,112 og b = 30
-
Fordoblingstiden er ln(2)/ln(1,112) = 6,53, som er det antal år, der går før mængden af indbetalinger er fordoblet.
-
Den årlige vækstrate, som der spørges om, er: (a - 1) = 11,2 %
Over 5 år bliver den samlede vækst i procent: ((1,112)5 - 1)·100 % = 70,0 %
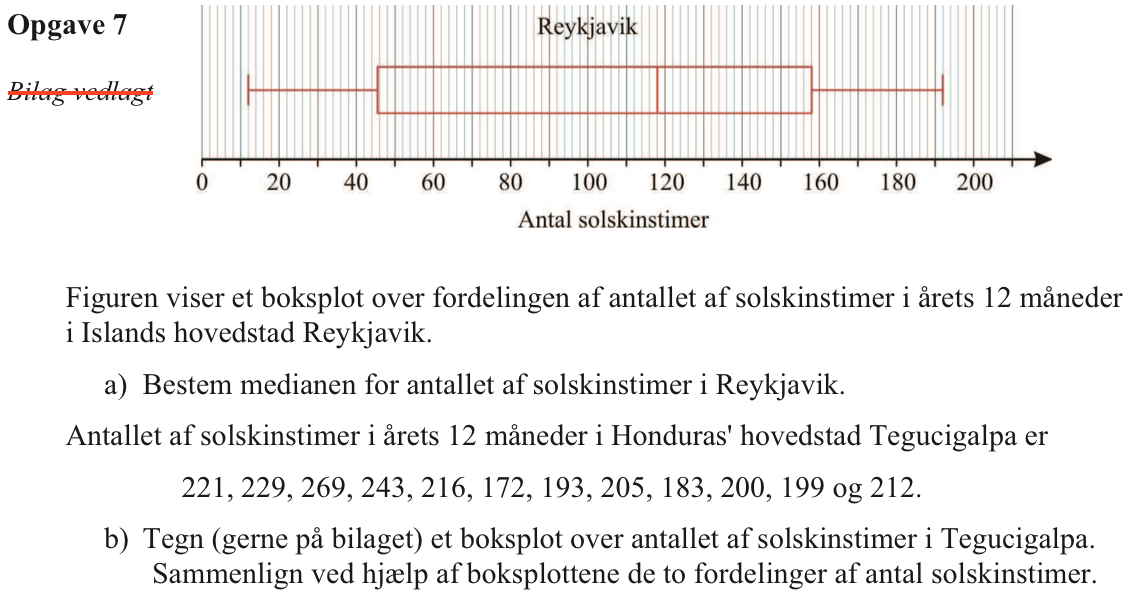
Svar på opgave 7:
-
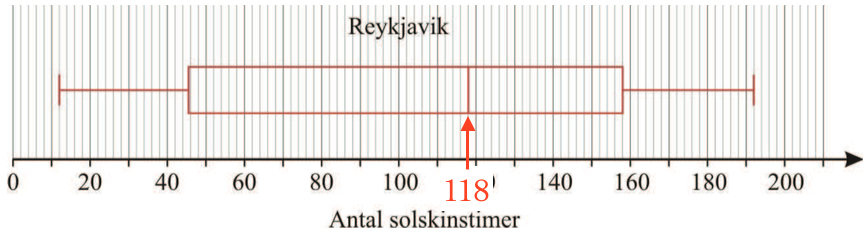
Medianen for antal solskinstimer på en måned ved Reykjavik aflæses til 118 timer som vist på figuren nedenunder:
-
Antallet af solskinstimer oprettes som en liste i Ti-NSpire, som derefter sorteres. Det færdige resultat er: solskin_honduras ▸ {172,183,193,199,200,205,212,216,221,229,243,269}
(Sorteringen foretages med kommandoen SortA solskin_honduras ▸ Udført, der virker tilbage på den opringelige liste, når man er i Noter.)
Man får følgende boksplot i Ti-Nspire:
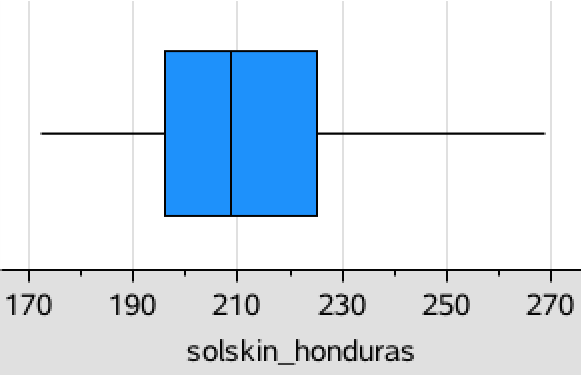
Grænserne for boksplottet for Tegucigalpa ligger generelt højere end for Reykjavik, dvs. solen skinner mere det første sted end det sidste. Der er også mindre variation i det månedlige antal solskinstimer for Tegucigalpa end for Reykjavik (variationsbredden er mindre.)