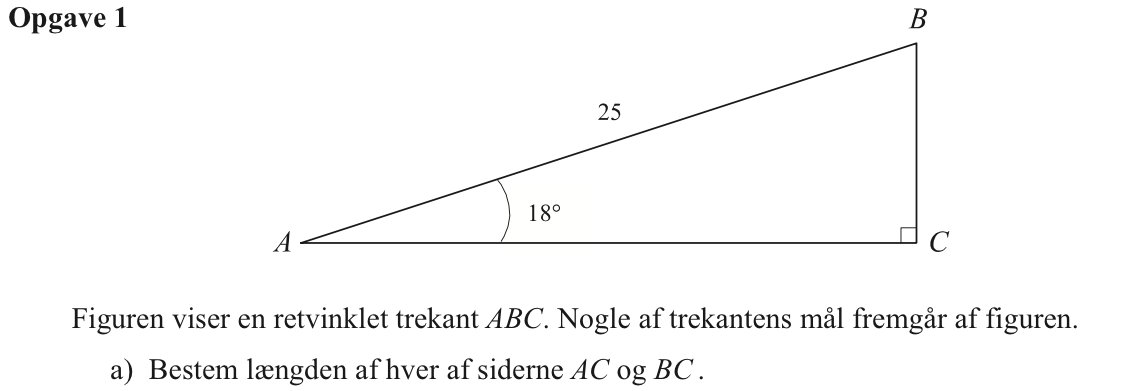
Svar på opgave 1:

1. Man benytter trigonometriske sammenhænge for retvinklerde trekanter:

   |AC| = 25·cos(18°) = 23,8 (en vinkels hosliggende katete er lig med hypotenusen gange cosinus til vinklen.)

   |BC| = 25·sin(18°) = 7,73 (en vinkels modstående katete er lig med hypotenusen gange sinus til vinklen.)

Svar på opgave 2:

1. Man skal løse ligningen: K = K₀·(1+r)ⁿ med hensyn til K₀. Dette gøres i Ti-Nspire: solve(k0*(1+(3.5)%)⁶=17332.5,k0) ▸ k0=14100.

   Dvs. det oprindelige beløb på kontoen var: 14.100 kr.

Svar på opgave 3:

1. Man skal beregne T, når x = 0,6. Man får: T = 2·(0,6)^0,5 = 1,55

2. Man anvender formlen for procent-procentvækst for en potensfunktion og får at svingningstiden øges med ((1,75)^0,5 - 1)·100 % = 32,3 %, når strengens længde øges med 75 %.

Svar på opgave 4:

1. Vinkel A findes ved hjælp af formlen: tan(A) = 2,5/8,0, som løses med hensyn til vinkel A i Ti-Nspire: solve(tan(a*1.°)=2.5/8.,a)|0<a<90 ▸ a=17.354. Dvs. vinkel A = 17,4°

2. |CD| = |AD| - |AC| = 8,0 m - |AC|. For de ensvinklede trekanter ABC og ADE gælder: |AC|/(1,5 m) = (8 m)/(2,5 m) ⇒ |AC| = 4,8 m. Det giver, at |CD| = 8 m - 4,8 m = 3,2 m

Svar på opgave 5:

1. Koncentrationen i blodet efter 24 timer er 1,8·(0,983)²⁴ = 1,193 ng/mL

   Den rate som koncentrationen ændre sig med er: (a - 1)·100 % = (0,983 - 1)·100 % = −1,7%. Dvs. koncentrationen aftager med 1,7 % i timen.

2. Man skal løse ligningen 1,8·(0,983)^x = 1. Dette gøres i Ti-Nspire: solve(1.8*(0.983)^x=1,x) ▸ x=34.281

   Dvs. der går 34,3 timer før koncentrationen kommer under 1,0 ng/mL.

Svar på opgave 6:

1. For at finde a og b skal man løse de to sammenhørende ligninger: 2270 = a·4 + b og 4820 = a·14 + b. Dette gøres i Ti-Nspire: solve(2270=a*4+b and 4820=a*14+b,a,b) ▸ a=255 and b=1250.

   Dvs. a = 255 og b = 1250

2. a er prisen pr. kubikmeter grus.

3. Man skal løse ligningen: 255·x + 1250 = 300·x + 750. Dette gøres i Ti-Nspire: solve(255*x+1250=300*x+750.,x) ▸ x=11.1111

   Dvs. man skal købe 11,1 m³ før den første vognmand er den billigste.

Svar på opgave 7:

1. Man opretter en liste over indkomstgrænser i Ti-Nspire. Man starter med første intervals nedre grænse og fortsætter derefter med øvre grænse for hvert interval. Man vælger 1.200.000 som øvre grænse.

   indkomst:={0,200000,400000,600000,800000,1000000,1200000} ▸ {0,200000,400000,600000,800000,1000000,1200000}

   Man opretter en liste i Ti-Nspire over frekvenser og tilføjer 0 som første element svarende til nedre indkomstgrænse.

   frekvens:={0,4,24,29,24,10,9} ▸ {0,4,24,29,24,10,9}

   Man bruger kommandoen cumulativeSum() i Ti-Nspire til at finde de kumulerede frekvenser.

   kum_frekvens:=cumulativeSum(frekvens) ▸ {0,4,28,57,81,91,100}

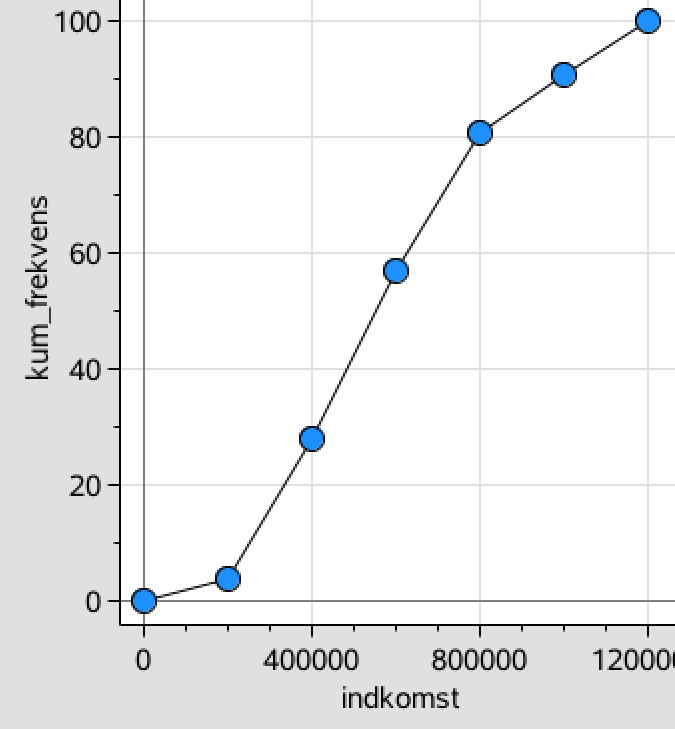
   Ud fra denne liste tegnes sumkurven:

   

2. Den nedre kvartil findes som vist på sumkurven ud fra frekvensen 25 % og aflæses på førsteaksen til 373.700.

   

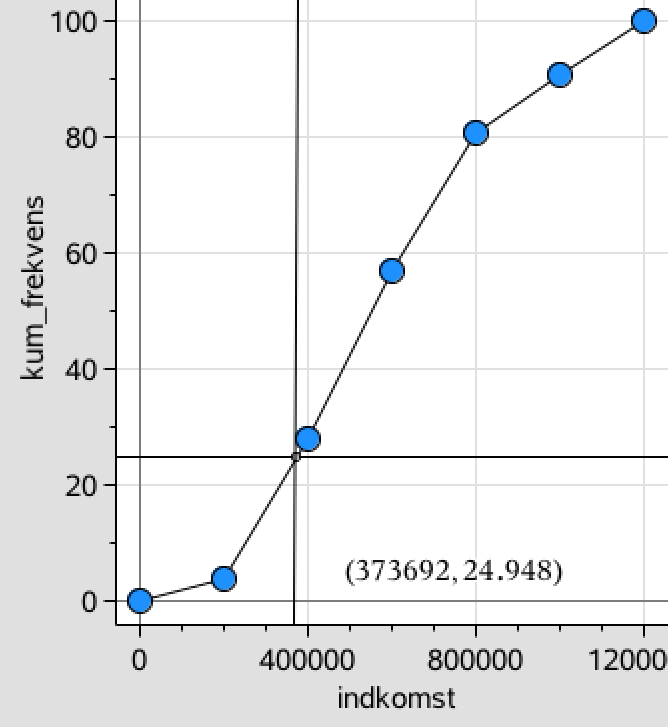
   Den nedre kvartil viser, at 25 % af de som købte bil i 2005 tjente under 373700 kr.

Svar på opgave 8:

1. At længde af streng og frekvens af tone er omvent proportionale betyder, at længde gange frekvens er konstant for alle længder. Dette giver for skemaet:

   (60 cm)·(440 Hz) = (30 cm)·frekvens ⇒ frekvens = [(60 cm)·(440 Hz)]/(30 cm) ⇒ frekvens = 880 Hz

   (60 cm)·(440 Hz) = længde·(1100 Hz) ⇒ længde = [(60 cm)·(440 Hz)]/(1100 Hz) ⇒ længde = 24 cm