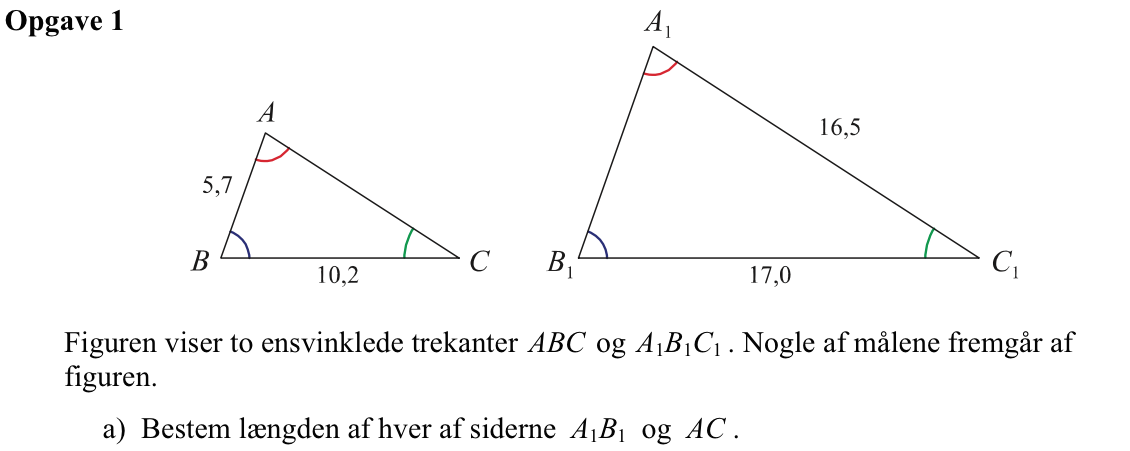
Svar på opgave 1:

1. Skaleringsfaktoren for de to ensvinklede trekanter er 17/10,2 eller 10,2/17. Man får:

   |A₁B₁| = (17/10,2)·5,7 = 9,5

   |AC| = (10,2/17)·16,5 = 9,9

Svar på opgave 2:

1. Man skal løse de to sammenhørende ligninger: (2001 - 2001)·a + b = 156000 og (2005 - 2001)·a + b = 206000. Man får følgende i Ti-Nspire:

   solve(a*0+b=156000 and a*4+b=206000,a,b) ▸ a=12500 and b=156000

   Dvs. a = 12500 og b = 156000

2. Man skal løse ligningen 12500·x + 156000 = 275000. Dette gøres i TI-Nspire:

   solve(12500*x+156000=275000.,x) ▸ x=9.52

   Man runder dette op til 10 år og får årstallet 2001 + 10 = 2011

Svar på opgave 3:

1. Man skal bruge opsparingsformlen og løse ligningen: 16593,71 = K₀·(1,0204)⁵ med hensyn til K₀. Dette gøres i Ti-Nspire: solve(16593.71 = k0*(1.0204)⁵,k0) ▸ k0=15000.

   Dvs. det oprindelige beløb var 15.000 kr.

2. Man skal løse ligningen 18749 = 16593,71·(1+r)⁵ med hensyn til r: solve(18749=16593.71*(1+r)⁵,r) ▸ r=0.024724

   Dvs. rentesatsen er 2,47 %

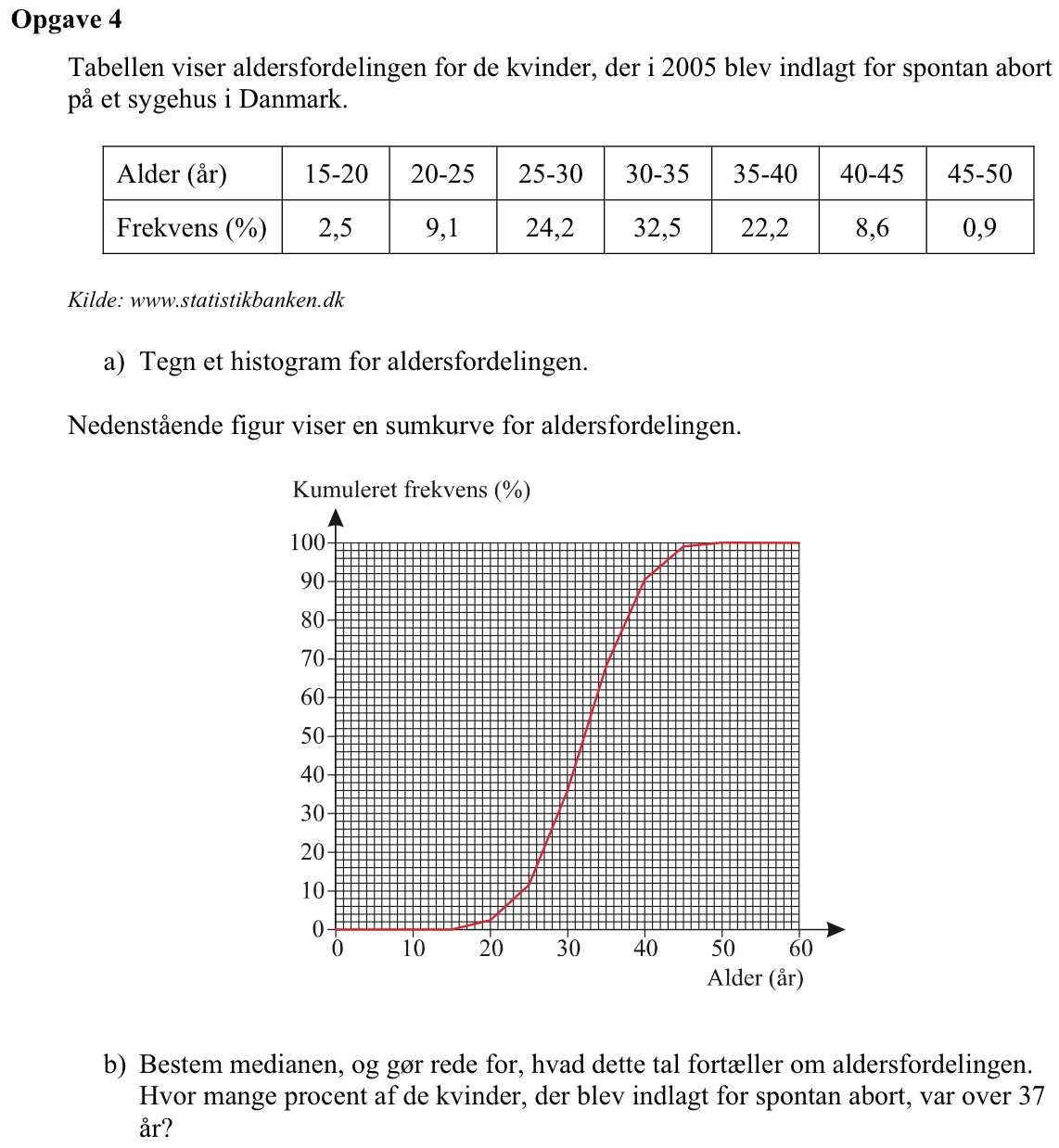
Svar på opgave 4:

1. Man opretter en liste i Ti-Nspire for den nedre værdi af aldersintervallerne:

   alder:={15,20,25,30,35,40,45} ▸ {15,20,25,30,35,40,45}

   Man opretter en liste med frekvenser for aldersintervallerne:

   frekvens:={2.5,9.1,24.2,32.5,22.2,8.6,0.9} ▸ {2.5,9.1,24.2,32.5,22.2,8.6,0.9}

   

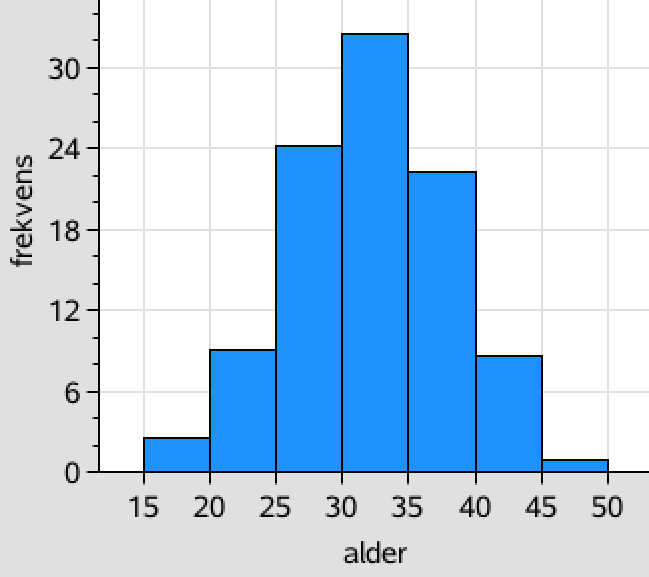
2. Medianen aflæses af sumkurven som vist.

   

   Medianen er 32 år, og det er den alder som halvdelen af kvinderne er under (eller over).

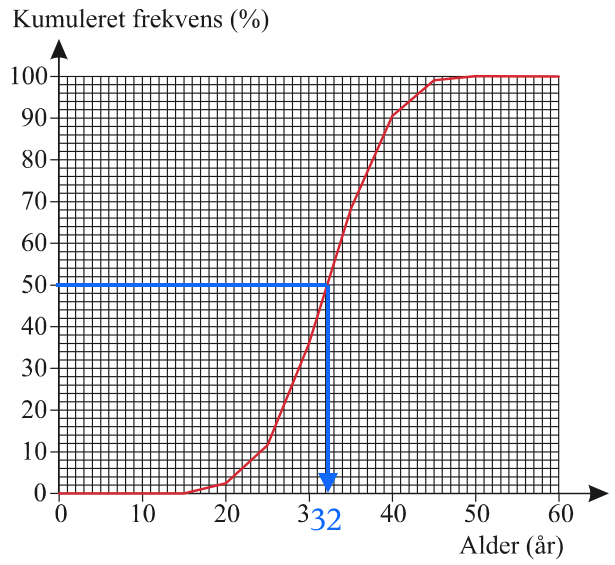
   Andelen af kvinder, der er over 37 år, findes ud fra sumkurven som vist nedenunder.

   

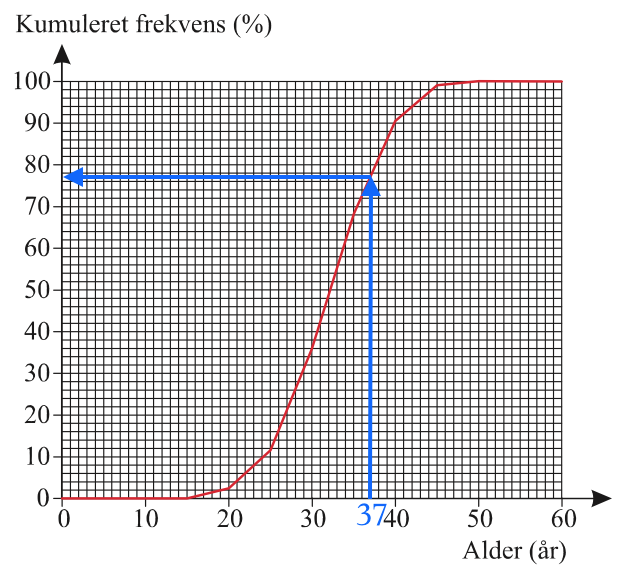
   Ud fra kurven aflæses andelen af kvinder, der er under 37 år til 77 %. Dvs. andelen af kvinder, der er over 37 år er 100 % - 77 % = 23 %

Svar på opgave 5:

1. Man indsætter x = (2009 - 1995) = 14 og får: 10,5·(1.044)¹⁴ mio. = 19,2 mio., som er antallet af indbyggere i Lagos i følge modellen i 2009.

   Fordoblingstiden findes af formlen: ln(2)/ln(a) = ln(2)/ln(1,044) år = 16,1 år

2. 10,5 mio. er indbyggertallet i 1995 (x=0), mens 1,044 er fremskrivningsfaktoren, dvs. det tal, man skal gange sidste års indbyggertal med for at få det nye.

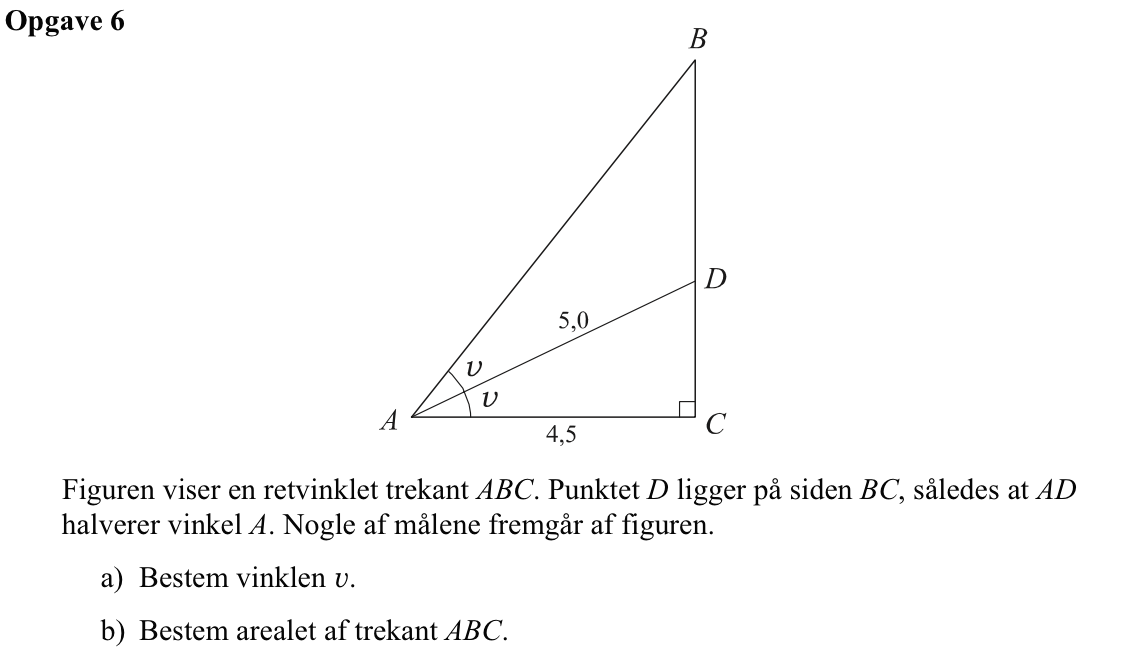
Svar på opgave 6:

1. Vinklen v findes ved hjælp af følgende trigonometriske formel for en retvinklet trekant: 5·cos(v) = 4,5 ⇒ cos(v) = 4,5/5 ⇒ v = cos^-1(4,5/5) ⇒ v = 25,8°

2. Arealet er 0,5·|AC|·|BC| = 0,5·4,5·|BC| = 0,5·4,5·4,5·tan(2·25,8°) = 12,8

Svar på opgave 7:

1. For at bestemme a og b skal man løse de sammenhængende lignnger: 19 = b·10^a og 11 = b·(25.)^a. Dette gøres i Ti-Nspire: solve(19=b*10^a and 11=b*(25.)^a,a,b) ▸ a=−0.596474 and b=75.0288

   Dvs a = −0,596 og b = 75,03

Svar på opgave 8:

1. Formlen er f(x) = 0,85x + 30, hvor f(x) er den månedlige udgift til mobiltelefon og x er antal minutter, som man taler om måneden.

2. For at finde antallet af minutter, som man skal tale i telefon, før det ene selskab er dyrere end det andet, skal man løse ligningen: 0,85·x + 30 = 0,99·x med hensyn til x. Dette gøres i Ti-Nspire: solve(0.85*x+30=0.99*x,x) ▸ x=214.3

   Dvs. man skal tale i 214,3 minutter pr. måned før det første telefonselskab er billigst.