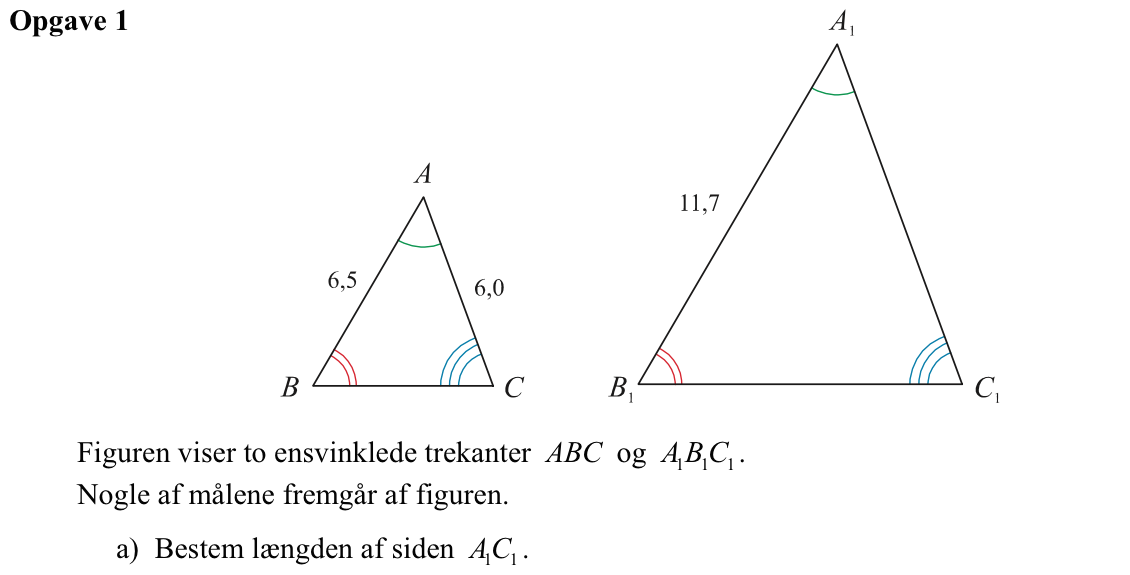
Svar på opgave 1:

1. For de to ensvinklede trekanter gælder: |A₁B₁|/|AB| = |A₁C₁|/|AC| ⇒ 10,7/6,5 = |A₁C₁|/6,0 ⇒ |A₁C₁| = 6,0·10,7/6,5 ⇒ |A₁C₁| = 9,88

Svar på opgave 2:

1. For at finde a og b skal man løse de sammenhørende ligninger: (1998-1998)·a + b = 13422 ∧ (2006-1998)·a + b = 19577 eller: b = 13422 ∧ 8·a + b = 19577 med hensyn til a og b. Dette gøre i Ti-Nspire

   solve((1998-1998)*a+b=13422 and (2006-1998)*a+b=19577.,a,b) ▸ a=769.375 and b=13422.

   Dvs. a = 769,4 og b = 13422

2. Konstanten a er den årlige vækst b er antallet af anmeldte voldsforbrydelser i 1998

3. For at finde det år, hvor antallet af anmeldte voldsforbrydelser overstiger 25000, skal man løse ligningen 769,4·x + 13422 = 25000.

   solve(769.375*x+13422=25000,x) ▸ x=15.0486

   Dette rundes af til 15 år, og man får årstallet 1998 + 15 = 2013 som det år, hvor antallet af anmeldte voldsforbrydelser overstiger 25000 i følge modellen.

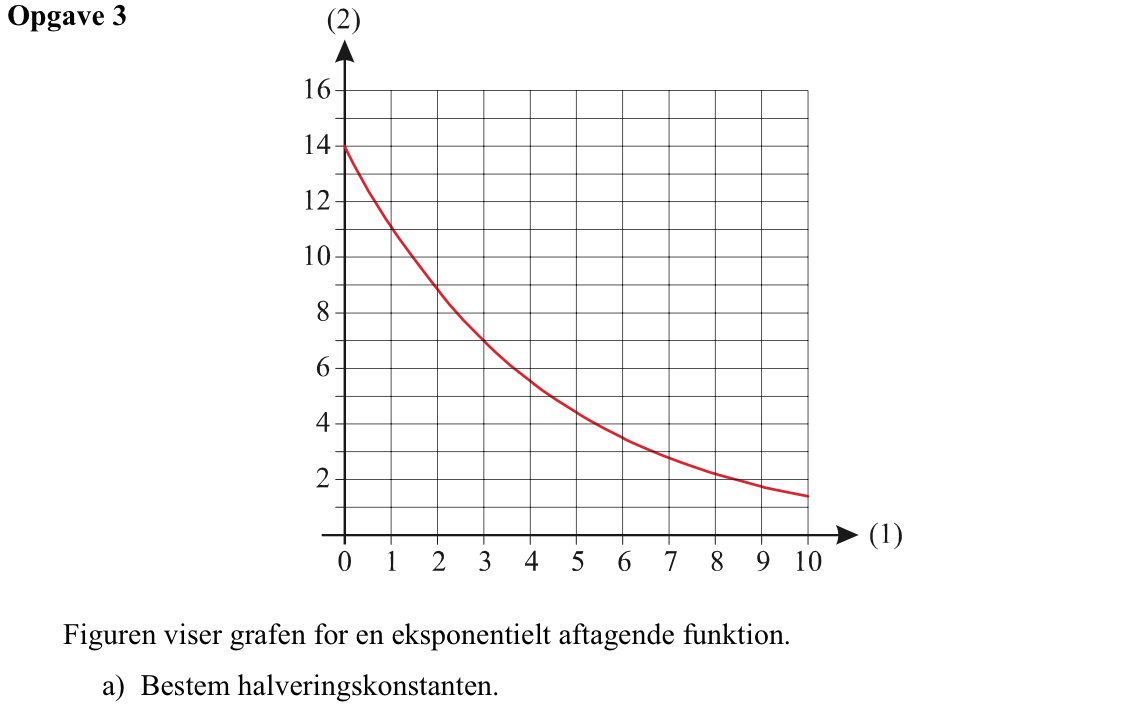
Svar på opgave 3:

1. Halveringskonstanten findes ud fra grafen som vist nedenunder:

   

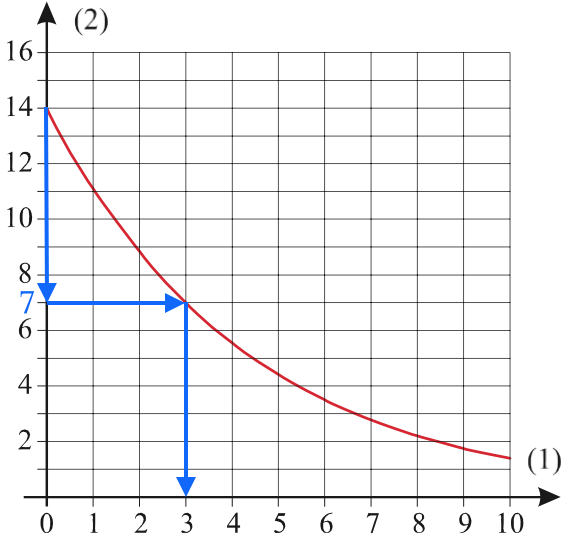
   Man starter med et punkt på kurven (her (x,y) = (0,14)) og halverer y-værdien. Dermed kommer man til punktet (0,7). Fra dette punkt gå man vandret hen til grafen og aflæser x-værdien til 3.

   Da dette er 3 højere end den x-værdi, som man startede med, er halveringskonstanten 3

Svar på opgave 4:

1. Man benytter, at trekant ABH er retvinklet og får derfor, at |AB|·sin(∠A) = |BH| ⇒ |BH| = 38·sin(67°) = 35,0

2. Areal = en halv grundlinje gange højde = 0,5·[2·38·cos(67°)]·[38·sin(67°)] = 519,4

Svar på opgave 5:

1. Modellen er f(x) = 5389·1,124^x, hvor f(x) er medlemstallet og x er antal år efter 1988.

2. Medlemstallet i 2006 er i følge modellen: 5389·(1,124)^(2006-1988) = 44.188

   Dette passer ikke med virkeligheden.

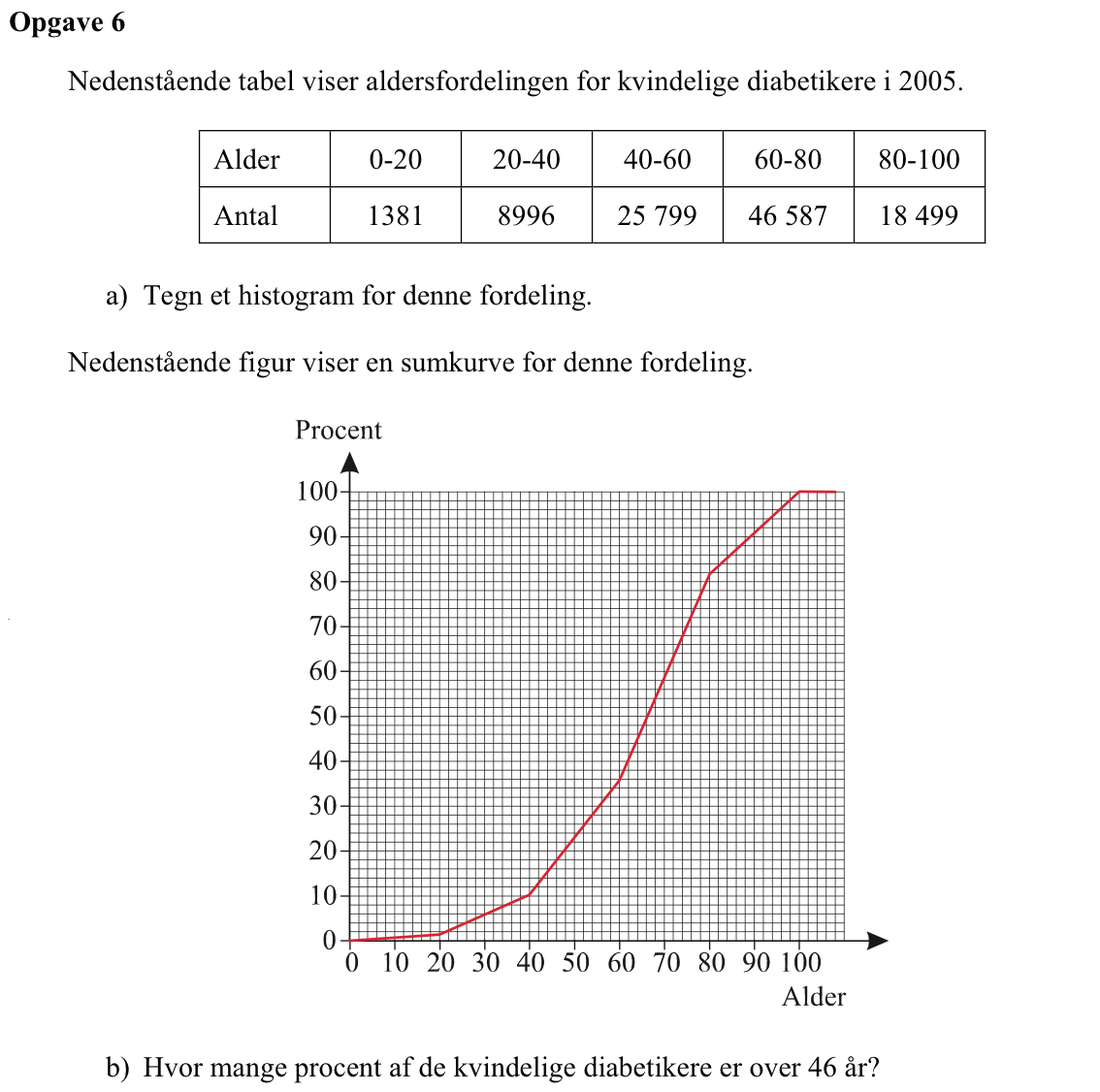
Svar på opgave 6:

1. Man opretter følgende lister i Ti-Nspire:

   alder:={0,20,40,60,80} ▸ {0,20,40,60,80}

   antal:={1381,8996,25799,46587,18499} ▸ {1381,8996,25799,46587,18499}

   Ud fra listerne tegnes et histogram:

   

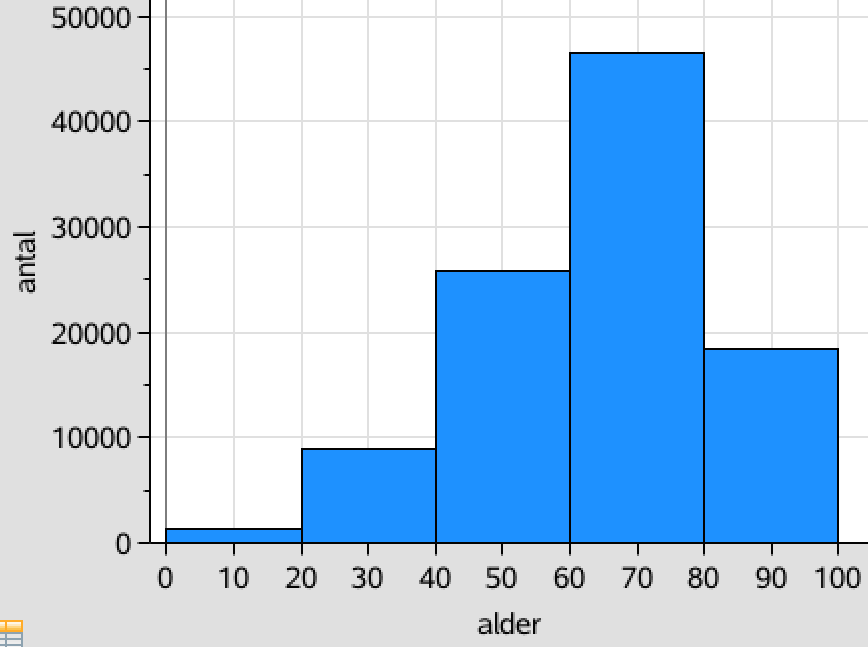
2. Ud fra sumkurven finder man andelen af kvindelige diabetikere, der er under 46 år:

   

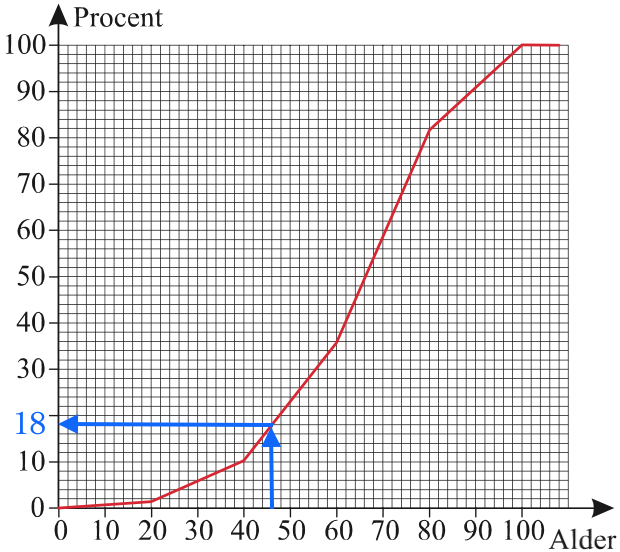
   Denne andel aflæses til 18%. Andelen som er over 46 år bliver derfor: 100 % - 18 % = 82 %

Svar på opgave 7:

1. Hestens vægt er 180²·160/11880 kg. = 436,4 kg.

   Gjordmålet bestemmes af ligningen 350 = gjordmål²·150/11880, der løses i Ti-Nspire: solve(350=gjordmål²*150/11880.,gjordmål)|gjordmål>0 ▸ gjordmål=166.493

   Dvs. gjordmålet på hesten er 166 cm

Svar på opgave 8:

1. Diamantens vægt i karat er 0,0033·(27,6)^3,06 = 84,7 karat

2. Ved at bruge procent-procentvækst reglen for potensfunktioner får man, at den store diamants vægt er (1,2^3,06 - 1)·100 % = 74,7 % større end den lilles.