Svar på opgave 1:

1. Man skal bruge kapitalformlen: K = K₀·(1 + r)ⁿ. Her skal man finde K. K₀ = 8700, r = 4 % (= 0,04) og n = 7. Dette gver:

   K = 8700·(1 + 4 %)⁷ = 8700·1,04⁷ = 11.448,60.

   Dvs. det indestående beløb efter 7 år er 11.449 kr.

Svar på opgave 2:

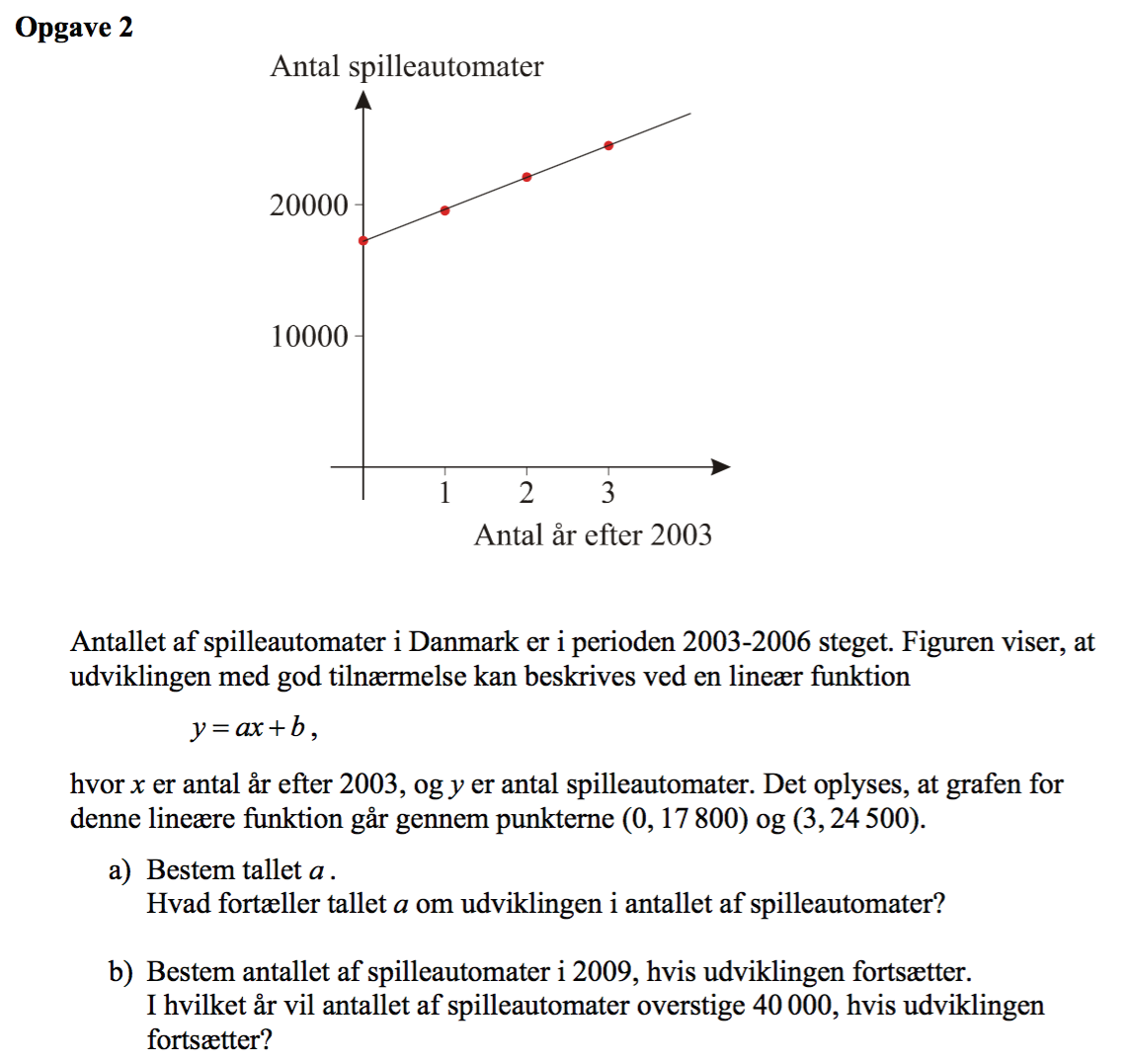
1. Tallet a er hældningen til den rette linje. Den findes som forskellen i y-værdier for de to punkter divideret med forskellen i x-værdier.

   Man får a = (24500 - 17800)/(3 - 0) = 2.233,33 = 2.233 (Man kan tilføje enheden: spilleautomater pr. år).

   Tallet a er den årlige stigning i antallet af spilleautomater i Danmark.

2. Man skal finde tallet b i formlen y = a·x + b. Man sætter x = 0 og får y = b. Dvs. b er y-værdien til punktet (0,17800), som er 17800.

   Den færdige formel er derfor: y = 2233·x + 17800. Man nu finde værdien for året 2009. Da x = 0 svarer til 2003, vil det sige at 2009 svarer til x = 2009 - 2003 = 6. Indsættes x = 6 får man:

   y = 2333·6 + 17800 = 31.798

   Dvs. i 2009 er der i følge modellen 31.798 spilleautomater i Danmark.

   Man skal løse ligningen 40.000 = 2333·x + 17800 med hensyn til x for at finde antallet af år efter 2003. Dette giver:

   40.000 = 2.333·x + 17.800 ⇔

   (40.000 - 17.800) = 2.333·x ⇔

   (40.000 - 17.800)/2.333 = x ⇔

   x = 9,5

   9,5 år efter 2003 er 2013, idet man vælger at runde op, så man får det første år, hvor antallet af spilleautomater er over 40000 hele året.

   Dvs. det år hvor antallet af spilleautomater overstiger 40.000 er 2013

Svar på opgave 3:

1. Som vist på nedenstående tegning gælder at 16,2·sin(∠A) = 9,5.

   

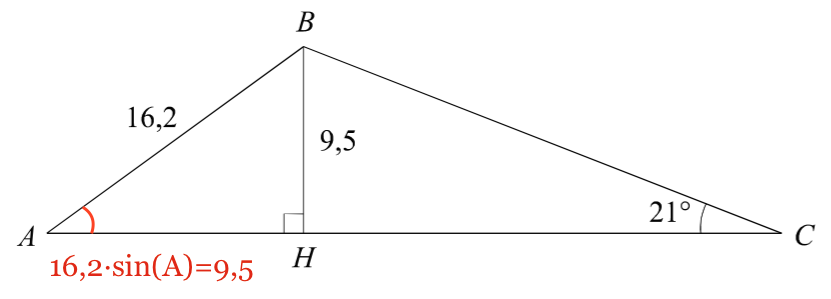
   Heraf følger: 16,2·sin(∠A) = 9,5 ⇔

   sin(∠A) = 9,5/16,2 ⇔ (idet man ved, at vinklen ligger mellem 0 og 90°)

   ∠A = sin^-1(9,5/16,2) ⇔

   ∠A = 35,9°

2. Som vist på tegningen nedenunder gælder: |AH| = 16,2·cos(∠A) og tan(21°) = 9,5/|HC| ⇔ |HC| = 9,5/tan(21°).

   

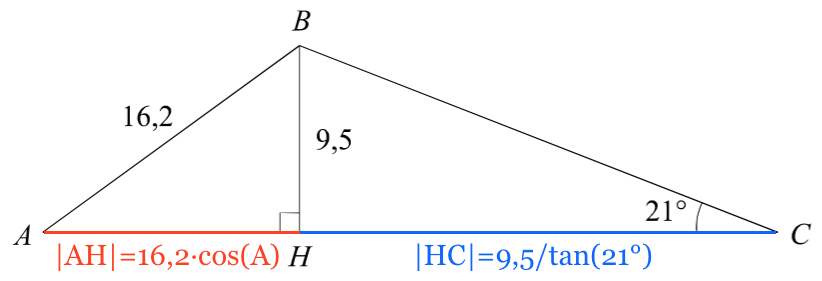
   |AC| = |AH| + |HC| = 16,2·cos(35,9°) + 9,5/tan(21°) = 37,871 = 37,9

Svar på opgave 4:

1. Man inddfører x og y i tabellen som vist:

   

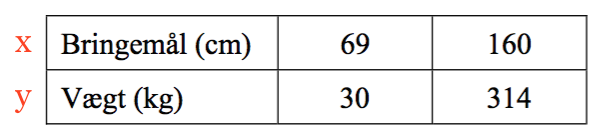
   Man løse de to sammenhørende ligninger: 30 = b·69^a og 314 = b·160^a med hensyn til a og b. Man får følgende i Ti-Nspire:

   solve(30.=b*69^a and 314=b*160^a,a,b) ▸ a=2.79192 and b=0.00022

   Dvs. a = 2,792 og b = 0,00022

   Det kan også løses i hånden: 30 = b·69^a ∧ 314 = b·160^a ⇔

   b = 30/69^a ∧ 314 = (30/69^a)·160^a ⇔

   b = 30/69^a ∧ 314/30 = (160/69)^a ⇔

   b = 30/69^a ∧ ln(314/30) = ln((160/69)^a) ⇔

   b = 30/69^a ∧ ln(314/30) = a·ln(160/69) ⇔

   b = 30/69^a ∧ a = [ln(314/30)]/ln(160/69) ⇔

   b = 30/69^2,79192 ∧ a = 2,79192 ⇔

   a = 2,79192 ∧ b = 0,00022

2. Man skal finde y, når x = 130. Man får: y = 0,00022·130^2,792 = 175,61.

   Dvs. vægten af en kvie med et bringemål på 130 cm er 176 kg.

3. Man bruger formlen for procent-procent vækst for en potensfunktion. Fremskrivningsfaktoren er 1 + 10 % = 1,10.

   Den procentvise stigning i vægt er derfor: (1,10^2,792 - 1)·100 % = 30,5 %

Svar på opgave 5:

1. Det midterste ord på den sorterede liste er medianen. Dette er tal nummer 13 ud af de 25, som er tallet 4. Dermed er medianen 4

   Middeltallet er summen af tallene på listen divideret med antallet af tal på listen, som er 25. Man får middeltallet: (2+2+2+2+2+3+3+3+3+3+4+4+4+4+4+5+5+6+6+6+7+7+7+7+14)/25 = 4,6

2. Man skal finde kvartilsættet, hvor man kender medianen. Man tager nu medianen ud af listen og betragter de to lister med de tolv tal, der kommer før medianen og de tolv tal, der kommer efter. På disse to lister skal man finde nedre og øvre kvartil.

   Den første liste har to tal i midten (tallen på pladserne seks og syv). Disse to tal er begge 3. Disse to tal tager man gennemsnittet af og får 3. Dermed er nedre kvartil 3.

   Den anden liste (med tal, der er større end medianen) har to tal i midten (tallen på pladserne 19 og 20). Disse to tal er begge 6. Disse to tal tager man gennemsnittet af og får 6. Dermed er øvre kvartil 6.

   På listen nedenunder er inddelingerne vist:

   

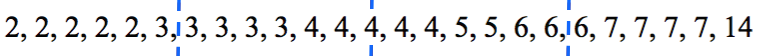
   Dertil tilføjer man listens største og mindste værdier: 2 og 14. Dette giver det blå boks-plot, som er vist sammen med boks-plottet for HF-bekendtgørelsen på figuren nedenunder:

   

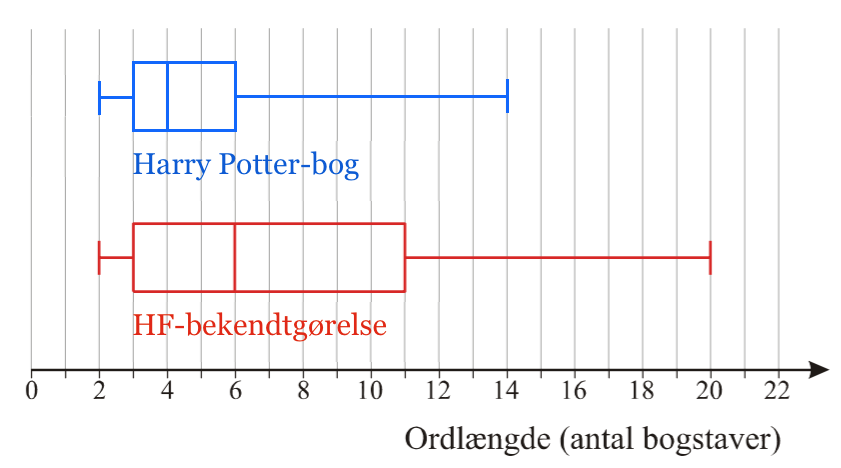
   Af medianerne, de øvre kvartiler og de højeste værdier på boks-plottene ses, at ordene i Harry Potter-bogen generelt er kortere end i HF-bekendtgørelsen.

Svar på opgave 6:

1. Tallet 14 er startværdien dvs. antallet af indbyggere målt i millioner i år 2000. Det indses ved at indsætte x = 0 i formlen.

   Tallet 1,023 er fremskrivningsfaktoren, dvs. det tal, som man skal gange forrige års indbyggerantal med for at få det nye års antal. Man kan også af tallet finde den årlige vækstrate i indbyggertallet, som er (1,023 - 1)·100 % = 2,3 %.

Svar på opgave 7:

1. Man har formlen m = k·d²·h, hvor m = 7,0; d = 23,35 og h = 2,30. Dette giver:

   7,0 = k·23,35²·2,30 ⇔ k = 7,0/(23,35²·2,30) = 0,00558

   Dvs. k = 0,00558 g/mm³ = 5,58 g/cm³ for den danske 10-krone.

Svar på opgave 8:

Nedenstående skema viser, at forholdet mellem forbrug og indekstal er ens for hvert år. De ubekendte kaldes som vist x og y.

1. Forbruget i 2003 kaldes x. Der gælder at: 7,3/100 = x/114 ⇔ 114·7,3/100 = x ⇔ x = 8,322.

   Dvs. forbruget af vin og spiritus var 8,3 mia. kr. i 2003

   Indekstallet for 2006 kaldes y. Der gælder at: 7,3/100 = 9,4/y ⇔ y = 9,4/(7,3/100) = 100·9,4/7,3 = 128,8.

   Dvs. indekstallet for forbruget af vin og spiritus var 129 i 2006

2. Man skal forestille sig at forbruget hvert år vokser med en bestemt procentsats ligesom penge på en opsparing.

   Af indekstallet for 2009 ses, at forbruget af vin og spiritus er vokset fra indeks 100 til indeks 129 på 9 år (2009 - 2000).

   Den gennemsnitlige årlige vækst kaldes x. Man har:

   100·(1 + x)⁹ = 129 ⇔

   (1 + x) = ⁹√[1,29] ⇔

   x = ⁹√[1,29] - 1 ⇔

   x = 0,0287

   Dvs. den gennemsnitlige årlige vækst er 2,87 %