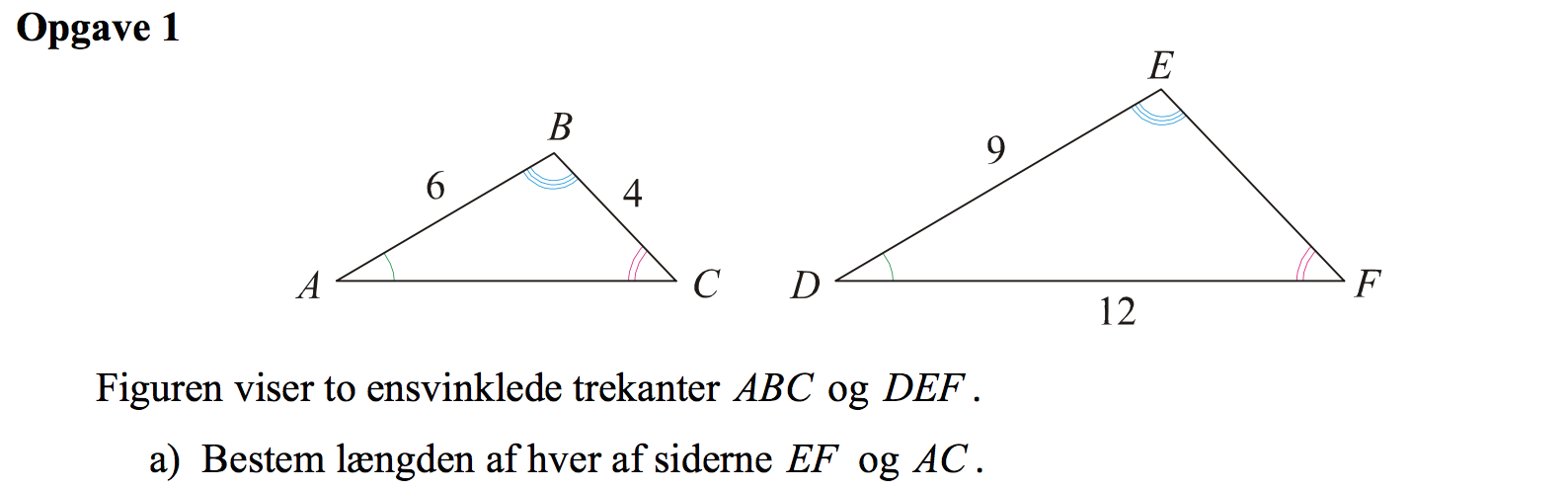
Svar på opgave 1:

1. De to trekanter ΔABC og ΔDEF er ensvinklede, og der gælder dermed samme forhold for ensliggende sider i de to trekanter (skaleringsfaktoren). Figuren herunder viser hvilke sider i de to trekanter, der er ensliggende:

   

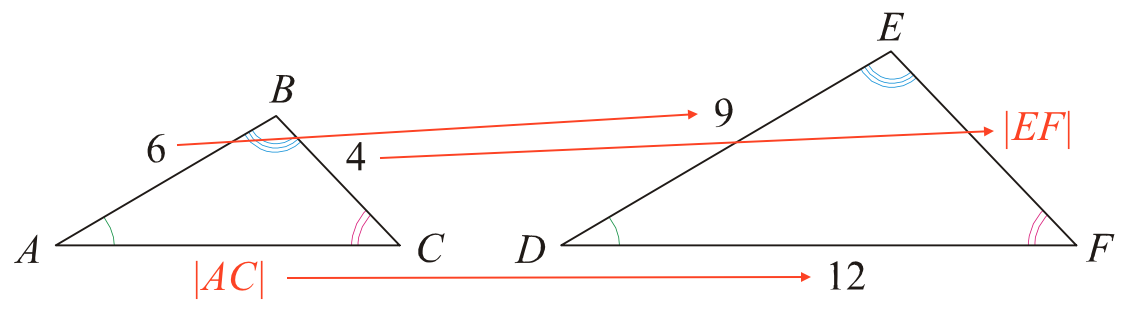
   Dvs. 6/9 = 4/|EF| = |AC|/12. Af dette får man:

   4/|EF| = 6/9 ⇔ |EF|/4 = 9/6 ⇔ |EF| = 4·9/6 = 6

   |AC|/12 = 6/9 ⇔ |AC| = 12·6/9 = 8

Svar på opgave 2:

1. Tallet 2,5 er den årlige vækst i antal mia. kr. i spil. Tallet 10,5 er omsætningen på spil i år 2000 (= startværdien. Dette indses ved at sætte x = 0.)

2. År 2005 svarer til x = 5. Indsættes denne værdi af x i formlen for man omsætningen: (2,5·5 + 10,5) mia. kr. = 23 mia. kr.

   Dette passer nogenlunde med det rigtige tal, dog lidt i underkanten.

Svar på opgave 3:

1. Man skal bruge kapitalformlen K = K₀·(1 + r)ⁿ, hvor K = 8877,62 kr., K₀ = 8000 kr., n = 6. Man skal finde r og får:

   8877,62 = 8000·(1 + r)⁶ ⇔

   8877,62/8000 = (1 + r)⁶ ⇔

   ⁶√[8877,62/8000] = ⁶√[(1 + r)⁶] ⇔

   ⁶√[8877,62/8000] = 1 + r ⇔

   r = ⁶√[8877,62/8000] - 1 ⇔

   r = 0,0175 = 1,75 %

   Dvs. rentesatsen er 1,75 %

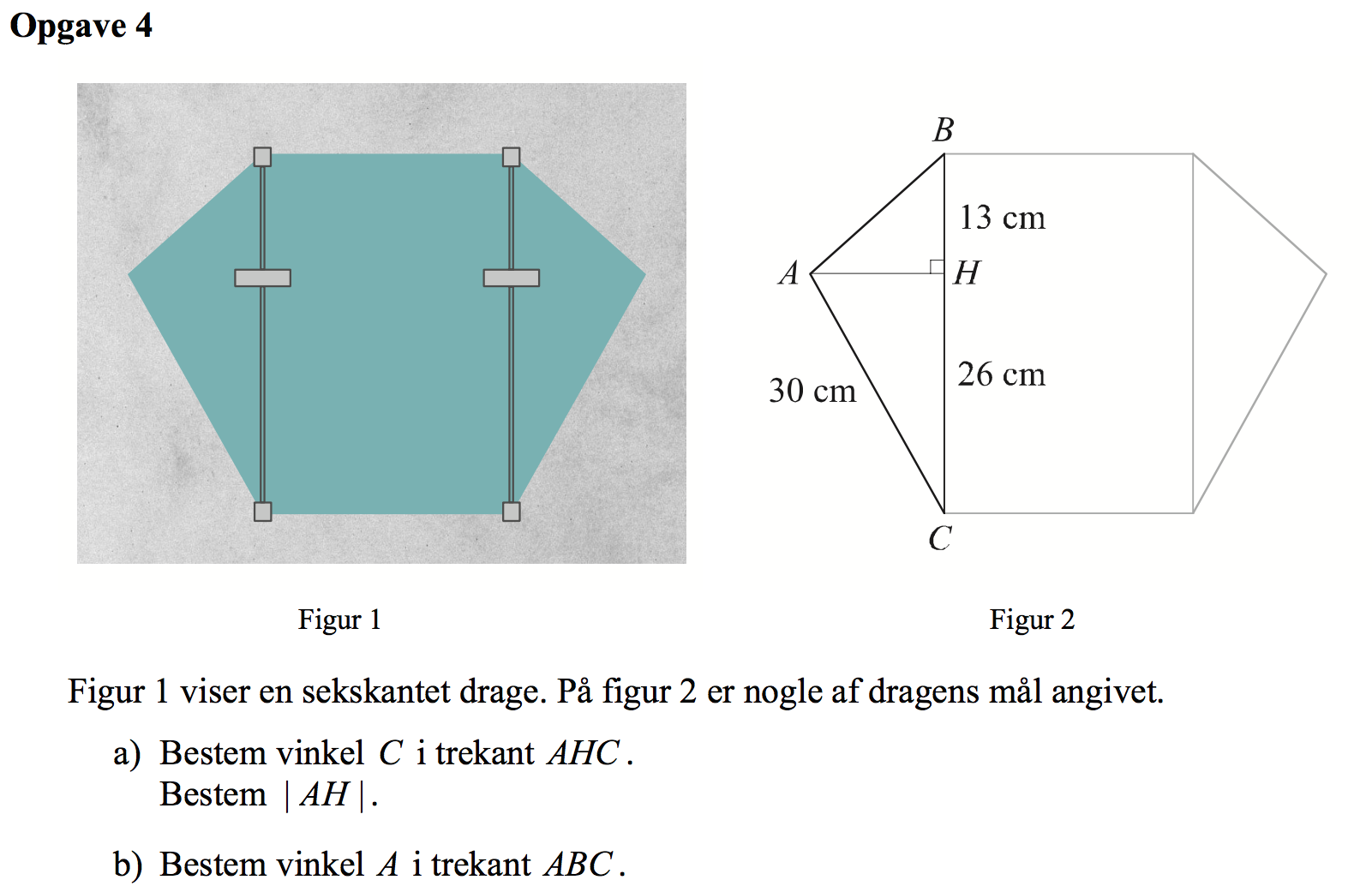
Svar på opgave 4:

1. ΔAHC danner en retvinklet trekant, hvor AC er hypotenusen. Der gælder:

   |AC|·cos(∠C) = |AH| ⇒

   30·cos(∠C) = 26 ⇔

   cos(∠C) = 26/30 ⇒

   ∠C = cos^-1(26/30) ⇔

   ∠C = 29,9°

   Den trigonometriske sammenhæng er vist på figuren nendenunder:

   

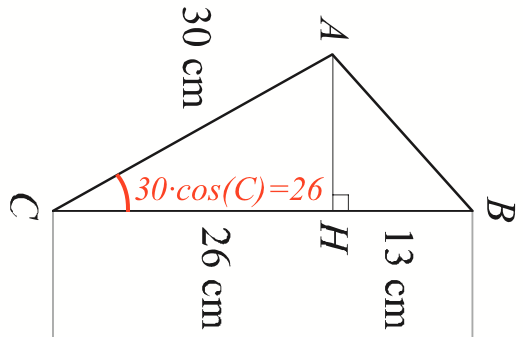
   AH er katete i den retvinklede trekant ΔAHC. Dermed kan |AH| findes ved hjælp af Pythagoras læresætning:

   |AH|² = 30² - 26² ⇔

   |AH| = √[30² - 26²] = 14,97

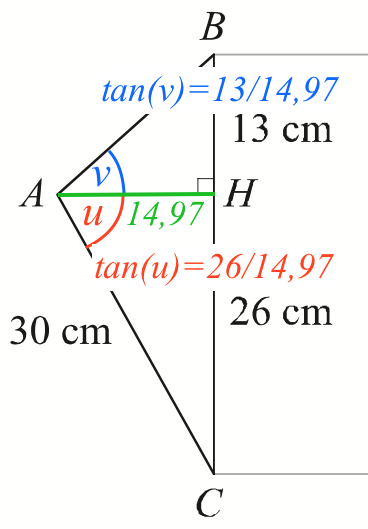
2. Man deler vinkel A op i to vinkler: v og u. Som vist nedenfor er tan(v) = |BH|/|AH| ⇒

   tan(v) = 13/14,97 = 0,8684 ⇒

   v = tan^-1(0,8684) ⇔

   v = 40,97°

   Tilsvarende er u = tan^-1(26/14,97) = 60,07°

   ∠A = v + u = 40,97° + 60,07° = 101,0°

   

Svar på opgave 5:

1. Der er tale om en procentuel årlig vækst og ikke en væskt med et fast antal eller mængde der lægges til for hvert år. Derfor er modellen en eksponential vækst på formen:

   y(x) = b·a^x, hvor y er antallet af internetbutikker et bestemt år og x er antal år efter 2006. Tallet a er fremskrivningsfaktoren, som her er 1 + 40% = 1,40. Tallet b er startværdien dvs. antallet af internetbutikker i 2006 som var 7700 (dette indses ved at sætte x = 0 i formlen, der derved giver y(0) = b).

   Dvs. man får modellen: y(x) = 7700·1,4^x

2. Man skal først løse ligningen y(x) = 25000 med hensyn til x. Dette giver:

   25000 = 7700·1,4^x ⇔

   25000/7700 = 1,4^x ⇔

   ln(25000/7700) = ln(1,4^x) ⇔

   ln(25000/7700) = x·ln(1,4) ⇔

   x = ln(25000/7700)/ln(1,4) ⇔

   x = 3,50

   Dvs. antallet af internetbutikker passerer 25000 efter 3,5 år eller i løbet af år 2009. Det første år, hvor man er over 25.000 internetbutikker fra starten af året er således 2010

   (Hvis man er i tvivl, så udregn: y(3) = 21128,8 og y(4) = 29580,3. Det ses, at 25000 ikke er passeret efter 3 år, og at man derfor skal runde op.)

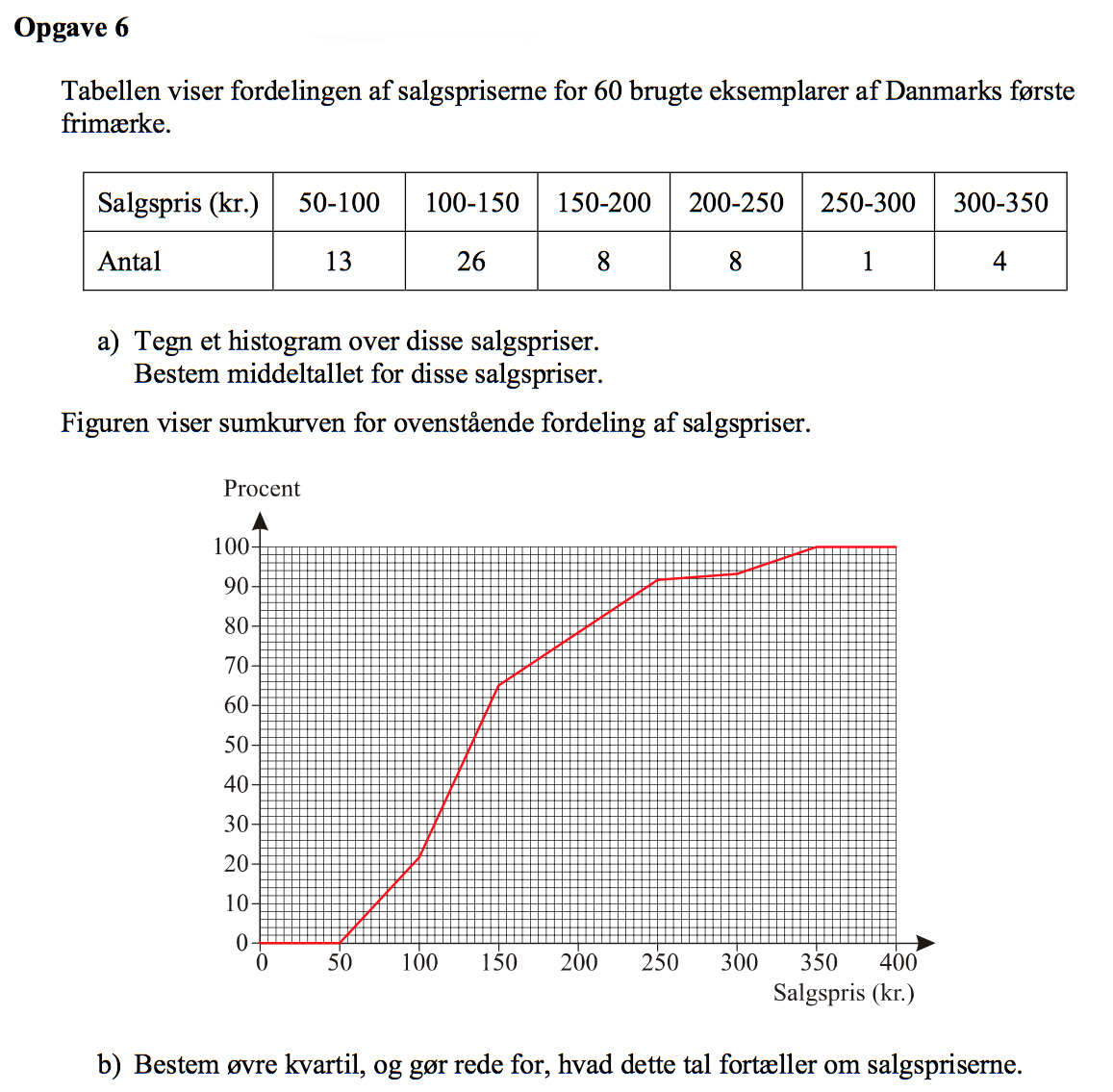
Svar på opgave 6:

1. Nedenstående histogram er lavet i Ti-Nspire med følgende lister:

   salgspris:={50,100,150,200,250,300} = {50,100,150,200,250,300}

   antal:={13,26,8,8,1,4} = {13,26,8,8,1,4}

   

   Middeltallet for salgspriserne er middeltallet for det enkelte interval gange frekvensen for intervallet. Frekvensen for et interval er igen antallet i intervallet (også kaldet hyppigheden for intervallet) divideret med summen af antal. Summen af antal er 13 + 26 + 8 + 8 +1 + 4 = 60.

   Middeltallet er derfor: (13/60)·(50 + 100)/2 + (26/60)·(100 + 150)/2 + (8/60)·(150 + 200)/2 + (8/60)·(200 + 250)/2 + (1/60)·(250 + 300)/2 + (4/60)·(300 + 350)/2 = 150

2. Øvre kvartil er er 75 %-fraktilen for fordelingen. Den aflæses ud fra sumkurven som vist nedenunder:

   

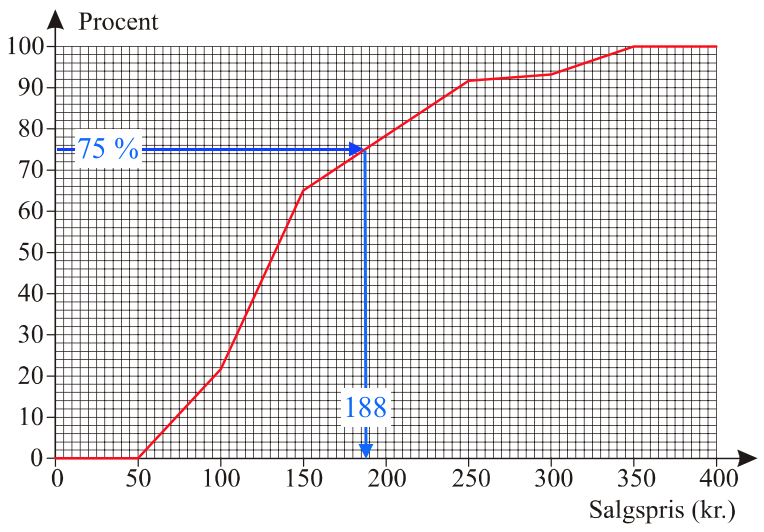
   Dvs. øvre kvartil er 188

   Dette tal er den salgspris, som 75 % af frimærkerne ligger under.

Svar på opgave 7:

1. Man har følgende (uden enheder):

   Menneske: x = 70, y = 5,9

   Hund: x = 20, y = 1,5

   Man skal løse de to sammenhørende ligninger: 5,9 = b·70^a ∧ 1,5 = b·20^a med hensyn til a og b. Man får:

   5,9 = b·70^a ∧ 1,5 = b·20^a ⇔

   b = 5,9/(70^a) ∧ 1,5 = [5,9/(70^a)]·20^a ⇔

   b = 5,9/(70^a) ∧ 1,5/5,9 = 20^a/70^a ⇔

   b = 5,9/(70^a) ∧ 0,254237 = (20/70)^a ⇔

   b = 5,9/(70^a) ∧ ln(0,254237) = ln(0,285714^a) ⇔

   b = 5,9/(70^a) ∧ ln(0,254237) = a·ln(0,285714) ⇔

   b = 5,9/(70^a) ∧ a = ln(0,254237)/ln(0,285714) ⇔

   b = 5,9/(70^1,09317) ∧ a = 1,09317 ⇔

   a = 1,09317 ∧ b = 0,056734

   Dvs. a = 1,093 og b = 0,0567

2. For elefanten er y = 787 kg. Man skal løse ligningen: 787 = 0,0567·x^1,093. Man får:

   787 = 0,0567·x^1,093 ⇔

   787/0,0567 = x^1,093 ⇔

   (787/0,0567)^(1/1,093) = (x^1,093)^(1/1,093) ⇔

   x = (787/0,0567)^1/1,093 ⇔

   x = 6164,93

   Dvs. elefantens kropsvægt er 6.164 kg

3. For at løse opgaven indfører man fire variable:

   x_b: bengalkattens kropsvægt

   x_s: siameserkattens kropsvægt

   y_b: bengalkattens skeletvægt

   y_s: siameserkattens skeletvægt

   Bengalkatten vejer 50 % mere end siameserkatten vil sige, at x_b er 50 % større end x_s eller

   x_b = 1,50·x_s.

   Den procentdel, som bengalkattens skeletvægt er større end siameserkattens skeletvægt, findes ved formlen:

   [(y_b - y_s)/y_s]·100 % =

   [(0,0567·(x_b)^1,093 - 0,0567·(x_s)^1,093)/(0,0567·(x_s)^1,093)]·100 % =

   [(0,0567·(1,5·x_s)^1,093 - 0,0567·(x_s)^1,093)/(0,0567·(x_s)^1,093)]·100 % =

   (1,5^1,093 - 1)·100 % = 55,8 %

   Dvs. bengalkattens skeletvægt er 56 % større end siameserkattens.

Svar på opgave 8:

1. Kald rørets længde x og grundtonens frekvens y. Når x og y er ligefrem proportionale gælder: y = k·x, hvor k er en konstant.

   Tilsvarende gælder ved omvendt proportionalitet at y = k/x.

   Man finder k af oplysningerne y = 880 og x = 9,4 ⇒ k = 880·9,4 = 8272

   Når grundtonen er 588 Hz, er y = 588. Dette giver: 588 = 8272/x ⇒ x = 8272/588 = 14,068

   Dvs. rørets længde er 14,1 cm

   En anden måde at løse det på er: Ved omvendt proportionalitet gælder følgende: x₁·y₁ = x₂·y₂ ⇒

   9,4·880 = x₂·588 ⇔

   x₂ = 9,4·880/588 ⇔

   x₂ = 14,068