Svar på opgave 1:

1. Man skal bruge kapitalformlen: K = K₀·(1 + r)ⁿ, hvor K₀ = 15.000 kr., r = 2,4 % = 0,024 og n = 10. Man skal finde K:

   K = (15.000 kr.)·(1 + 2,4%)¹⁰ = 15.000·1,024¹⁰ kr. = 19014,80 kr.

   Dvs. der står 19.014 kr. på kontoen efter 10 år.

Svar på opgave 2:

1. Man har punkterne (x,y) = (-6,2) og (x,y) = (2,8). For at disse punkter skal ligge på linjen med ligningen y = ax + b, skal der gælde:

   2 = a·(-6) + b ∧ 8 = a·2 + b ⇔

   b = 2 + 6a ∧ 8 = a·2 + 2 + 6a ⇔

   b = 2 + 6a ∧ 6 = 8a ⇔

   b = 2 + 6·(0,75) ∧ 0,75 = a ⇔

   b = 6,5 ∧ 0,75 = a ⇔

   Dvs. a = 0,75 og b = 6,5

Svar på opgave 3:

1. Man opretter lister med boligstørrelse og frekvens. Listen med boligstørrelser indeholder som første element nedre grænse for første interval og derefter øvre grænse for hvert interval. Man vedtager at øvre grænse for boligstørrelse er 140 m².

   Ud fra frekvenserne finder man de kummulerede frekvenser. Dette er gjort nedenunder i Ti-Nspire. Listen med kummulerede frekvenser kaldes kum_frekvens.

   boligstørrelse:={0,40,60,80,100,120,140} ▸ {0,40,60,80,100,120,140}

   frekvens:={0,5,21,35,25,8,6} ▸ {0,5,21,35,25,8,6}

   kum_frekvens:=cumulativeSum(frekvens) ▸ {0,5,26,61,86,94,100}

   Ud fra listerne boligstørrelse og kum_frekvens tegnes nedenstående sumkurve:

   

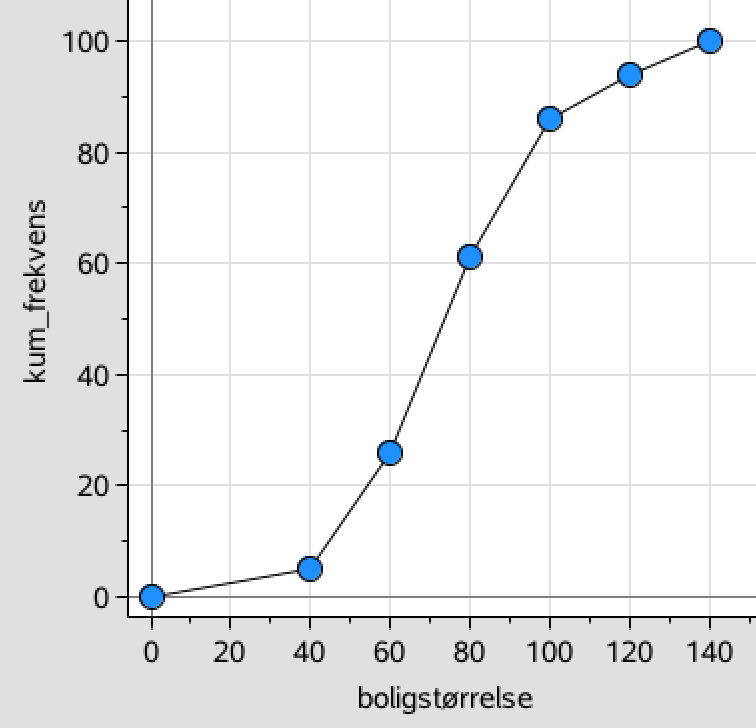
2. Medianen bestemems ud fra sumkurven ved at finde den boligstørrelse der svarer til 50% på kurven. Dette er vist nedenunder.

   

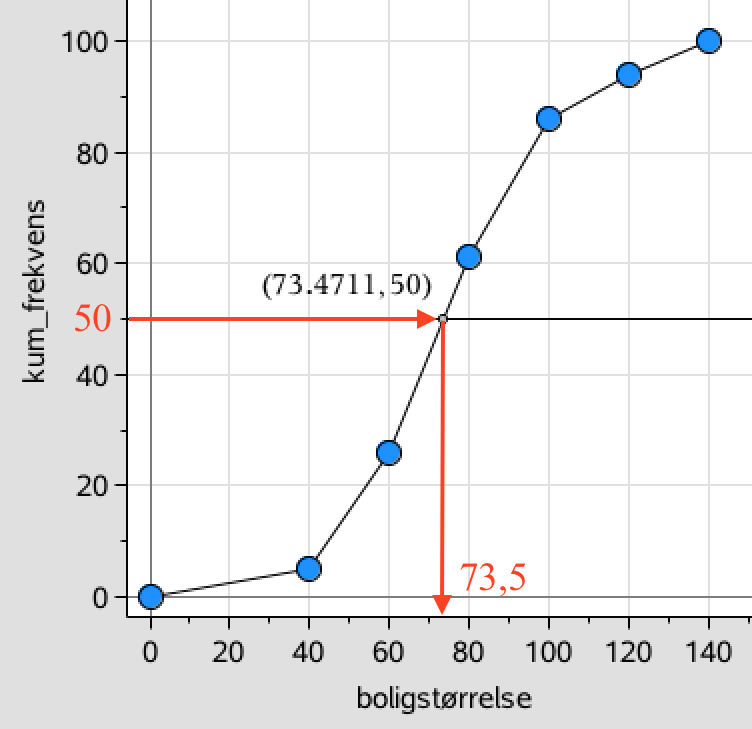
   Medianen aflæses på førsteaksen til 73,5 m²

   Dette tal viser hvilken størrelse, som halvdelen af boligerne ligger under.

3. Man skal først finde den procentdel på sumkurven, der svarer til 95 m². Dette er vist nedenunder:

   

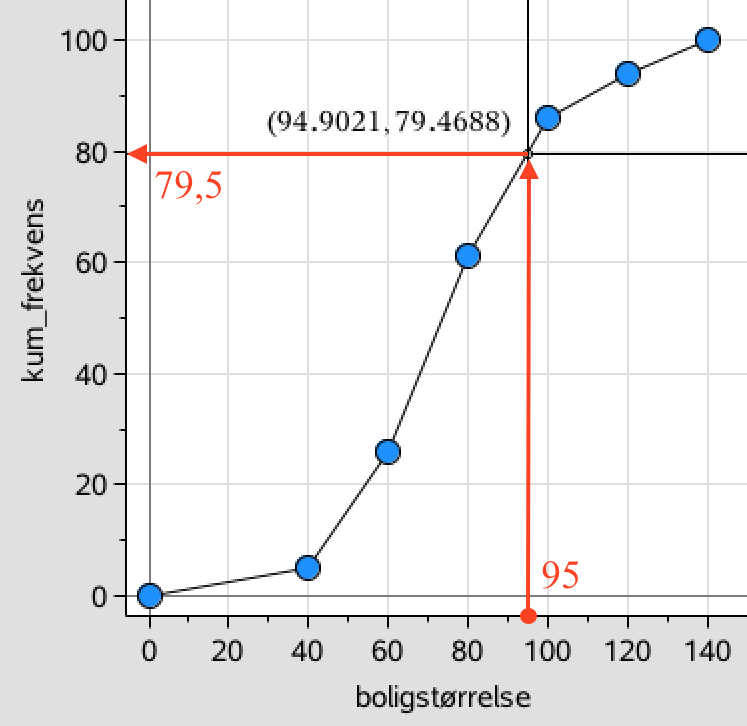
   Procentdelen aflæses til 79,5 %. Dette er den procentdel af boligerne, der er under 95 m².

   Andelen, som er over 95 m², bliver derfor 100 % - 79,5 % = 20,5 %

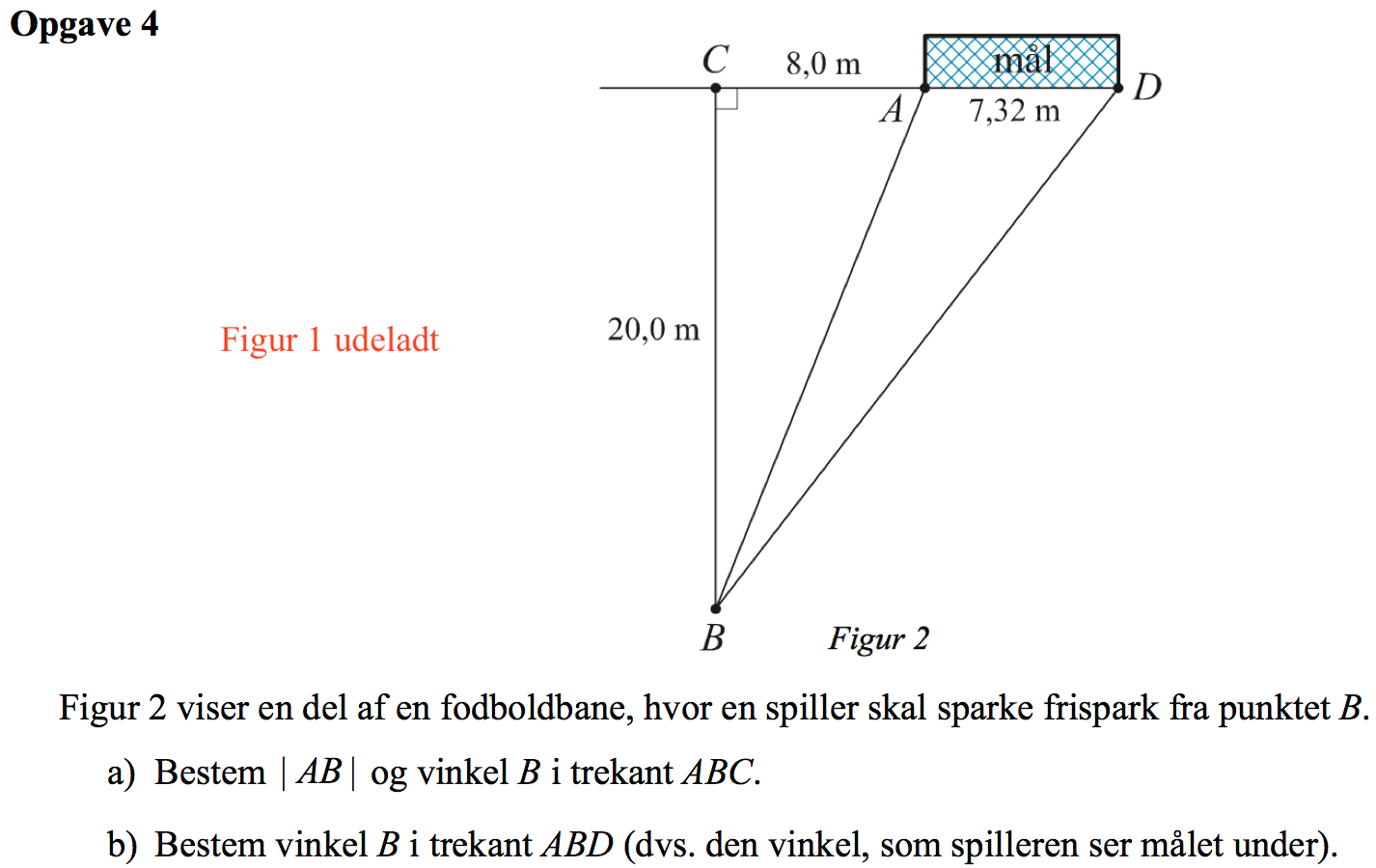
Svar på opgave 4:

1. Trekant ABC er retvinklet. Dvs. at man kan bruge Pythagoras læresætning til at finde |AB|, som er hypotenusen i trekant ABC. Der gælder at: |AB|² = |BC|² + |CA|² ⇒

   |AB|² = 20,0² + 8,0² ⇔

   |AB|² = 400,0 + 64,0² ⇔

   |AB|² = 464,0 ⇔

   |AB| = √[464,0] ⇔

   |AB| = 21,54

   Dvs. længden af siden AB er 21,5 m

   Vinkel B i trekant ABC kaldes v. Der gælder at tan(v) = 8,0/20,0 ⇒

   tan(v) = 0,40 ⇒

   v = tan^-1(0,40) ⇒

   v = 21,8°

   Vinkel B i trekant ABC er 21,8°

   Brugen af Pythagoras læresætning og reglen om tangens for en vinkel i en retvinklet trekant er vist på figuren nedenunder:

   

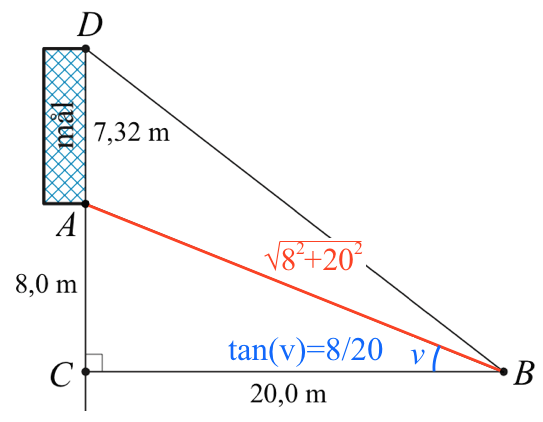
2. Man kalder vinkel DBC for u. Man skal finde vinkel DBA, som er lig med u - v = u - 21,8°.

   Vinken u findes som før ved hjælp af reglen om tangens til en vinkel i en retvinklet trekant:

   tan(u) = (8,0+7,32)/20,0 = 15,32/20,0 = 0,766

   u = tan^-1(0,766) = 37,45°

   Dette giver at vinklen B i trekant DBA = 37,45° - 21,8° = 15,7°

   Beregningen af vinkel u (eller ∠ DBC) er vist nedenunder:

   

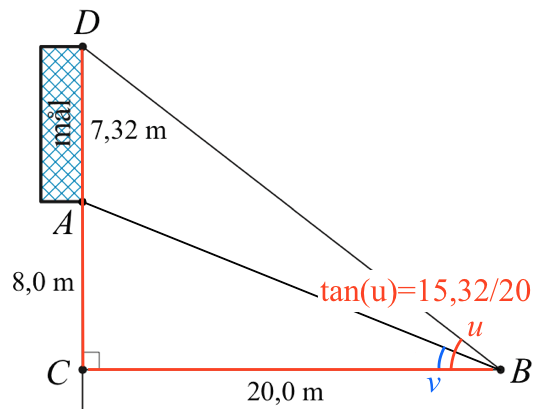
Svar på opgave 5:

1. Modellen er en eksponentiel model, y = b·a^x, hvor y er antallet af tilfælde af modermærkekræft og x er antal år efter 2003.

   Tallet a er fremskrivningsfaktoren dvs. det tal som sidste års antal skal ganges med for at få dette års antal. Der gælder også at a = 1 + vækstraten, hvor vækstraten er 5,5 % = 0,055. Dette giver at a = 1,055.

   Tallet b er startværdien, dvs. antallet modermærkekræfttilfælde i 2003, som er 1222.

   Modellen er y = 1222·1,055^x

2. Man skal finde det år, hvor y = 2100. Først finder man det x, som giver denne y-værdi.

   2100 = 1222·1,055^x ⇔

   2100/1222 = 1,055^x ⇔

   ln(2100/1222) = ln(1,055^x) ⇔

   ln(2100/1222) = x·ln(1,055) ⇔

   x = ln(2100/1222)/ln(1,055) = 10,113

   Denne x-værdi svarer til et tidspunkt i 2003 + 10 = 2013. Hvis der menes det første år hvor antal modermærkekræft tilfælde er større end eller lig med 2100 er svaret 2014.

   Dvs. 2100 årlige tilfælde af modermærkekræft overstiges i 2014

Svar på opgave 6:

1. Luftmodstanden er 0,035·80² Newton = 224 N, når bilen kører 80 km/t.

2. Man skal bruge formlen for procent-procent vækst for en potensfunktion. Fremskrivningsfaktoren for x (F_x) er 1 + 30 % = 1,30.

   Fremskrivningsfaktoren for luftmodstanden (F_y) bliver: F_y = (F_x)² = 1,30² = 1,69.

   Dermed er den procentuelle vækst for luftmodstanden, y: (1,69 - 1)·100 % = 69 %

Svar på opgave 7:

1. Det skal i følge opgaven antages, at der sker en eksponentiel vækst, y = y₀·(1 + x)ⁿ hvor y er indbyggerantallet i 2006, b er indbyggerantallet i 1967 og n er antal år mellem 1967 og 2006 og x er den gennemsnitlige vækstrate.

   Det bemærkes, at formlen ligner kapitalformlen, blot er den gennemsnitlige rentesats skiftet ud med den gennemsnitlige vækstrate.

   Man skal løse ligningen 300 mio. = (200 mio.)·(1 + x)³⁹ med hensyn til x. Man får:

   300 mio. = (200 mio.)·(1 + x)³⁹ ⇔

   (300 mio.)/(200 mio.) = (1 + x)³⁹ ⇔

   1,5 = (1 + x)³⁹ ⇔

   ³⁹√[1,5] = ³⁹√[(1 + x)³⁹] ⇔

   ³⁹√[1,5] = 1 + x ⇔

   x = ³⁹√[1,5] - 1 ⇔

   x = 0,01045

   Dvs. den gennemsnitlige årlige vækstrate i indbyggerantallet mellem 1967 og 2006 er 0,010 = 1,0 %

Svar på opgave 8:

1. Da prisen er proportional med højde gælder: prisen for 70 mm spalteplads = [(70 mm)/(50 mm)]·(prisen for 50 mm spalteplads) = (7/5)·3450 kr. = 4.830 kr.

   Kald højden af den spalteplads, som nman kan få for 8970 kr. for x. Der gælder:

   Prisen for x mm spalteplads = (x/50)·(prisen for 50 mm spalteplads). Dette skal løses med hensyn til x, når de kendte værdier er indsat:

   8970 kr. = (x/(50 mm))·(3450 kr.) ⇔

   (8970 kr.)/(3450 kr.) = x/(50 mm) ⇔

   x = [(8970 kr.)/(3450 kr.)]·50 mm ⇔

   x = 130 mm

   Dvs. højden af den spalteplads, som man kan få for 8970 kr., er 130 mm

2. Prisen for en tofarvet spalteannonce er lig med prisen på en sort/hvid annonce med samme højde plus et fast beløb på 2710 kr.

   Det giver formlen: y = x·(3450 kr.)/(50 mm) + 2710 kr. = x·(69 kr./mm) + 2710 kr., hvor y er prisen for en annonce i to farver i kr., og x er annoncens højde i mm.