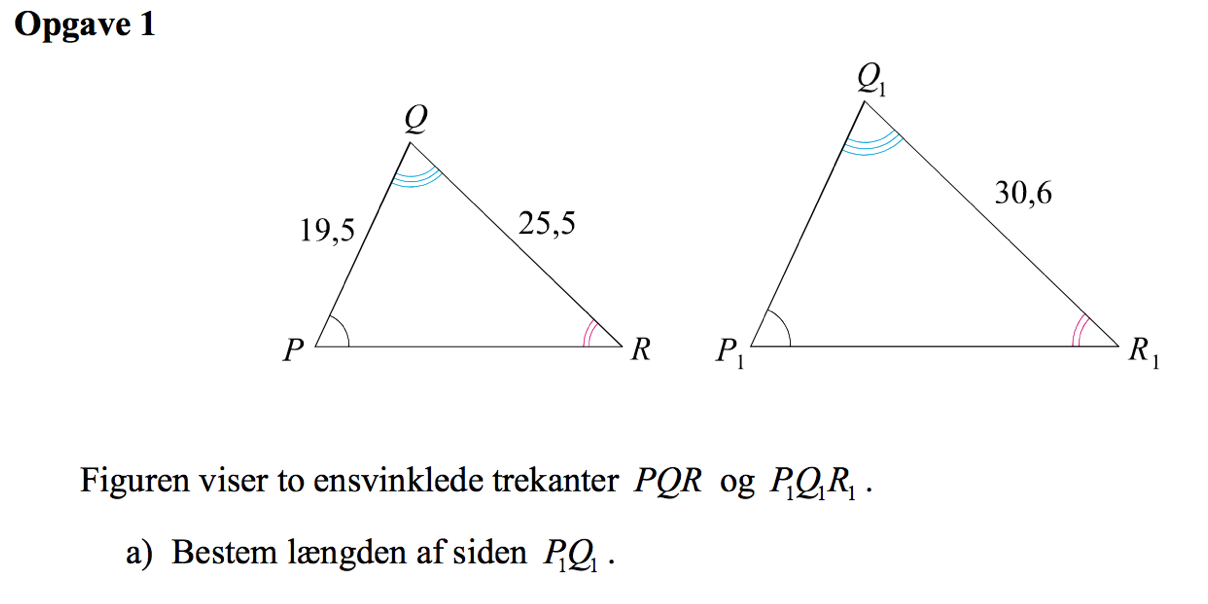
Svar på opgave 1:

1. Skaleringsfaktoren for at komme fra trekant PQR til trekant P₁Q₁R₁ er |Q₁R₁|/|QR| = 30,6/25,5 = 1,2.

   Dermed er |P₁Q₁| = 1,2·|PQ| = 1,2·19,5 = 23,4

Svar på opgave 2:

1. Man skal bruge kapitalformlen: K = K₀·(1 + r)ⁿ, hvor K₀ = 15.000 kr., r = 2,6 % = 0,026 og n = 20.

   Man får: K = 15000·1,026²⁰ = 25063,3

   Dvs. der står 25.063 kr. efter 20 år.

2. Man skal løse ligningen 15000·(1+x)²⁰ = 30000 med hensyn til x (hvor x > 0) og får i Ti-Nspire:

   solve(15000*(1+x)²⁰=30000. and x>0,x) ▸ x=0.03526

   Dvs. den årlige procentivise rentesats for banken er 0,03526 = 3,5 %

Svar på opgave 3:

1. Året 2008 svarer til x = 8. Man får derfor i følge modellen:

   1,82·8 + 0,5 = 15,06

   Dvs. at statens boligindtægter bliver 15,1 mia. kr. i 2008

2. For at beregne det år, hvor indtægterne kommer over 19 mia. kr. skal man først løse ligningen: 1,82·x + 0,5 = 19 med hensyn til x. Dette gøres i Ti-Nspire:

   solve(1.82*x+0.5=19,x) ▸ x=10.1648

   Dvs. indtægterne passerer 19 mia. kr., når der er gået 10,2 år efter 2000. Dette kan tolkes som enten, at det sker i løbet af 2010 eller som, at 2011 er det første år, hvor indtægterne har passerert 19 mia. kr. fra starten af året.

   Her vælges 2011 som det år, hvor indtægterne passerer 19 mia. kr.

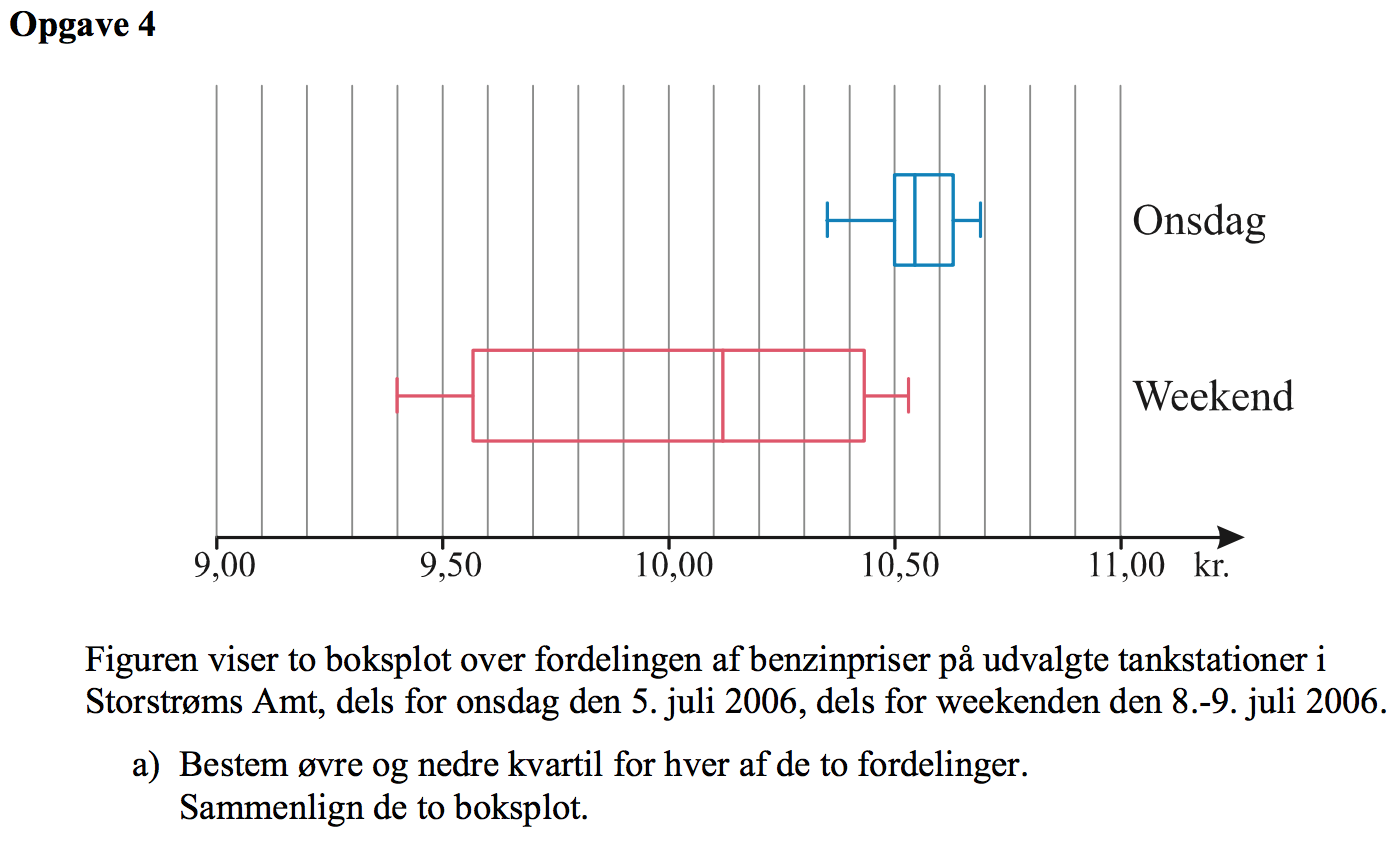
Svar på opgave 4:

1. Nedenunder er nedre og øvre kvartil indtegnet på de to boksplot.

   

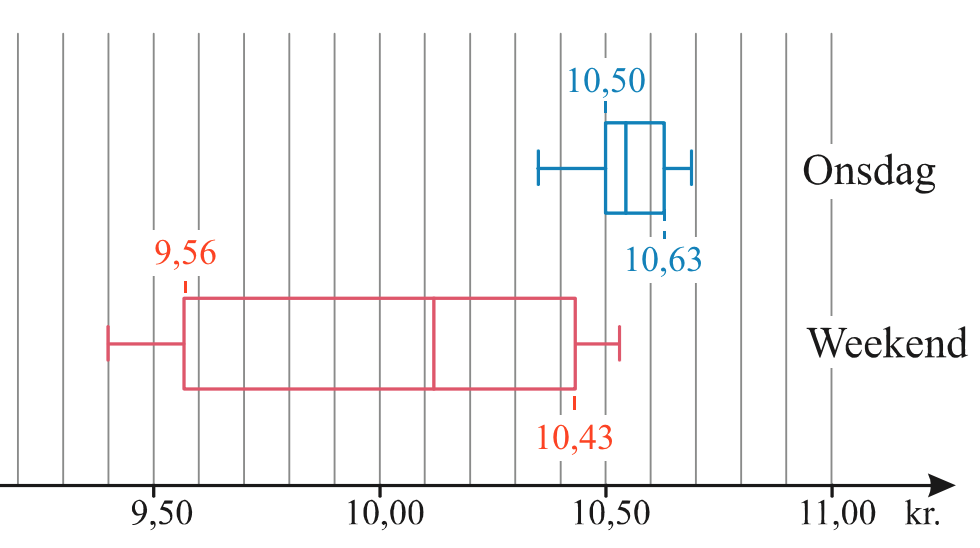
   Det ses at nedre kvartil for onsdag er 10,50, mens øvre kvartil er 10,63. Nedre kvartil for weekend er 9,56, mens øvre kvartil er 10,43

   Boksplottet for onsdag har en højere median (lodret streg midt i firkanten) og mindre variationsbredde (mindre forskel på mindste og største værdi).

   (En mulig forklaring er større efterspørgsel, der driver prisen op om onsdagen i forhold til weekenden.)

Svar på opgave 5:

1. Modellen er en lineær model, y = a·x + b, hvor y er det gennemsnitlige antal køretøjer på motorvejen i løbet af et år. x er antal år efter 1996. a er den årlige vækst i antal køretøjer som er 2460 og b er antalletaf biler i startåret 1996, som er 80.000. Dvs. modellen er

   y = 2460x + 80000

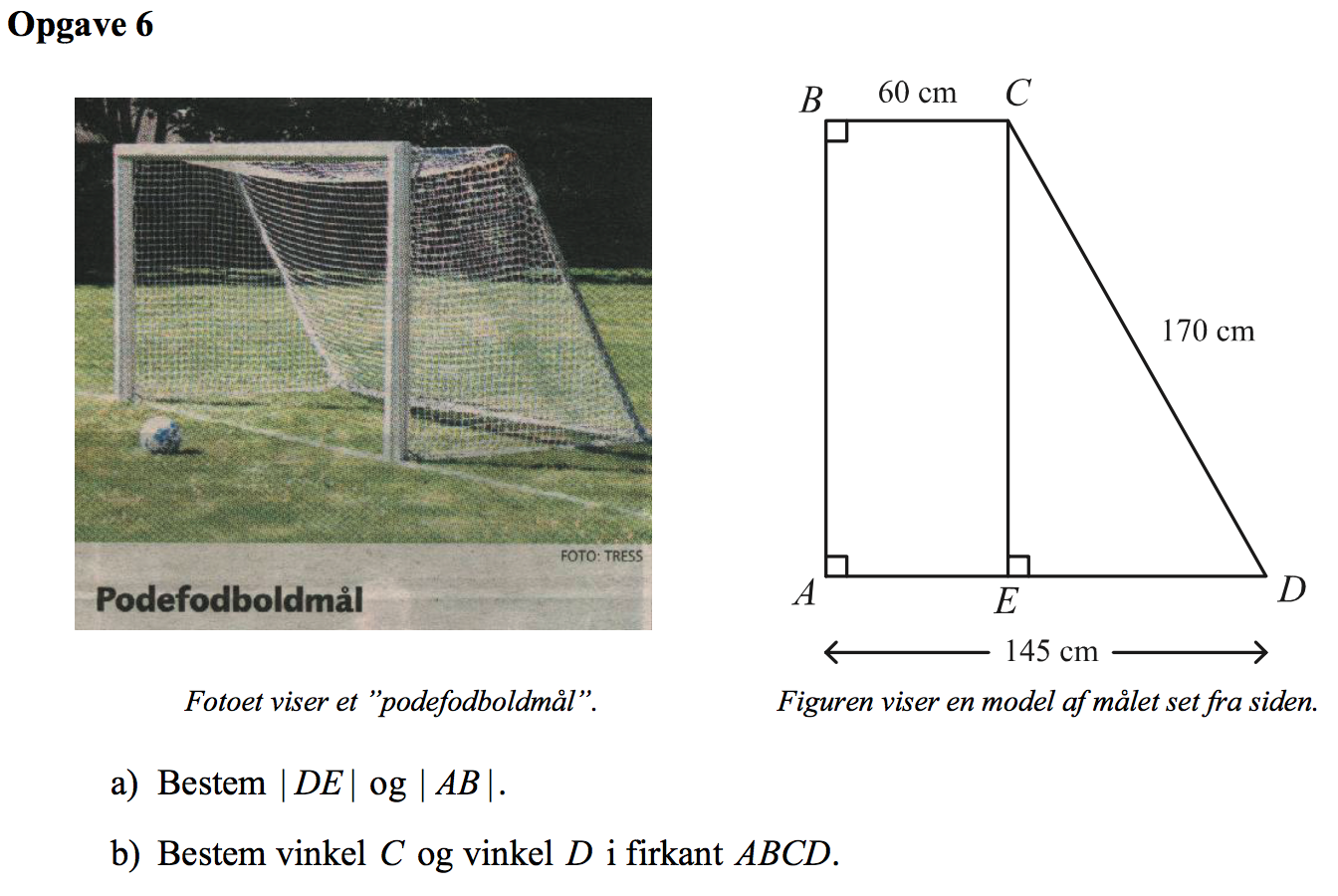
Svar på opgave 6:

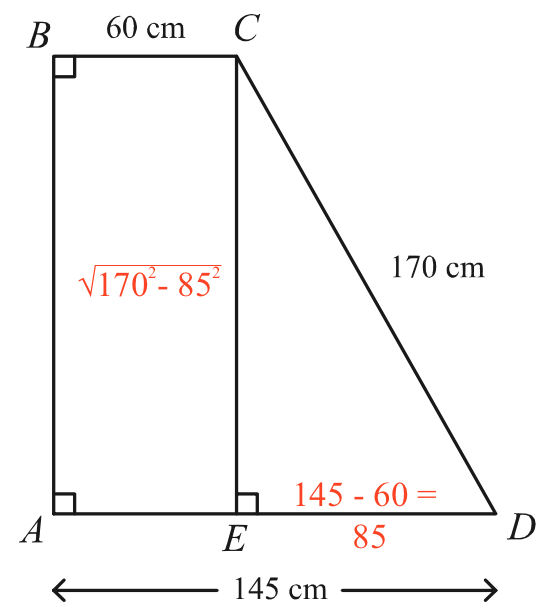
1. |DE| = |AD| - |BC| = 145 - 60 = 85. Dvs. |DE| = 85 cm

   AB har samme længde som siden CE, der er katete i den retvinklede trekant CDE. Dermed gælder i følge Pythagoras læresætning: |AB|² + |DE|² = |CD|² ⇒ |AB|² + 85² = 170². Dette løses med hensyn til |AB| i Ti-Nspire:

   solve(ab²+85²=(170.)²,ab)|x>0 ▸ ab=147.224

   Dvs. |AB| = 147,2

2. For vinklen D gælder, at den indgår i den retvinklede trekant CDE. CD er hypotenusen og CE er den modstående side til vinkel D. Dermed gælder at |CD|·cos(∠D) = |CE| ⇒ 170·cos(∠D) = 85. Dette løses med hensyn til vinkel D i Ti-Nspire:

   solve(170*cos(d*1.°)=85.,d)|0<d<90 ▸ d=60.

   Dvs. vinkel D er 60°

   Vinkel C i firkant ABCD er lig med vinkel C i firkant ABCE + vinkel C i trekant CDE.

   Vinkel C i trekant CDE (∠DCE) findes ved hjælp af reglen om at vinkelsummen i en trekant er 180°. Dvs. ∠DCE = 180° - 60° = 120°.

   Vinkel C i firkant ABCE = 90°. Dette giver at vinkel C i firkant ABCD er 60° + 90° = 150°

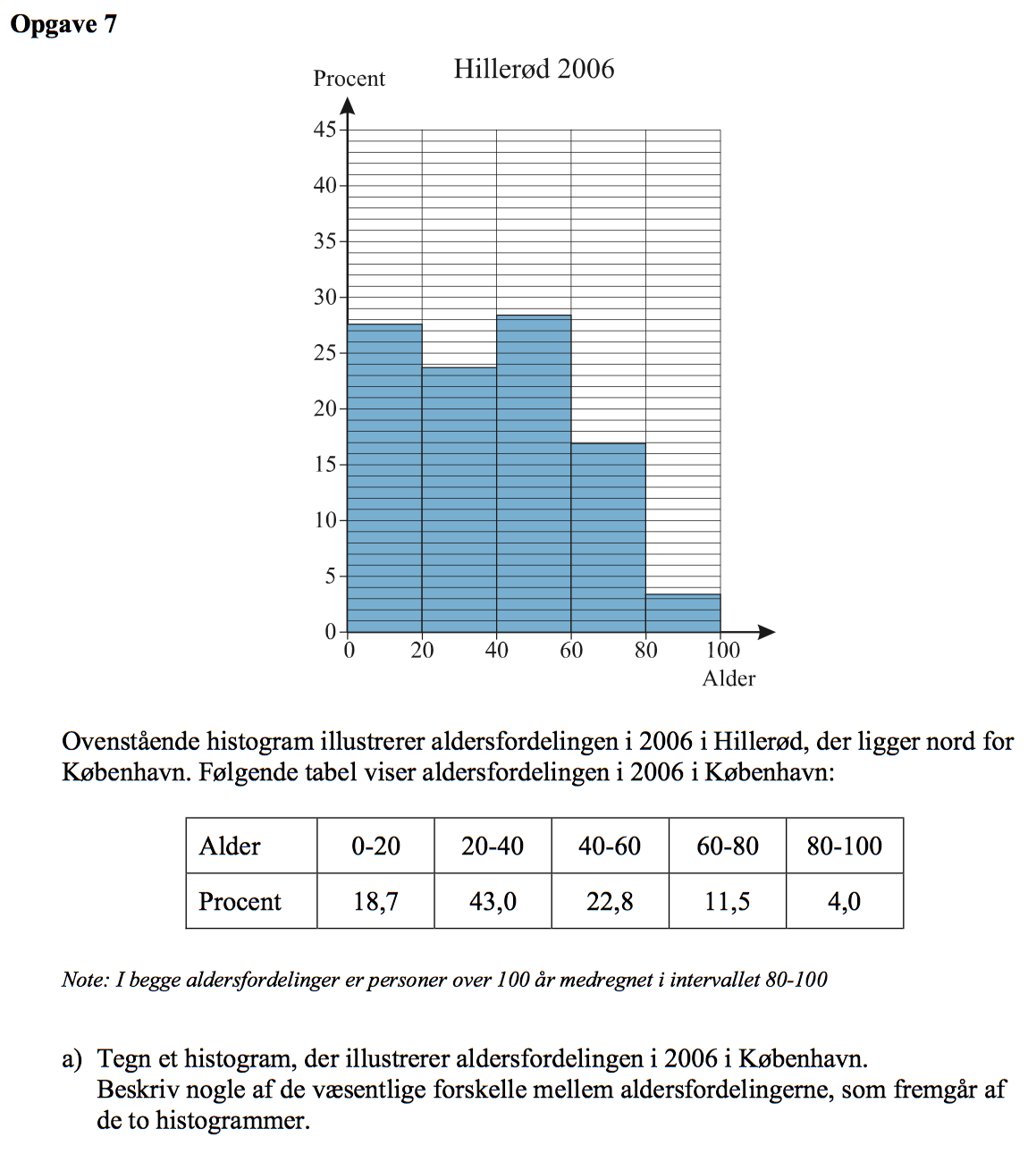
Svar på opgave 7:

1. Nedenfor er histogrammet for København og Hillerød tegnet sammen.

   

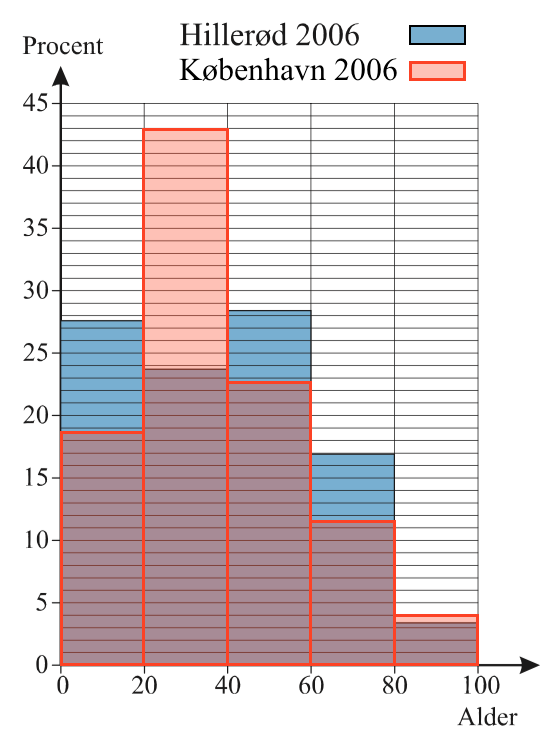
   Den væsentligste forskel er gruppen i alderen mellem 20 og 40 år. der er meget større i København end i Hillerød. Dette skyldes nok de mange studerende i København.

Svar på opgave 8:

1. Nedenfor er vist skemaet med en række for antallet af motorscykler tilføjet. Antallet i 2005 kaldes x.

   

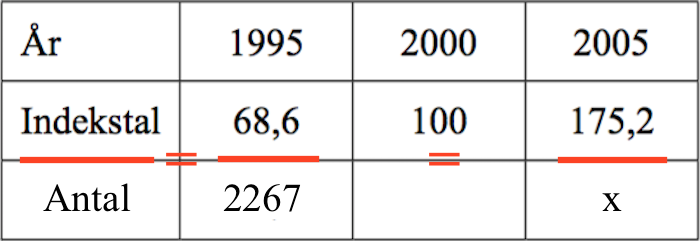
   Som antydet på figuren gælder, at forholdet mellem indeks for et år og antallet af motorcykler dette år er det samme for alle år. Man skal derfor løse ligningen: 68,6/2263 = 175,2/x med hensyn til x. Dette gøres i Ti-Nspire:

   solve((68.6/2263)=(175.2/x),x) ▸ x=5779.56

   Dvs. antallet af nyregistrerede motorcykler i 2005 er 5.780

Svar på opgave 9:

1. For at finde a og b skal man løse to ligninger med de ubekendte a og b. Disse ligninger er:

   b·a⁰ = 205 ∧ b·a^2006-1950 = 688 ⇔ b·a⁰ = 205 ∧ b·a⁵⁶ = 688.

   Disse ligninger løses i Ti-Nspire:

   solve(b*a⁰=205 and b*a⁵⁶=688.,a,b)|a>0 ▸ a=1.02186 and b=205.

   Dvs. a = 1,0219 og b = 205 mio.

2. Tallet a er fremskrivningsfaktoren, som er det tal, sidste års befolkningstal skal ganges med, for at få det nye års. Tallet b er startværdien, dvs. befolkningstallet i 1950.

3. Året 2050 svarer til x = 100. Man skal finde værdien af y for x = 100 og de fundne værdier af a og b fra første spørgsmål. Man får:

   205·(1,02186)¹⁰⁰ = 1781,94. Dvs. at antallet af mennesker, som er over 60 år gamle, i 2050 i følge modellen er 1,8 mia.. Dette passer med det faktiske antal.