Svar på opgave 1:

1. Man skal bruge kapitalformlen: K = K₀·(1 + r)ⁿ, hvor K₀ = 7000 kr., r = 3,3 % = 0,033 og n = 12. Man skal finde K:

   K = (7700 kr.)·(1,033)¹² = 11368,30 kr.

   Dvs. der står 11.368 kr. på kontoen efter 12 år.

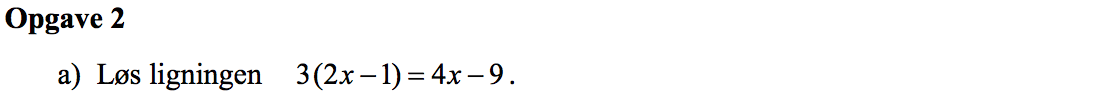
Svar på opgave 2:

1. 3·(2·x - 1) = 4·x - 9 ⇔

   6·x - 3 = 4·x - 9 ⇔

   6·x - 4·x = -9 + 3 ⇔

   2·x = -6 ⇔

   x = -3

Svar på opgave 3:

1. Der er tale om en negativ eller aftagende udvikling med et fast antal om året på 2100 fra en begyndelsesværdi på 77688.

   Dette giver den (negative) lineære model: y = -2100x + 77688, hvor y er medlemstallet for tennisforbundet og x er antal år efter 1999.

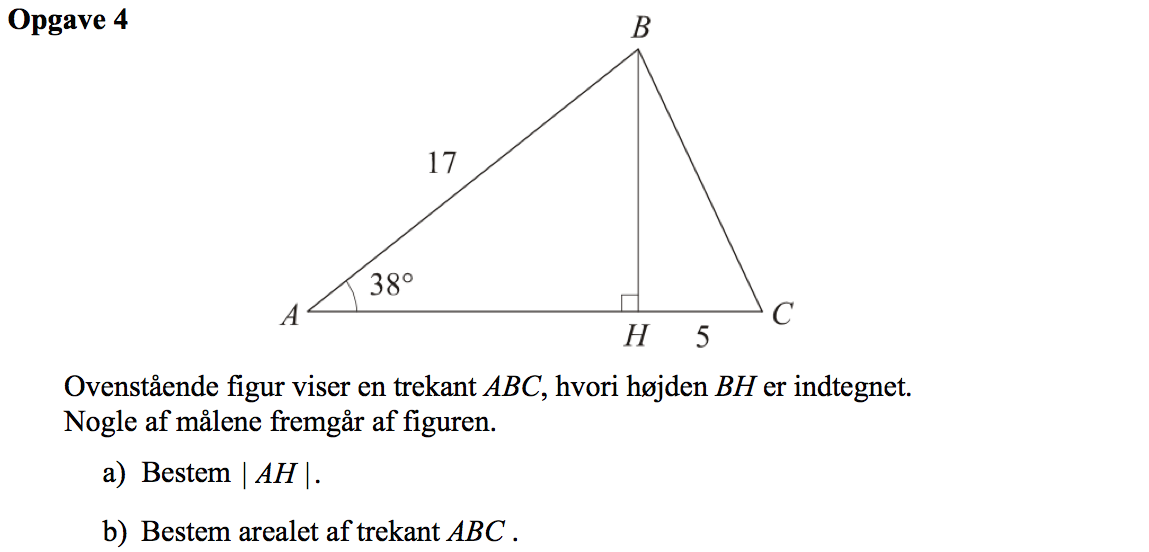
Svar på opgave 4:

1. ΔABH er retvinklet. Derfor gælder den trigonometriske formel |AH| = 17·cos(32°) = 13,4

2. Arealet af ΔABC = 0,5·grundlinje·højde =

   0,5·|AB|·|BH| =

   0,5·(|AH| + 5)·|BH| =

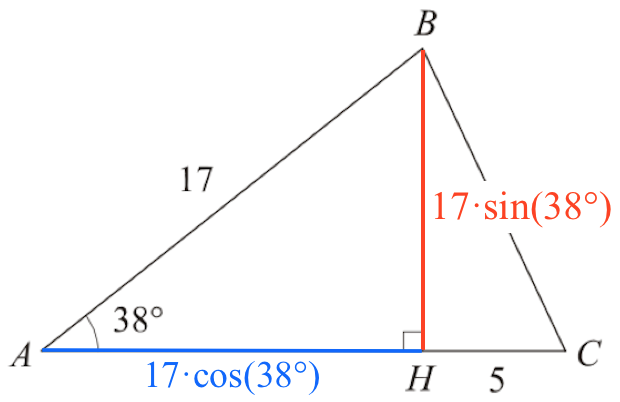
   0,5·(17·cos(32°) + 5)·(17·sin(32°)) = 96,3

   De trigonometriske formler er vist nedenunder.

   

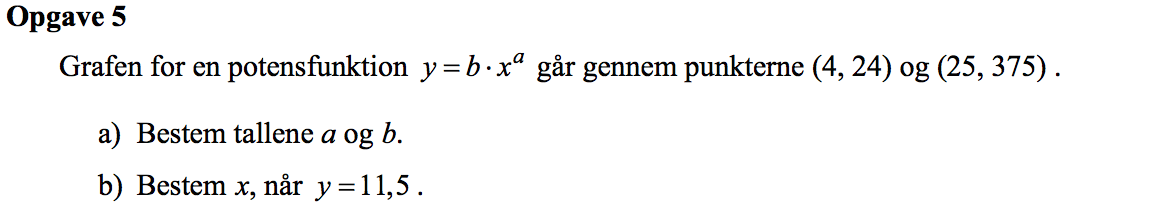
Svar på opgave 5:

1. For at bestemme a og b skal man løse de to sammenhørende ligninger: y₁ = b·(x₁)^a og y₂ = b·(x₂)^a, hvor x₁ = 4, y₁ = 24, x₂ = 25 og y₂ = 375. Man får:

   24 = b·4^a ∧ 375 = b·25^a ⇔

   b = 24/4^a ∧ 375 = (24/4^a)·25^a ⇔

   b = 24/4^a ∧ 375/24 = 25^a/4^a ⇔

   b = 24/4^a ∧ 15,625 = (25/4)^a ⇔

   b = 24/4^a ∧ 15,625 = 6,25^a ⇔

   b = 24/4^a ∧ ln(15,625) = a·ln(6,25) ⇔

   b = 24/4^a ∧ a = ln(15,625)/ln(6,25) ⇔

   b = 24/4^1,5 ∧ a = 1,5 ⇔

   a = 1,5 ∧ b = 3

   Dvs. a = 1,5 og b = 3

   Nedenunder er det samme løst i Ti-Nspire:

   

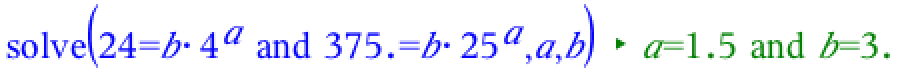
2. Man skal løse ligningen: 11,5 = 3·x^1,5. Man får:

   11,5/3 = x^1,5 ⇔

   3,83333 = x^1,5 ⇔

   ^1,5√[3,83333] = x ⇔

   x = 2,45

   Løsning i Ti-Nspire:

   

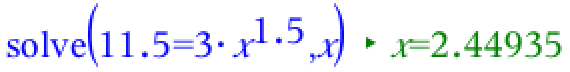
Svar på opgave 6:

1. Man udvider tabellen med en række, der indeholder priser. Prisen for 1994 kaldes x. Dette er vist nedenfor:

   

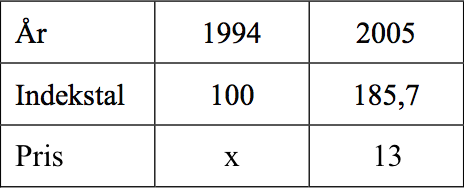
   Der gælder, at indeks/pris er ens for alle år, dvs: 100/x = 185,7/13 ⇔

   x = 100/(185,7/13) ⇔

   x = 7,0005

   Dvs. en Kung Fu is kostede 7 kr. i 1994.

Svar på opgave 7:

1. Man skal finde y(10 °C) som er 3,5·10 + 955 hektopascal = 990 hektopascal, der er lufttrykket ved en lufttemperatur på 10 °C.

   Tallet 3,5 er det antal hektopascal, som lufttrykket stiger med, hver gang temperaturen stiger en grad celsius.

Svar på opgave 8:

1. Man skal løse de sammenhørende ligninger y₁ = b·a^x₁ og y₂ = b·a^x₂ med hensyn til a og b, når

   x₁ = 0 (år 1980), y₁ = 158, x₂ = 25 (år 2005) og y₂ = 628. Man får:

   158 = b·a⁰ ∧ 628 = b·a²⁵ ⇔

   158 = b ∧ 628 = 158·a²⁵ ⇔

   158 = b ∧ 628/158 = a²⁵ ⇔

   158 = b ∧ 3,97468 = a²⁵ ⇔

   158 = b ∧ ²⁵√[3,97468] = a ⇔

   a = 1,05675 ∧ b = 158

   Dvs. a = 1,0568 og b = 158

2. Man skal først finde x i ligningen: y(x) = 2500 ⇒ 2500 = 158·1,0568^x. Man får:

   2500 = 158·1,0568^x ⇔

   ln(2500/158) = ln(1,0568^x) ⇔

   ln(2500/158) = x·ln(1,0568) ⇔

   x = ln(2500/158)/ln(1,0568) ⇔

   x = 49,99 ⇔

   Dette rundes op til 50 og man får, at 2500 personer over 100 år nås i 1980 + 50 = 2030

3. Fordoblingskonstanten er ln(2)/ln(a) år = ln(2)/ln(1,0568) år = 12,5 år

   Hvis fordoblingskonstanten er 12,5 år er firedoblingskonstanten 2·12,5 år = 25 år, så påstanden passer med modellen. (En firedobling er to på hinanden følgende fordoblinger.)

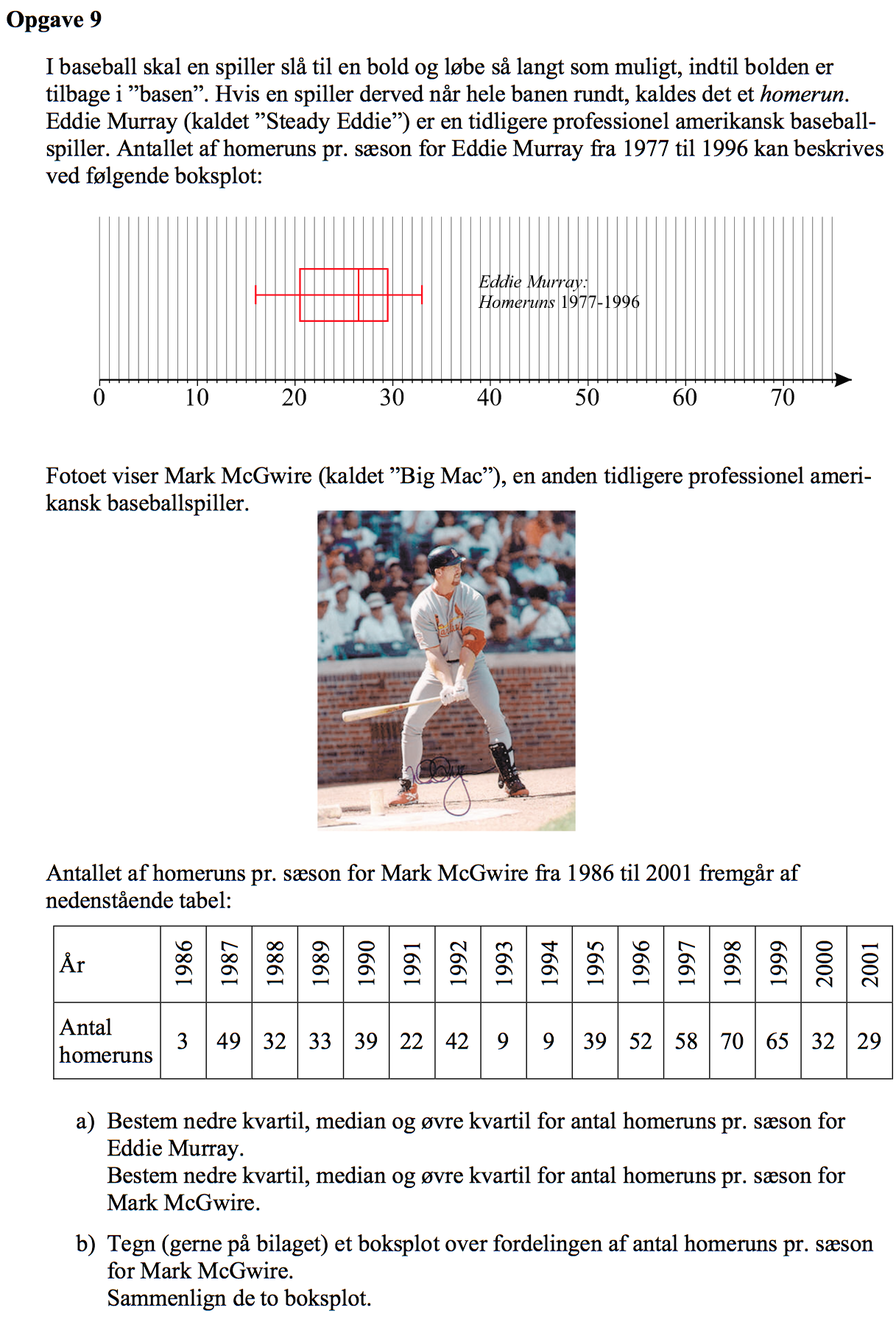
Svar på opgave 9:

1. Kvartilerne for Eddie Murray aflæses af boksplottet som vist nedenfor

   

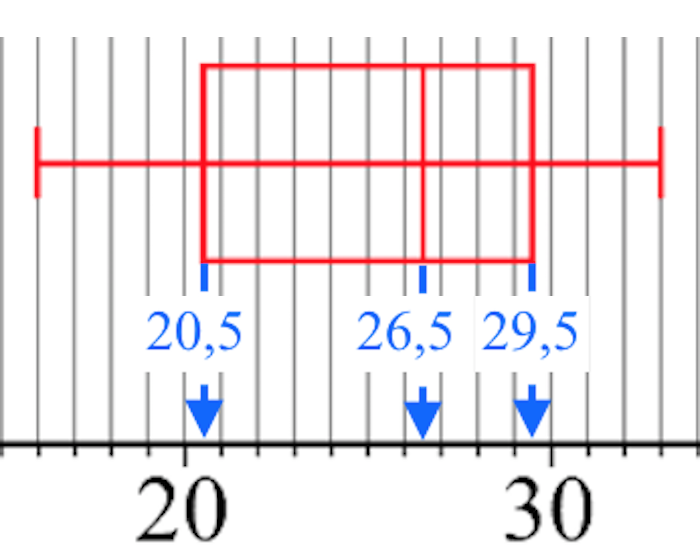
   Dvs. nedre kvartil = 20,5, median = 26,5 og øvre kvartil = 29,5

   Kvartilerne for Mark McGwire findes ved først at sortere listen af de 16 homeruns som vist:

   

   Da antallet af værdier er lige, starter man med at dele listen på midten og tage gennemsnittet af de to værdier, der ligger omkring midten. Dette gennemsnit er medianen, dvs. medianen er (33+39)/2 = 36.

   De to halvdele af listen har begge et lige antal værdier, og de deles ligesom hele listen på midten. Man tager gennemsnittet af de to midterste værdier i den venstre underliste og får nedre kvartil til (22+29)/2 = 25,5.

   Tilsvarende tager man gennemsnittet af de to midterste værdier i den højre underliste og får øvre kvartil til (49+52)/2 = 50,5.

   Kvartilerne for Mark McGwire er dermed: nedre kvartil = 25,5, median = 36 og øvre kvartil = 50,5

2. På nedenstående figur er Mark McGwires boksplot vist med blåt og Eddie Murray med rødt.

   

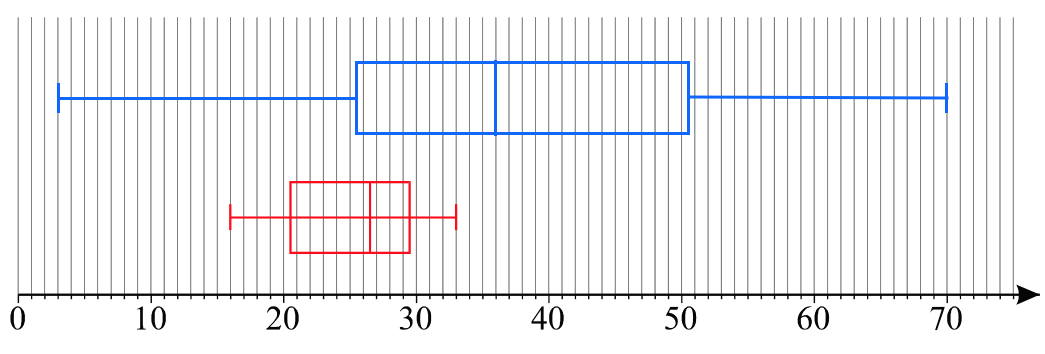
   Forskellen er, at Mark McGwire har en højere median og større variationsbredde (forskel på mindste og største værdi). Eddie Murray lever op til sit øgenavn "Steady" ved at have værdier, der ligger tæt samlet (lille variationsbredde).