Svar på opgave 1:

1. (a + b)² + 3a·(a - b) - b² =

   a² + 2ab + b² + 3a² - 3ab - b² =

   (1a² + 3a²) + (2ab - 3ab) + (1b² - 1b²) =

   (1 + 3)·a² + (2 - 3)·ab + (1 - 1)·b² =

   4a² + (-1)·ab - 0b² =

   4a² - ab

Svar på opgave 2:

1. Man skal løse ligningen f(x) = g(x) med hensyn til x og derefter indsætte den fundne værdi af x i f(x) for at finde den tilhørende y-værdi for skæringspunktet. Man får:

   f(x) = g(x) ⇒

   2x - 5 = -2x + 11 ⇔

   2x + 2x = 11 + 5 ⇔

   4x = 16 ⇔

   x = 16/4 = 4

   Dvs. x-koordinaten for skæringspunktet for graferne til f og g er x = 4. Den tilhørende y-koordinat er f(4) = 2·4 - 5 = 3.

   Dvs. skæringspunktet for graferne til f og g er (x,y) = (4,3)

Svar på opgave 3:

Figuren med graferne er gentaget nedenunder som hjælp.



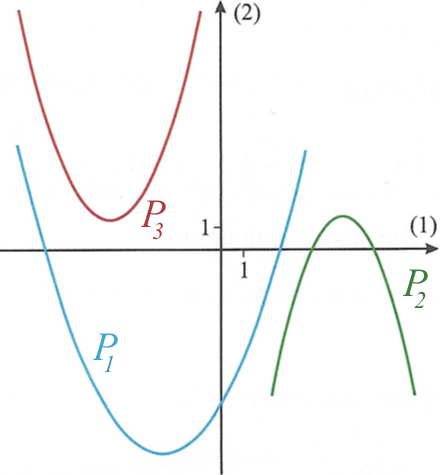
1. Koefficienten a er positiv for P1 og P3. Det skyldes, at de vender grenene opad, hvilket svarer til at a er positiv.

   Diskriminanten, d, er negativ for P1 og P2. Det skyldes, at disse grafer hver skærer x-aksen i to punkter, hvilket svarer til, at diskriminanten er positiv for andengradspolynomierne.

Svar på opgave 4:

1. Modellen er f(x) = 47295·1,017^x, hvor x er antal år efter 2005.

   Dette skyldes, at der er tale om en eksponentiel funktion, idet der er en årlig procentvis vækst på 1,7 % = 0,017 og startværdien (for x = 0) er 47295.

Svar på opgave 5:

1. Da p og T er ligefremt proportionale gælder, at p/T er konstant for alle kolonner i tabellen. I den midterste kolonne ses, at p/T = 100/300 = 1/3. Dette bruges til at udfylde tabellen:

   

Svar på opgave 6:

1. Samtlige stamfunktioner er lig med det ubestemte integrale til f. Man benytter at det ubestemte integrale til e^x = e^x + konstant og det ubestemte integrale til 1/x = ln(x) + konstant (for x>0). Man får:

   

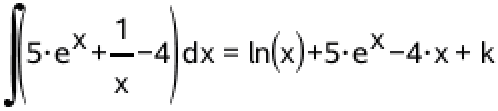
   Dvs. samtlige stamfunktioner (for x>0) er ln(x) + 5e^x - 4x + k, hvor k er en konstant.

Svar på opgave 7:

1. Man opretter lister med tider og hastigher:

   tid:={0,1,3,5,7,9,11} ▸ {0,1,3,5,7,9,11}

   hastighed:={0,3,7,12,16,23,27} ▸ {0,3,7,12,16,23,27}

   

   Af resultatet ses, at a = 2,453 og b = -0,0453

   (a fra opgaven kaldes "m" i Ti-Nspire)

2. For at finde tidspunktet skal man løse ligningen f1(x) = 50, hvor f1(x) er den regressionsfunktion som Ti-NSpire opretter.

   solve(f1(x)=50,x) ▸ x=20.3995

   Dvs. det tager 20,4 sek. før rakettens hastighed er 50 m/s.

3. Man bestemmer højden ved hjælp af integralet:

   

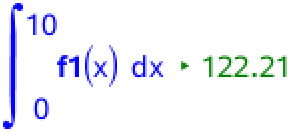
   Højden er dermed 122 m

Svar på opgave 8:

1. Først oprettes funktionen f:

   f(x):=3*x*ln(x)-x² ▸ Udført

   Dernæst bestemmes f´(x):

   derivative(f(x),x) ▸ 3*ln(x)-2*x+3

   Ligningen for tangenten til f gennem punktet P = (1,f(1)) er: y = f´(1)·(x - 1) + f(1). Man finder:

   derivative(f(x),x)|x=1 ▸ 1 (f´(1) = 1)

   f(1) ▸ −1 (f(1) = -1)

   Dette giver følgende ligning for tangenten: y = 1·(x - 1) - 1 = y = x -2

   (Ti-NSpire: y=tangentLine(f(x),x,1) ▸ y=x-2)

   Nedenunder er noget af grafen for f tegnet i Ti-NSpire:

   

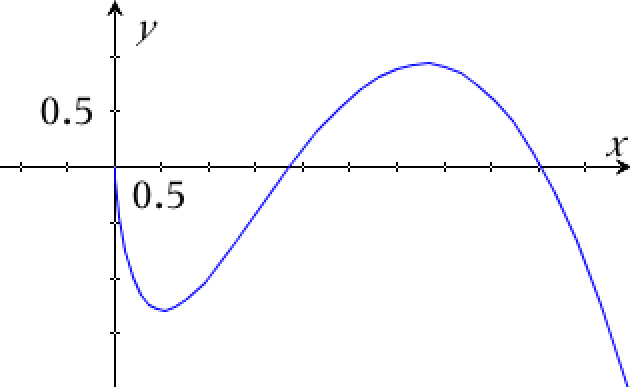
2. Monotoniforholdene for f findes ved hjælp af en fortegnsbestemmelse for f´(x). Først finder man de x, hvor f´(x) = 0:

   solve(derivative(f(x),x)=0,x) ▸ x=0.520472 or x=3.28325

   Dernæst undersøger man fortegn for f´(x) omkring disse x-værdier (forklaring med blåt):

   derivative(f(x),x)|x=0.5 ▸ −0.079442 (f´(x)<0 for x<0,520472)

   derivative(f(x),x)|x=1 ▸ 1 (f´(x)>0 for 0,520472<x<3,28325)

   derivative(f(x),x)|x=4. ▸ −0.841117 (f´(x)<0 for x>3,28325)

   Dermed er monotoniforholdene:

   f er aftagende for x<0,520, f er voksende for 0,520<x<3,28 og f er aftagende for x>3,28

Svar på opgave 9:

1. Man opretter R(x):

   r(x):=17*x^1/3 ▸ Udført

   Radius af et hulrum der fremkommer ved en sprængkraft på 8 kiloton er lig med R(8):

   r(8) ▸ 34

   Dvs. radius af hullet er 34 m

   Den sprængkraft, der er nødvendig for at skabe et hulrum med 40 m i radius, findes som løsningen til ligningen R(x)=40. Man får:

   solve(r(x)=40.,x) ▸ x=13.0267

   Dvs. den nødvendige sprængkraft er 13 kiloton

2. Man skal bruge procent-procent vækst formlen for potensfunktioner: (1 + r_y) = (1 + r_x)^a, hvor er r_y er den procentvise vækst for y (her radius), r_x = 40 % er den procentvise vækst for x (her sprængkraft) og a = 1/3 er potensfunktionens eksponent. Dette giver for r_y:

   (1 + r_y) = (1 + 40 %)^1/3 ⇔ r_y = 1,40^1/3 - 1 ⇔ r_y = (1,4^1/3 - 1)·100 % = 11,87 %

   Dvs. den procentvise vækst af hulrummets radius ved en vækst i sprængkraften på 40 % er 12 %

Svar på opgave 10:

1. |BC| findes ved hjælp af en cosinusrelation:

   solve(cos(51.°)=(88²+36²-bc²)/(2*88*36),bc)|bc>0 ▸ bc=71.0818

   Dvs. |BC| = 71,1 cm

2. Man starter med at finde arealet af ΔCDE. Dette findes ved at trække arealet af ΔABC fra 1680.

   Arealet af ΔABC er 0,5·grundlinje·(højde i B) = 0,5·88·(36·sin(51.°)) = 1231.

   Dermed er arealet af ΔCDE: 1680 - 1231 = 449.

   Det samme areal kan bestemmes ved hjælp af formlen:

   ΔCDE = 0,5·|DC|·(højde i E) = 0,5·64·(16·sin(∠D)) = 512·sin(∠D).

   Dette giver ligningen 512·sin(∠D) = 449, der løses med hensyn til (den spidse) ∠D:

   solve(512*sin(d*1.°)=449,d)|0<d<90 ▸ d=61.277

   Dvs. vinkel D = 61,3°

Svar på opgave 11:

1. Man opretter N(t):

   n(t):=15000*1.021^t ▸ Udført

   Man finder N'(10):

   derivative(n(t),t)|t=10 ▸ 383.749

   Dvs. N'(10) = 384. Dette tal er bakteriernes væksthastighed (i antal/min.) efter 10 minutter.

2. Fordoblingstiden for antallet af bakterier følger formlen ln(2)/ln(a) = ln(2)/ln(1,021) = 33,3524. Her er a grundtallet i eksponentielfunktionen N'(t).

   Dvs. fordoblingskonstanten er 33,4 min.

3. Den anden bakteries vækst følger en eksponentielfunktion: y = b·a^t, hvor a og b er ukendte. Man ved følgende om to givne tidspunkter T og T + 80:

   b·a^T = 15000 og b·a^T+80 = 95000. Den anden ligning kan omskrives til: b·a^T·b·a⁸⁰ = 95000.

   Heri indsættes højre side af den første ligning: 15000·a⁸⁰ = 95000 ⇔ a⁸⁰ = ⇔ a = ⁸⁰√[95000/15000] ⇒ a = 1,02334, idet a>0.

   Fordoblingstiden bliver for den anden bakterie er: ln(2)/ln(1,02334) min. = 30,0 min.

Svar på opgave 12:

1. Kassens rumgang, V(x), er højde·grundflade = højde·længde·bredde. Kassens højde er x. Grundfladen er den blå firkant. Dennes bredde er 60-2x og længden er 80-x. Dette giver volumenet:

   V(x) = x·(80-x)·(60-2x)

   x kan ikke være negativ, da det er en længde.

   x kan heller ikke være større end 30 cm, da kassens bredde skal være større end nul. Man får nemlig: bredde = 60 cm - 2x > 0 ⇒ x < 30 cm.

2. Man opretter V(x) som funktion:

   v(x):=x*(80-x)*(60-2*x) ▸ Udført

   Den største værdi af V(x) fås enten i endepunkterne x=0 henholdsvis x=30 eller i x-værdier, hvor V'(x) = 0. Man finder sidstnævnte:

   solve(derivative(v(x),x)=0,x)|0<x<30 ▸ x=40/3 (V'(x) er lig med 0 for x=40/3)

   Man undersøger nu værdien af V(x) for x = 0, x = 40/3 og x = 30 og får:

   v(0) ▸ 0

   v(40./3) ▸ 29629.6

   v(30) ▸ 0

   Dvs. det største rumfang af kassen fås for x = 40/3 cm = 13,3 cm

   (Ti-NSpire: fMax(v(x),x)|0<x<30 ▸ x=40/3)