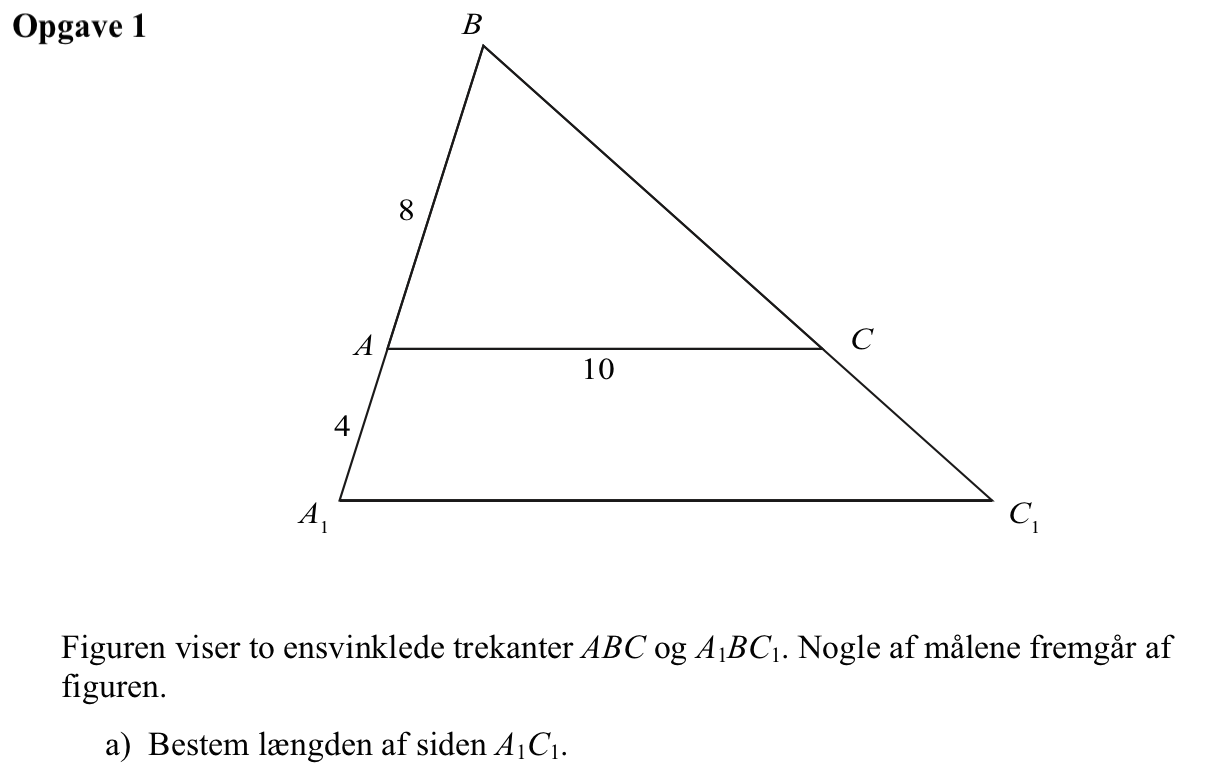
Svar på opgave 1:

1. Skaleringsfaktoren mellem trekanterne ABC og A₁BC₁ er:

   |BA₁|/|BA| = (8 + 4)/8 = 1,5 (ikke 8/4 = 2, det er fælden).

   |A₁C₁| = 1,5·|AC| = 1,5·10 = 15

Svar på opgave 2:

1. Der er tale om lineær positiv vækst (eller lineær positiv udvikling). Man sætter:

   f(x) = mængden af økologiske fødevarer i mio. kg.

   x er antal år efter 2004. Modellen bliver:

   f(x) = x·20 + 155

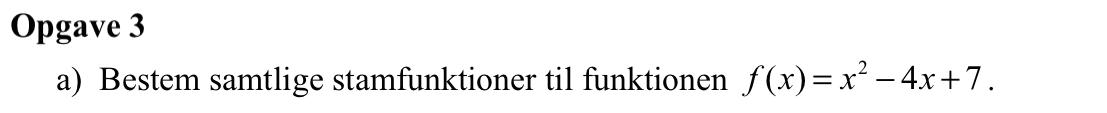
Svar på opgave 3:

1. Samtlige stamfunktioner er:

   

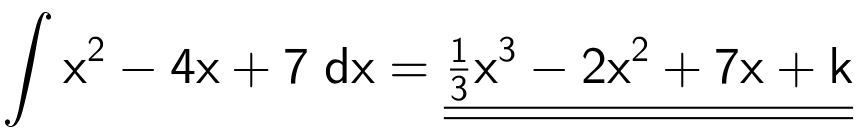
   hvor k ∈ R.

Svar på opgave 4:

1. Tangentens ligning er: y = f´(1)·(x - 1) + f(1), hvor f´(x) = 6x, dvs.:

   y = (6·1)·(x - 1) + (3·1² + 5) ⇒

   y = 6x - 6 + 8 ⇒

   y = 6x + 2

Svar på opgave 5:

1. f er lineær, g vokser eksponentielt og h aftager eksponentielt. Alle funktioner går gennem (0,3).

   Grafen er ikke lineær og ikke aftagende, derfor er den graf for g

Svar på opgave 6:

1. Andengradsliningen ax² + bx + c har netop en løsning, når diskriminanten D = 0.

   D = b² - 4·a·c = (-6)² - 4·3·c = 36 - 12c. Dvs:

   D = 0 ⇒ 36 - 12c = 0 ⇒ c = 3

   Dvs. at c skal være lig med 3, for at andengradsligningen har netop een løsning

Svar på opgave 7:

1. Man opretter to lister i Ti-Nspire:

   uger:={1,3,5,7,9} ▸ {1,3,5,7,9}

   indtjening:={43.7,24.9,15.,10.6,5.} ▸ {43.7,24.9,15.,10.6,5.}

   Dernæst anvender man kommandoen: Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Eksponentiel regression... og vælger de to lister som henholdsvis x- og y-liste:

   

   Det giver som vist (idet man vender om på a og b): a = 0,771 og b = 56,3

2. Halveringskonstanten er [ln(1/2)]/[ln(0,771)] = 2,67

   Tallet fortæller hvor mange uger, der går før uge-indtjeningen er halveret.

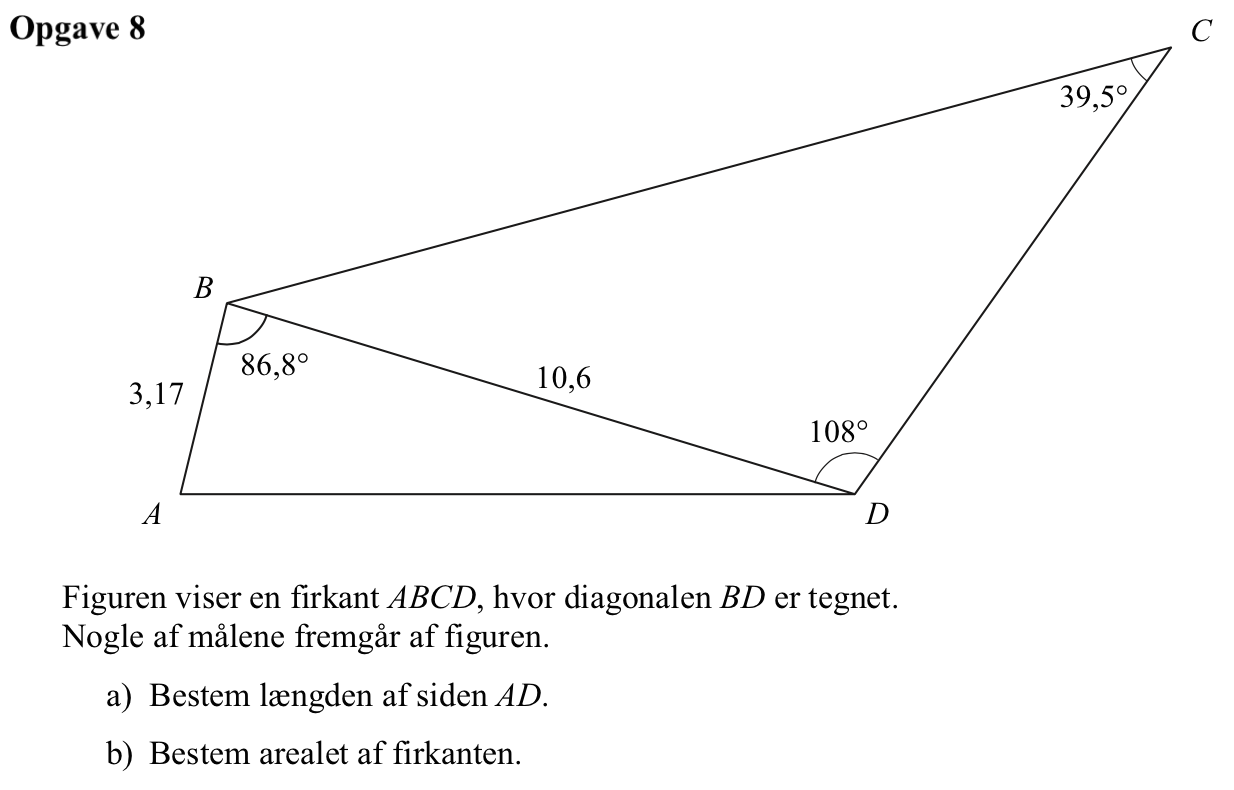
Svar på opgave 8:

1. Man finder |AD| ved hjælp af cosinusrelationen, idet |AD| kaldes x:

   

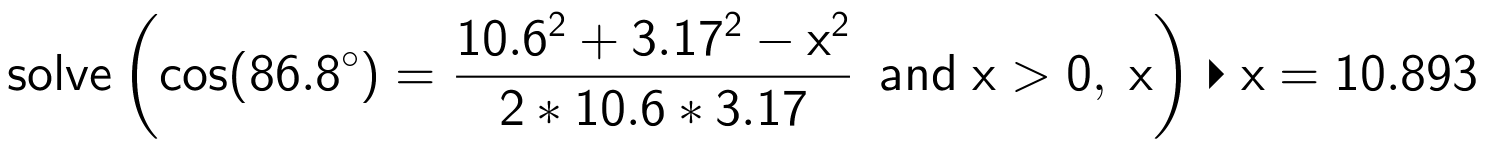
   Det ses at |AD| = 10,9

2. Arealet af trekant ABD findes i Ti-Nspire:

   0.5*10.6*3.17*sin(86.8°) ▸ 16.7748

   For at finde arealet af trekant BCD finder man først |BD| ved hjælp af sinusrelationen. Beregningen foretages i Ti-Nspire, hvor |BD| kaldes x:

   

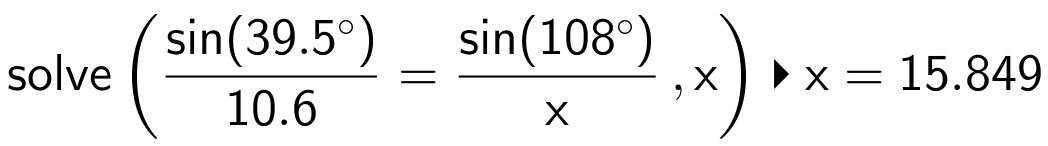
   Man finder arealet af trekant BCD til:

   0.5*15.849*10.6*sin(180°-108°-39.5°) ▸ 45.133

   Arealet af firkanten bliver summen af arealerne af de to trekanter:

   16,7748 + 45,133 = 61,9

Svar på opgave 9:

1. Den kan blive y = 17,6·0,1^0,20 år = 11,1 år

2. Vægten af A kaldes x_A og vægten af B kaldes x_B. Der gælder at x_A = 5·x_B. Levealderen for A er 17,6·(5·x_B)^0,20, mens levealderen for B er 17,6·(x_B)^0,20.

   Den procentdel, som A vil kunne leve længere end B, bliver:

   

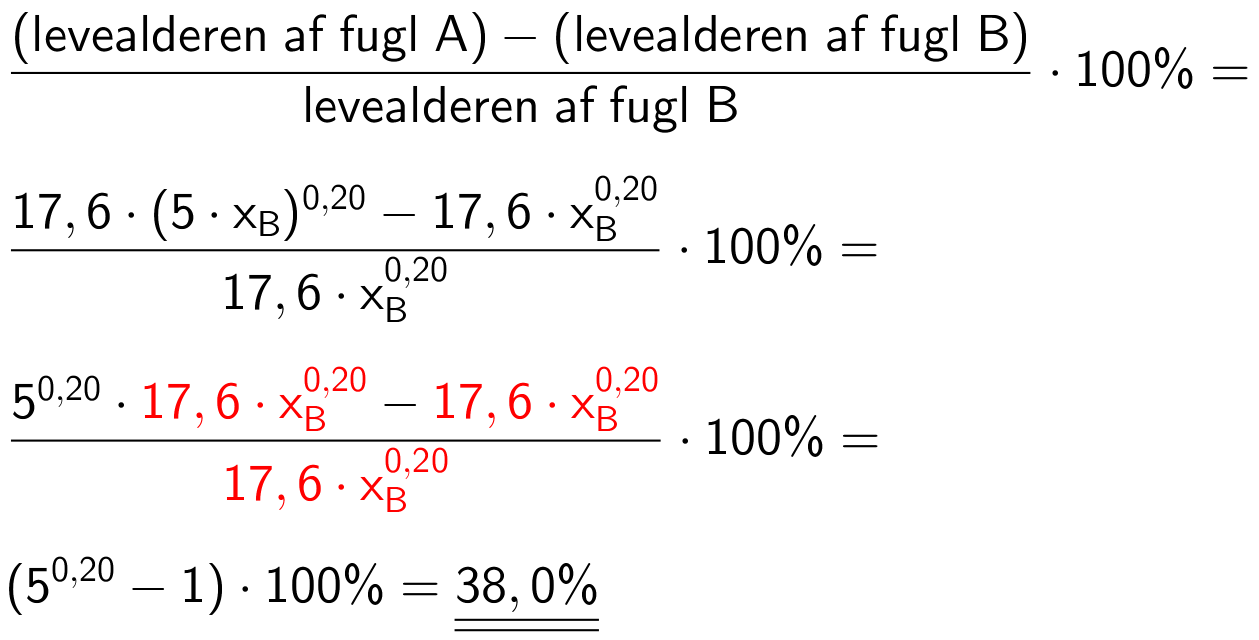
Svar på opgave 10:

1. Højden er lig med c = 6,15

   Bredden er lig med afstanden mellem rødderne, som kaldes x₁ og x₂, dvs. bredden er |x₁ - x₂|. Rødderne findes ved at løse ligningen: -0,177x² + 6,15 = 0 ⇒ x₁ = −5.89 og x₂ = 5.89.

   Bredden bliver: |x₁ - x₂| = |-5.89 - 5.89| = 11.8

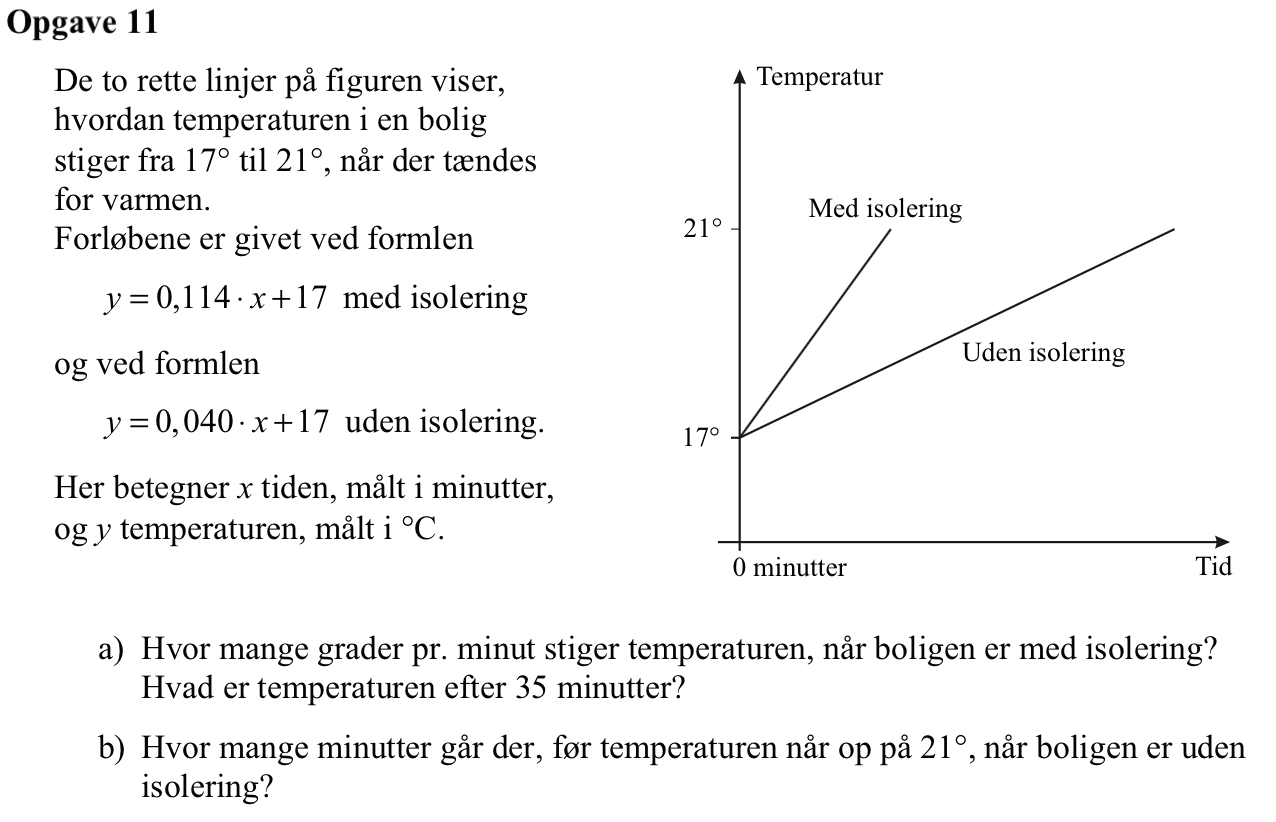
Svar på opgave 11:

1. Den stiger 0,114 grader pr. minut med isolering

   Temperaturen efter 35 minutter er 0,114·35 + 17 = 21°

2. Man skal løse ligningen: 0,040·x + 17 = 21. Man får:

   0,040·x + 17 = 21 ⇒ x = (21 - 17)/0,040 = 100, dvs. der går 100 minutter

Svar på opgave 12:

1. Man definerer f(x) i Ti-Nspire:

   

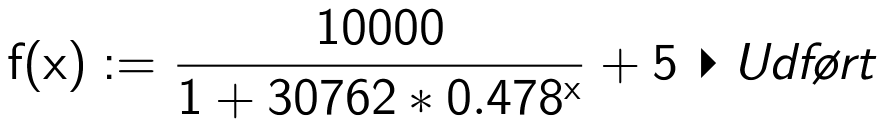
   Vægten findes med kommandoen:

   f(14) ▸ 5004.97

   Dvs. en 14 år gammel T-rex vejer 5005 kg

2. Derefter differentierer man f(x) og indsætter samtidig x = 14:

   

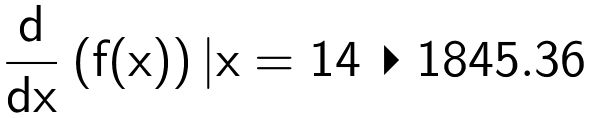
   Dvs. f´(14) = 1845 kg/år, som er T-rex'ens væksthastighed som 14-årig.

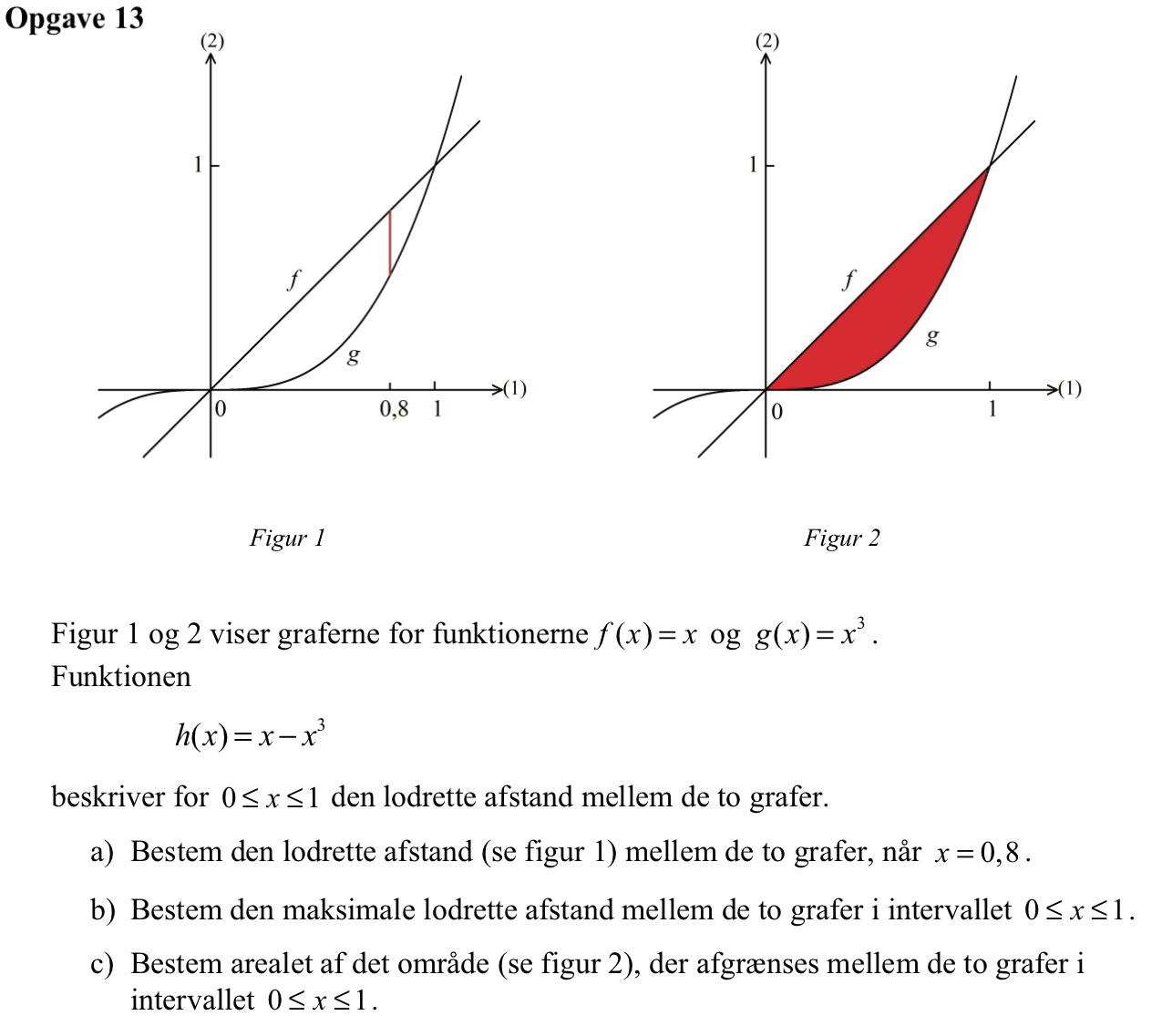
Svar på opgave 13:

1. Den lodrette afstand er h(0,8) = 0,8 - 0,8³ = 0,288

2. Man skal finde maksimum værdien af h(x). Man bruger Ti-Nspire kommandoerne:

   h(x):= x - x³ ▸ Udført

   fMax(h(x)*1.,x)|0≤x≤1 ▸ x=0.57735

   h(0.57735) ▸ 0.3849

   Det viser at den største afstand er 0,3849

3. Arealet findes med Ti-Nspire kommandoen:

   

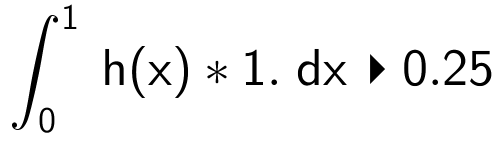
   Dvs. arealet mellem graferne er 0,25