Svar på opgave 1:

1. Man gør prøve:

   Venstre side: 23 + 3·4 = 11

   Højre side: 11

   Det ses at prøve stemmer og dermed er x = 4 en løsning.

Svar på opgave 2:

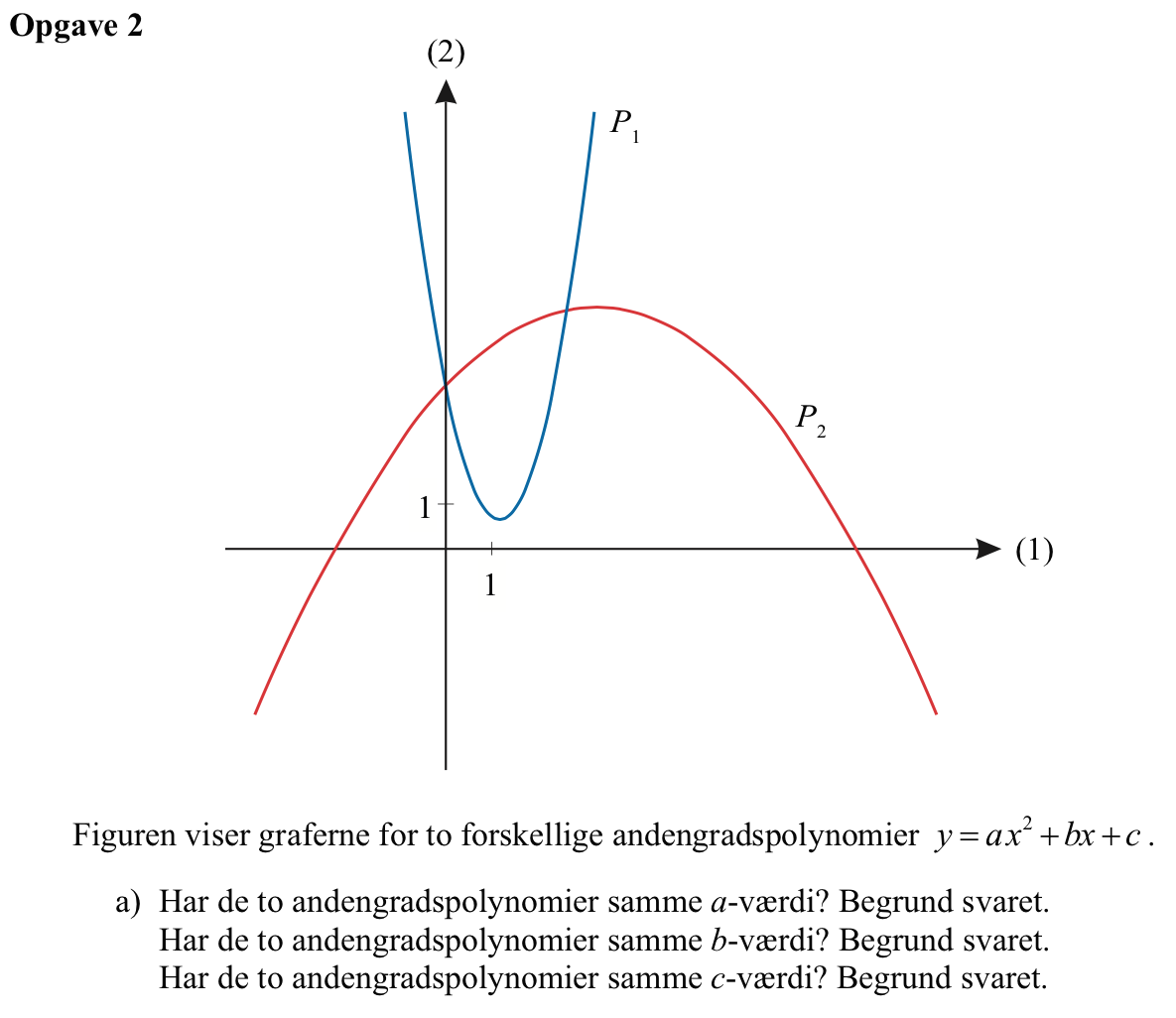
1. a er forskellig for de to andengradspolynomier idet deres grene vender hver sin vej og de har hver sin krumning

   b er også forskellig for de to andengradspolynomier, idet de har hver sin hældning for x = 0.

   c er ens for de to andengradspolynomier, idet de har samme skæringspunkt med anden-aksen.

Svar på opgave 3:

1. Der er tale om en funktion på formen b·a^x, dvs. eksponentiel vækst. Den er desuden aftagende,da a < 1.

   2,7 mio. kr. er startværdien for x = 0, dvs. værdien i år 2008 og 0,96 er fremskrivningsfaktoren, dvs. det tal, som man skal gange sidste års værdi med for at få det nye års værdi.

Svar på opgave 4:

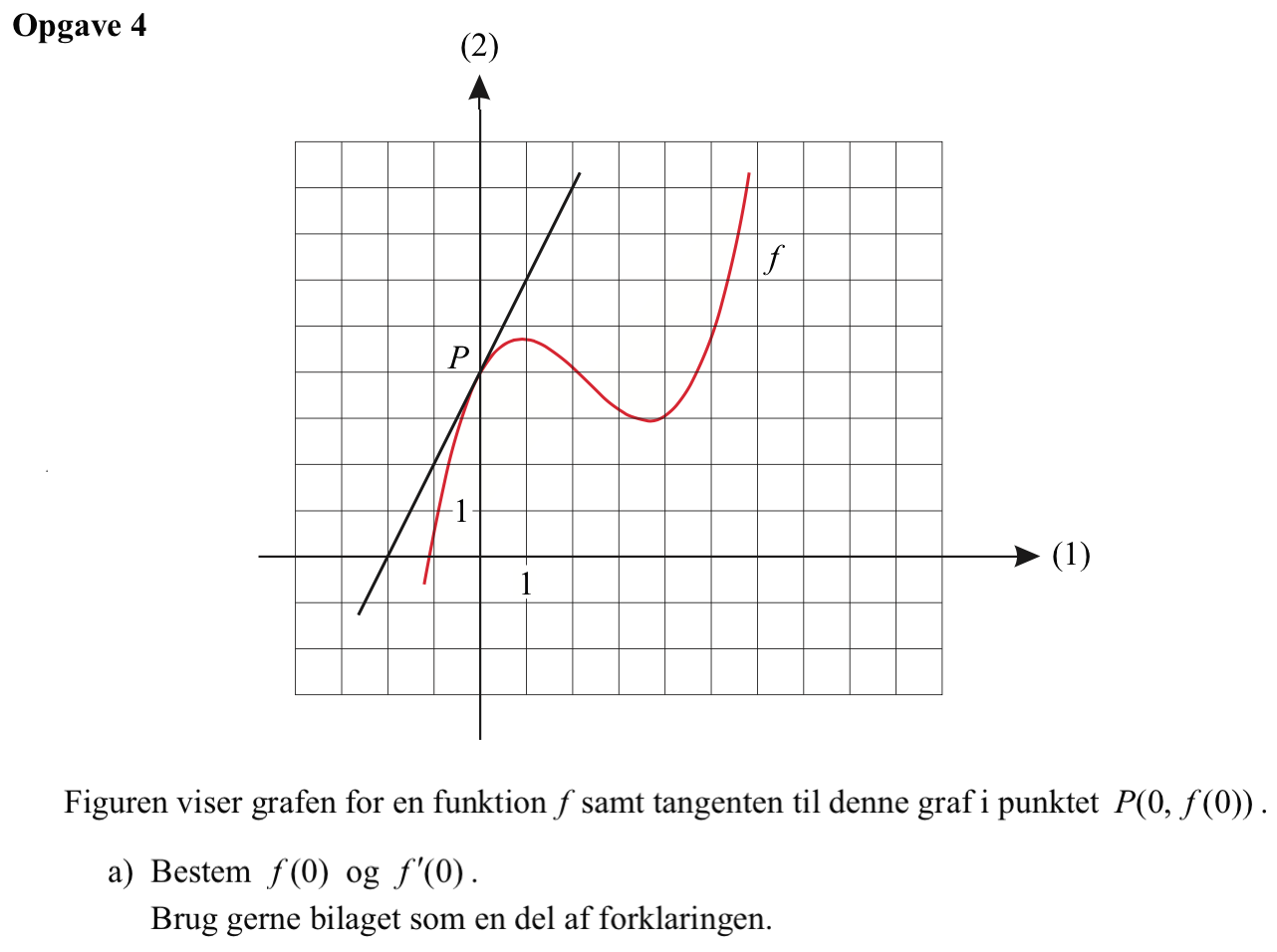
1. f(0) aflæses til 4 (skæringspunktet med 2.-aksen) og tangentens hældning aflæses til 2 (man går to tern op for hver gang man går to tern hen på linjen).

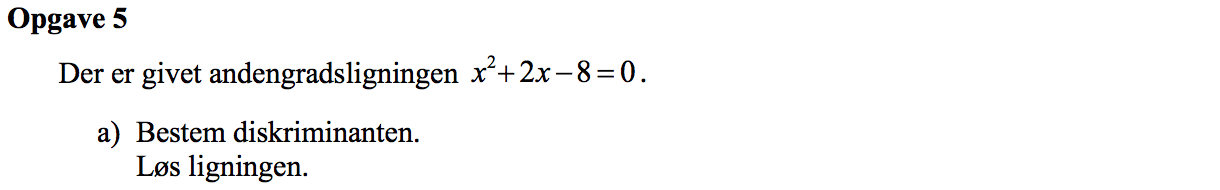
Svar på opgave 5:

1. Diskriminaten er D = 2² - 4·(1)·(-8) = 36

   Løsning: x = (-2 ± √[36])/2 ⇒ x = -4 ∨ x = 2

Svar på opgave 6:

1. Det ubestemte integrale bliver

   

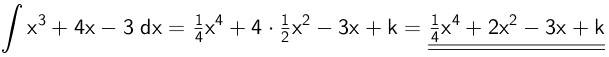
Svar på opgave 7:

1. Løsning i Geogebra. Man laver en potens-regressionsanalyse og får følgende kurve:

   

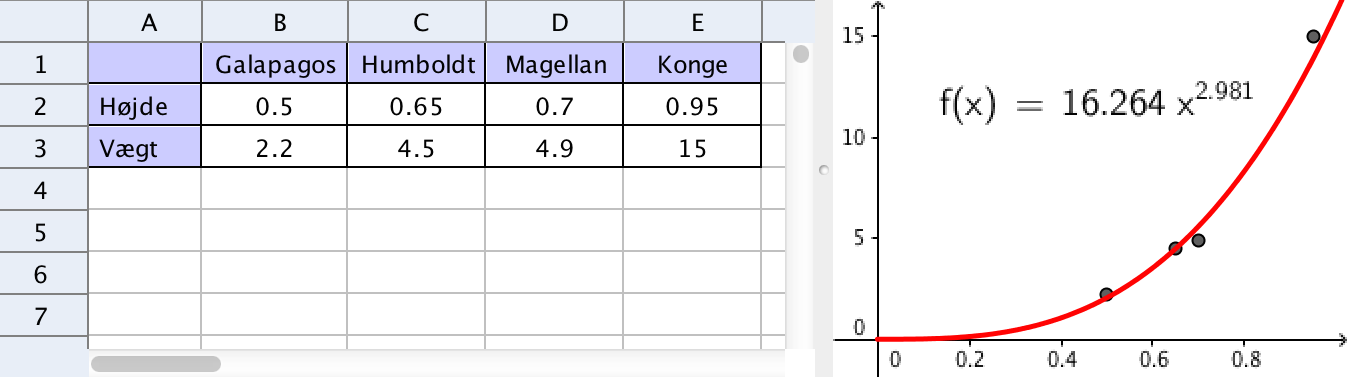
   Det giver som vist: a = 2,981 og b = 16,26

2. I følge modellen bliver kejserpingvinens vægt: 16,26·(1,2)^2,981 = 28 kg. Dvs. kejserpingvinen passer ikke med modellen!

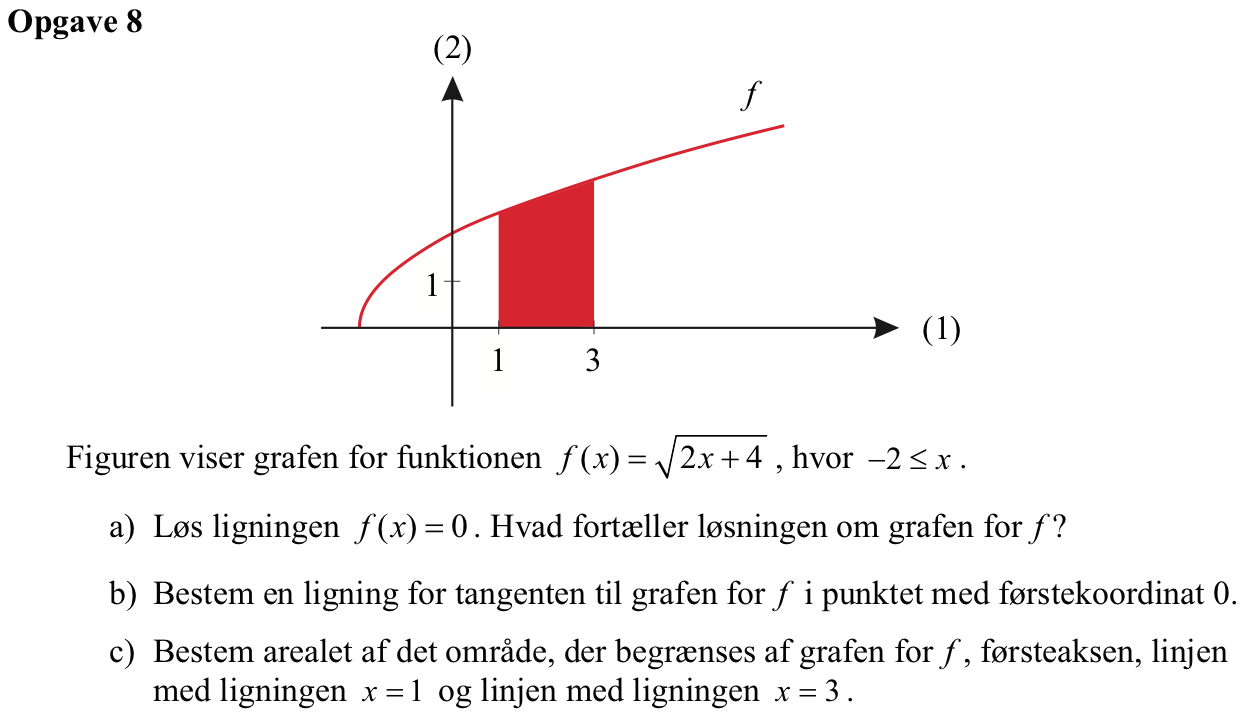
Svar på opgave 8:

1. f(x) = 0 ⇒ √[2x + 4] = 0 ⇒ 2x + 4 = 0 ⇔ x = -2. Løsningen fortæller, at f(x) rører eller skærer x-aksen i x = -2.

2. Man bruger ti-Nspire kommandoen: y=tangentLine(sqrt(2*x+4),x,0) ▸ y=x/2+2. Dvs. tangenten gennem punktet med førstekoordinaten 0 er:

   y = 0,5x + 2

3. Arealet er integralet fra 1 til 3 af f(x) og beregnes ved hjælp af Ti-Nspire kommandoen:

   

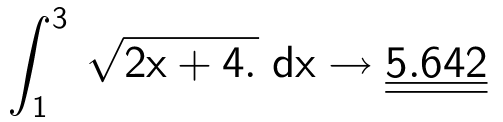
Svar på opgave 9:

1. Der er tale om positiv lineær vækst. x er antal år efter 1999, f(x) er samlet BT i mio.

   f(x) = 0,33·x + 2,46 mio.

2. Man finder året ved først at beregne antal år efter 1999 i Ti-Nspire:

   solve(0.33*x+2.46=5,x) → x = 7.697

   Årstallet bliver: 1999 + 7 = 2006

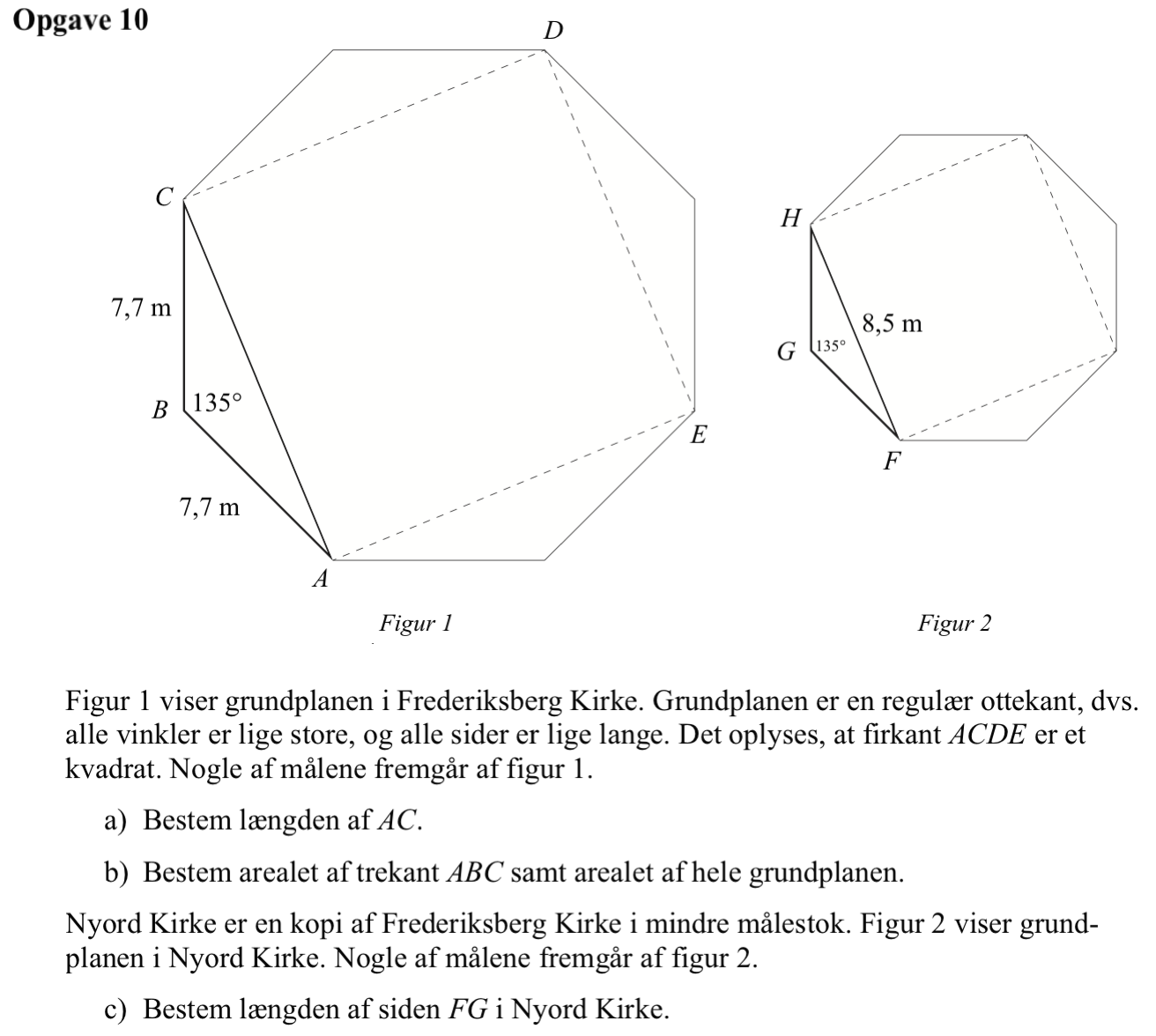
Svar på opgave 10:

1. Trekant ABC er en ligebenet trekant med benlængden 7,7 m og topvinklen 135°. Grundlinjen er |AC|. Vinkel A er (180° - 135°)/2 = 22,5°. Man får:

   |AC| = 2·7,7m·cos(22,5°) = 14,23 m

2. Arealet af trekant ABC er ½·højde·14,23 m. Højden er 7,7 m·sin(22,5°) = 2,947 m.

   Arealet af ABC er derfor: ½·2,947 m·14,23 m = 20,97 m²

   Arealet af hele grundplanen er 4·20,97 m² + 14,23 m·14,23 m = 286,4 m²

   Konrol-løsning i Geogebra:

   

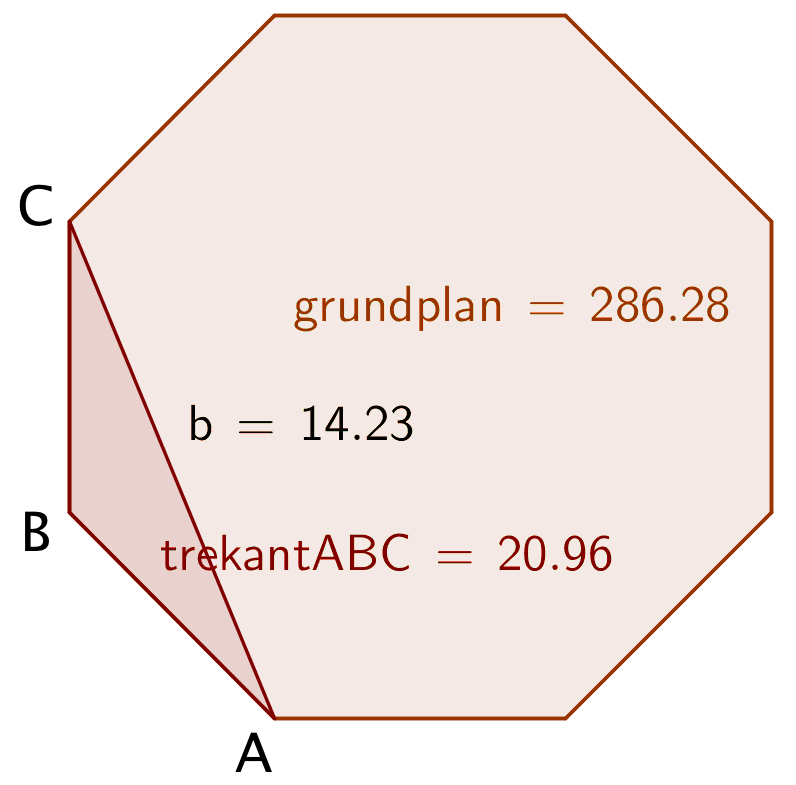
3. Sidelængden = |FG|. Trekant ABC og trekant FGH er ensvinklede.

   Der gælder |FG|/7,7m = 8,5m/14,23m ⇒ |FG| = 7,7 m·(8,5 m/14,23 m) = 4,60 m

Svar på opgave 11:

1. Fedtprocenten er 42,9·ln(28) 102,7 = 40,3

2. F = 42,9·ln(BMI) - 102,7 ⇒

   F + 102,7 = 42,9·ln(BMI) ⇒

   (F + 102,7)/42,9 = ln(BMI) ⇒

   BMI = exp[(F + 102,7)/42,9]

Svar på opgave 12:

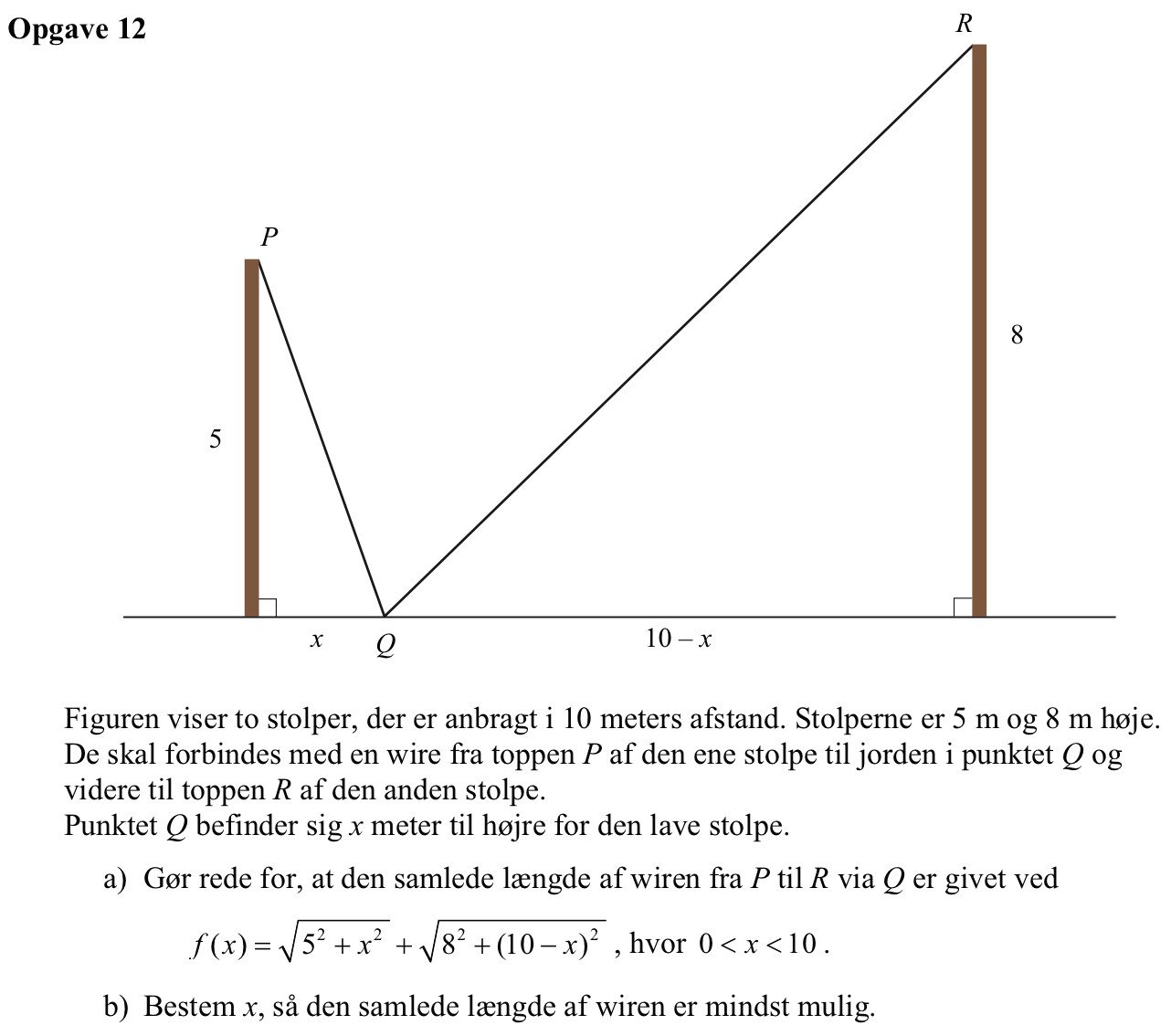
1. Stolperne og wiren danner to retvinklede trekanter, hvor |PQ| og |QR| er hypotenuserne. Wirens længde er |PQ| + |QR|.

   Der gælder: |PQ|² = 5² + x² og |QR|² = 8² + (10 - x)²

   Wirens længde er derfor: √[5² + x²] + √[8² + (10 - x)²]

   (x skal være mellem 0 og 10, da x skal ligge mellem stolperne)

2. For at finde mindstepunktet bestemmer man nulpunkterne for f´(x) og undersøger fortegn for f´(x) omkring dem. Man får:

   solve(derivative(sqrt(5²+x²)+sqrt(8.²+(10-x)²),x)=0,x) ▸ x=3.84615

   Fortegnene for f´(x) undersøges for x = 3 og x = 4:

   derivative(sqrt(5²+x²)+sqrt((8.)²+(10-x)²),x)|x=3 ▸ −0.144009 (wirens længde er aftagende)

   derivative(sqrt(5²+x²)+sqrt((8.)²+(10-x)²),x)|x=4 ▸ 0.024695 (wirens længde er voksende)

   Dette viser, at det x, der giver den mindste længde af wiren, er x = 3,846 m

   (I Ti-Nspire kan man også finde værdien af x med kommandoen fMin(): fMin(sqrt(5²+x²)+sqrt(8.²+(10-x)²),x) ▸ x=3.846)