
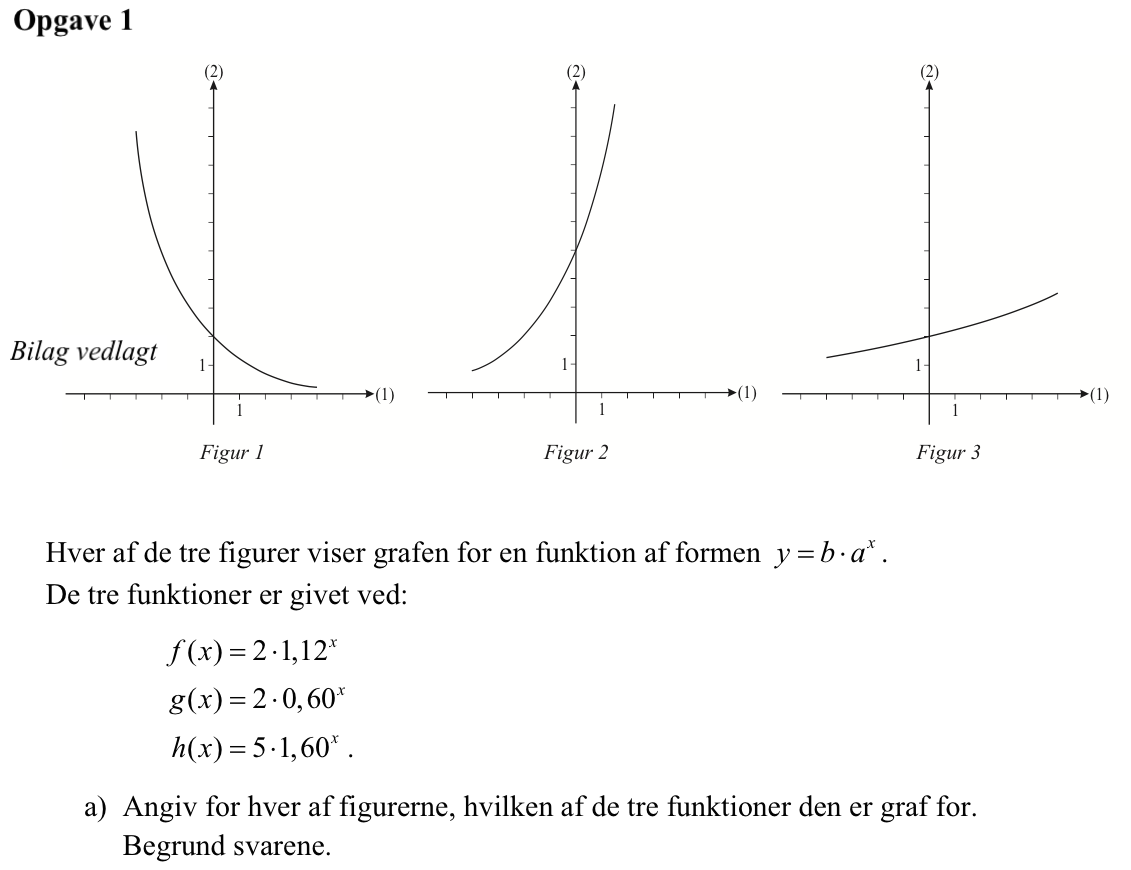
Svar på opgave 1:
-
Figur 1 viser en aftagende (0 < a < 1) eksponentialfunktion, som skærer y-aksen i y = 2 (b = 2). Dette svarer til g(x)
Figur 2 viser en voksende (a > 1) eksponentialfunktion, som skærer y-aksen i y = 5 (b = 5). Dette svarer til h(x)
Figur 2 viser en voksende (a > 1) eksponentialfunktion, som skærer y-aksen i y = 2 (b = 2). Den vokser langsommere end funktionen i figur 2, og a for funktion i figur 3 er derfor mindre end a for funktionen i figur 2. Dette svarer til f(x)
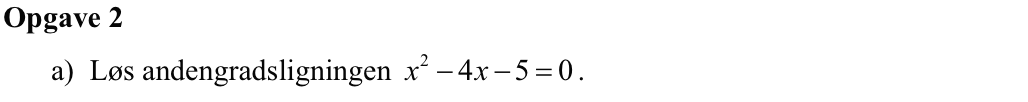
Svar på opgave 2:
-
x2 - 4x - 5 = 0 ⇔
x = 2 ± ½·√(16 + 4·5) ⇔
x = 2 ± ½·√(36) ⇔
x = 2 ± ½·6 ⇔
x = 2 ± 3 ⇔
x = -1 ∨ x = 5

Svar på opgave 3:
-
Der er tale om en voksende lineær funktion. Tallet 17,4 fortæller hvor meget antallet af Playstations vokser med i millioner stk. om året. Tallet 10,6 fortæller hvor mange millioner Playstations, der var i år 2001.
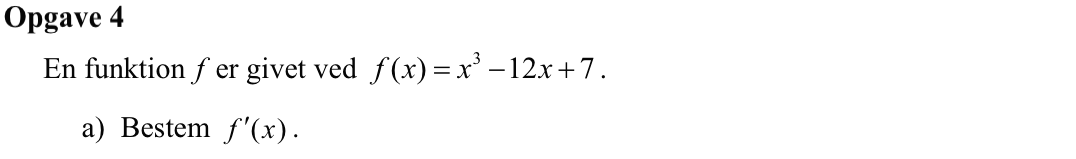
Svar på opgave 4:
-
f´(x) = 3x2 - 12
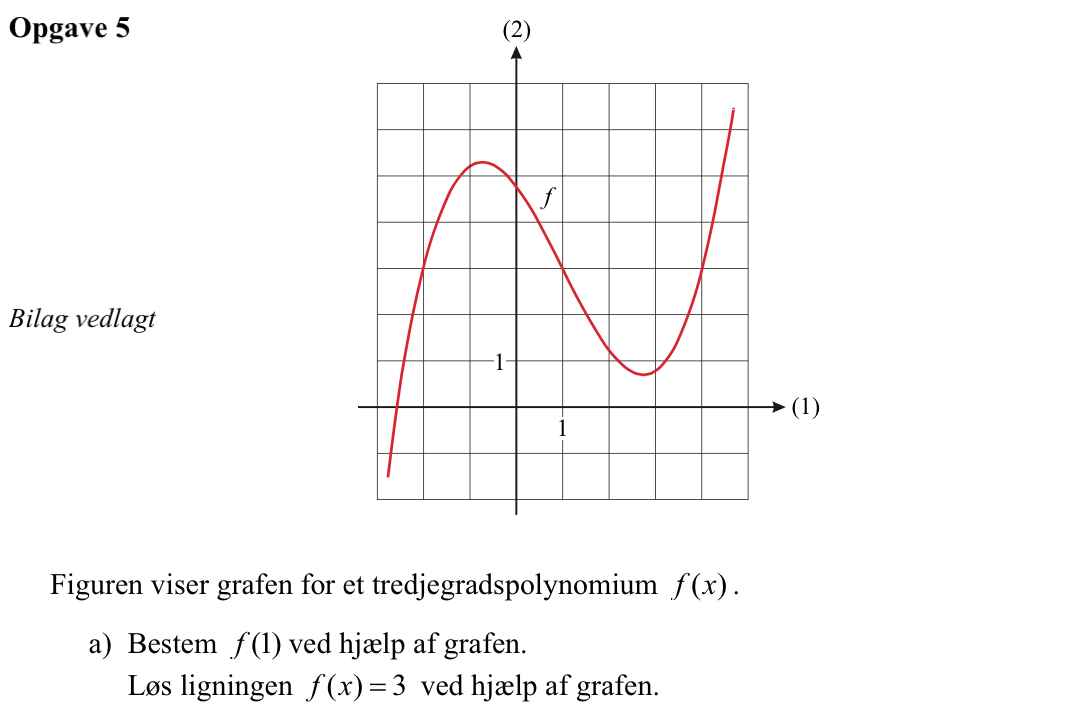
Svar på opgave 5:
-
f(1) er lig med 3. Dette aflæses på tegningen som vist:
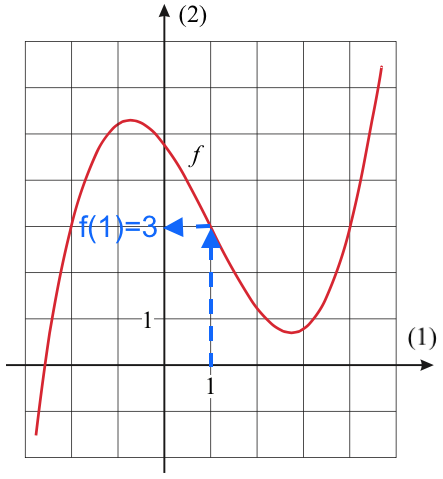
-
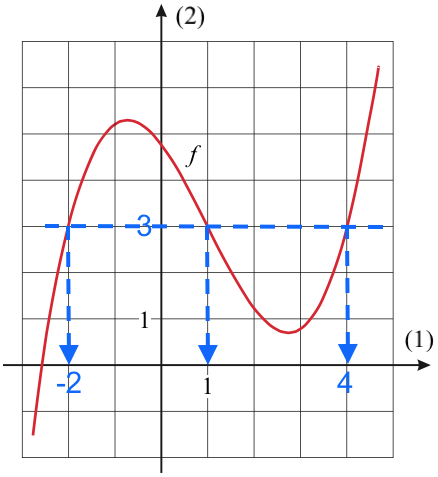
Løsningen til ligningen f(x) = 3 aflæses til x = -2 ∨ x = 1 ∨ x = 4.
Dette er vist på tegningen som x-værdierne til skæringspunkterne mellem grafen til f og den vandrette linje y = 3:
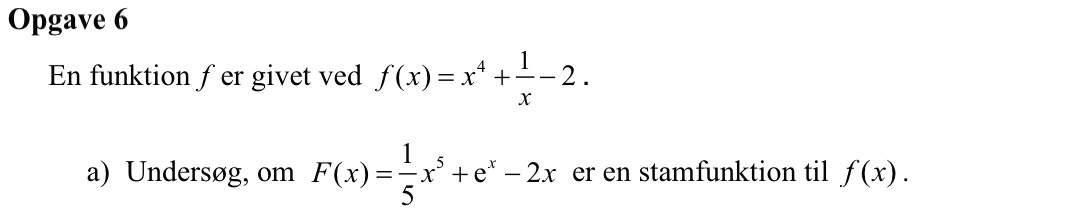
Svar på opgave 6:
-
Man skal undersøge om F(x) differentieret er lig med f(x). Man får:
F(x)' = x4 + ex - 2, som er forskellig fra f(x). Dermed er F(x) ikke stamfunktion til f(x).



Svar på opgave 7:
-
Man opretter to lister i Ti-Nspire: en for antallet af år efter 2001 og en for antallet af industrirobotter:
listeår:={2001,2002,2003,2004,2005,2006,2007,2008}-2001 ▸ {0,1,2,3,4,5,6,7}
listeantal:={2093,2342,2630,2926,3258,3626,4115,4622} ▸ {2093,2342,2630,2926,3258,3626,4115,4622}
Man foretager en eksponentiel regressionsanalyse i Ti-Nspire ved hjælp af kommandoen Statistik ▸ Statistiske beregninger ▸ Eksponentiel regressionsanalyse... og vælger de to lister fra menuerne. Man får resultatet:
ExpReg listeår,listeantal,1: CopyVar stat.RegEqn,f1: stat.results ▸

Det giver at a = 1,119 og b = 2091
(Det bemærkes, at Ti-Nspire bruger a og b modsat opgaveteksten.)
-
Den årlige procentvise stigning eller vækstrate er a - 1 = 1,119 - 1 = 0,119 = 11,9 %
-
Man skal beregne antallet af robotter for x = 2010 - 2001 = 9 og x = 2011 - 2001 = 10. Man benytter f1(x)=2010,71·1,11887x, som blev oprettet automatisk af Ti-Nspire ved regessionsanalysen (bemærk: f1: stat.results ovenfor). Man får:
f1(2010-2001) ▸ 5745.196
f1(2011-2001) ▸ 6428.118
Det ses at det bergnede antal robotter i 2010 er 5745 og i 2011 er antallet 6428. Begge tal ligger over det faktiske og regressions formlen giver derfor et forventet tal som er for højt.

Svar på opgave 8:
-
Som kontrol betragtes grafen for f som her er tegnet i Geogebra.
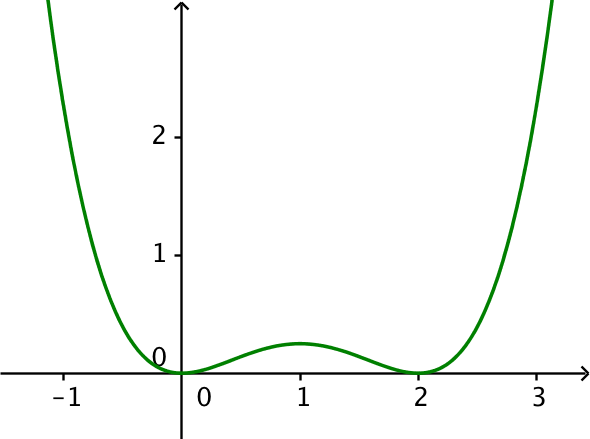
Det ser ud til at funktionen har to nulpunkter x = 0 og x = 2. Funktionen er aftagende før x = 0 og voksende eter x = 2. For x liggende mellem 0 og 2 er funktionen først voksende og derpå aftagende. Nulpunkterne for f er samtidig ekstremumspunkter.
Dette undersøges ved at finde nulpunkterne for både f og f'. Nulpunkterne for f findes i Ti-nspire:
f(x):=0.25*x4-x3+x2 ▸ Udført
solve(f(x)=0,x) ▸ x=0. or x=2.
solve(derivative(f(x),x)=0,x) ▸ x=0. or x=1. or x=2.
Dette viser at f(x) ganske rigtigt rører x-aksen for x = 0 og x = 2. Samtidig har f ekstremumspunkter for x = 0, x = 1 og x = 2.
Man udnersøger fortegn for f' omkring nulpunkterne: f'(-1) = -6, f'(0,5) = 0.375, f'(1,5) = -0.375, f'(3) = 6.
Dette viser at f aftager for x < 0, vokser for 0 < x < 1, aftager for 1 < x < 2 og vokser for x > 2. For x = 0 og x = 2 har f lokalt minimum og for x = 1 har f lokalt maksimum.
-
Tangenten til f gennem punktet (3,f(3)) findes i Ti-Nspire:
y=tangentLine(f(x),x,3) ▸ y=6*x-15.75
Dvs. tangentlinjen gennem (3,f(3)) har ligningen y = 6x - 15,75
-
Man skal finde arealet under kurven mellem x = 0 og x = 2. Dette beregnes i Ti-Nspire som integralet af f(x) mellem x = 0 og x = 2:
Integral(f(x),x,0,2) ▸ 0.2667
Arealet er 0,2667

Svar på opgave 9:
-
Man skal løse ligningen 1,7 = 1,24·x0,05. Det gøres i Ti-Nspire:
solve(1.7=1.24*x0.05,x) ▸ x=550.23
Dvs. bølgelængden er 550 m ved en bølgehastighed på 1,7 m/s
-
Der er tale om en potensfunktion, hvor a = 0,05 og man skal bruge formlen for procent-procentvækst. Man får:
Bølgelængden vokser med (1,250,05 - 1)·100% = 1,12 %
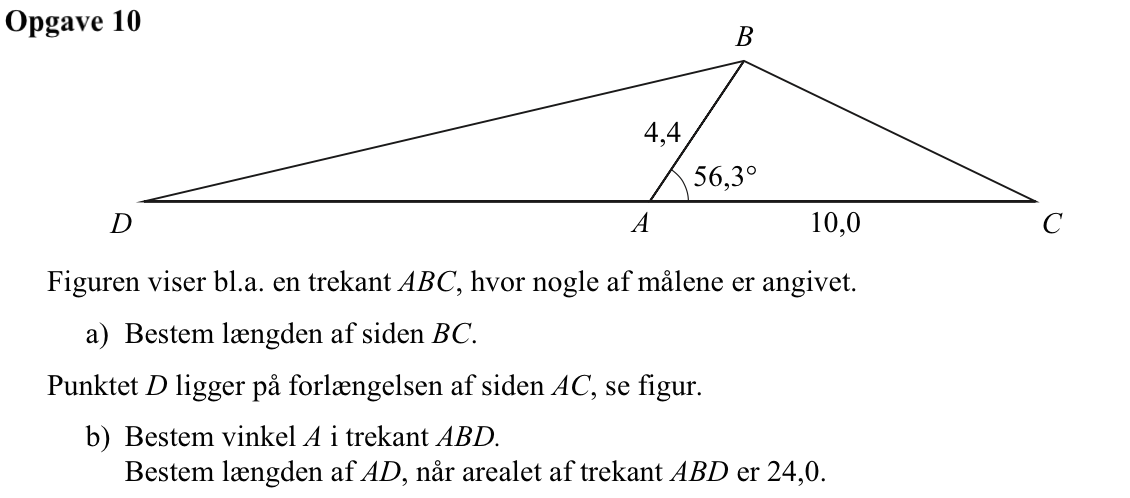
Svar på opgave 10:
-
Man finder |BC| ved hjælp af en cosinusrelation i Ti-Nspire, hvor x står for |BC|..
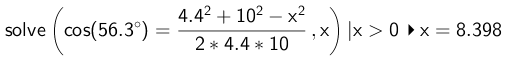
Dvs. |BC| = 8,40
-
Arealet af trekant ABD er ½·hB·|AD|, hvor hB er højden fra forlængelsen af AD til punktet B. hB kan findes som 4,4·sin(56,3°) = 3,661. Dette giver med hensyn til |AD|:
½·3,661·|AD| = 24 ⇒ |AD| = 24/(½·3,661) ⇒ |AD| = 13,1

Svar på opgave 11:
-
Højde (cm): 172 176 196
Armlængde (cm): 64 65 70
-
Sammenhængden er positiv lineær. Positiv fordi armlængden vokser, når højden vokser og lineær fordi, at man hver gang, der lægges et bestemt tal til højden, skal lægge et konstant tal til armlængden.
Formlen er y = ax + b, hvor y er armlængden a er forøgelsen af armlængden i cm, når højden forøges 1 cm, og b er armlængde for en person med højde 0. Dvs. a = 1/4 og b = 0. Man får y = (1/4)·x

Svar på opgave 12:
-
Man starter med at oprette f(x) i Ti-Nspire:
f(x):=800*(1/x)+70.9*sqrt(x) ▸ Udført
Man skal beregne f(10), dvs. indsætte x = 10 i formlen for forbruget af metalplade. Dette gøres i Ti-Nspire:
f(10) ▸ 304.21
Der skal derfor bruges 304,21 cm2 metalplade til en dåse med højden 10 cm.
-
Man beregner den højde (den værdi af x), der giver det mindste forbrug af stålplade (den mindste værdi af f(x)), ved hjælp af fMin()-kommandoen i Ti-Nspire:
fMin(f(x),x) ▸ x=7.98575
Dvs. den højde, der giver det mindste forbrug af metalplade er 7,99 cm