Svar på opgave 1:

1. f(x) = ax + b. Konstanten a er linjens hældning, som findes ud fra P og Q:

   a = (10 - 1)/(4 - 1) = 3. Dette giver:

   f(x) = 3x + b. Man finder b ved at indsætte P i formlen:

   f(1) = 1 ⇒ 1 = 3·1 + b ⇒ b = -2. Man har dermed f(x):

   f(x) = 3x - 2

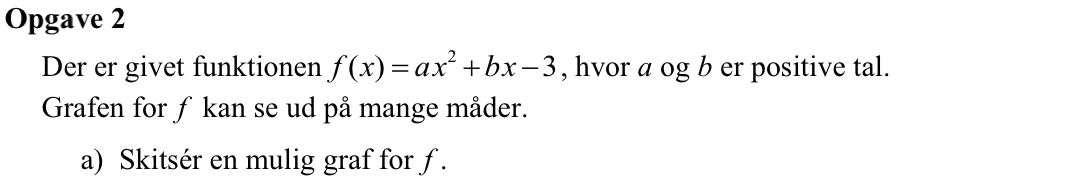
Svar på opgave 2:

1. Grafen går gennem punktet (0,c) = (0,-3). Da a > 0 vender grafens (eller parablens) grene opad, og da b > 0 er grafens hældning i punktet (0,-3) positiv. Det giver f.eks. nedenstående graf:

   

Svar på opgave 3:

1. f´(x) = 8x³ - 3

   g´(x) = 4/x

Svar på opgave 4:

1. Formlen kan skrives : f(x) = 150·1,39^x,

   hvor f(x) er antallet af markmus, x er antallet af måneder siden de slap ud, 150 er antallet af markmus fra starten og 1,39 er fremskrivningsfaktoren, som er 1 + vækstraten på 39 %.

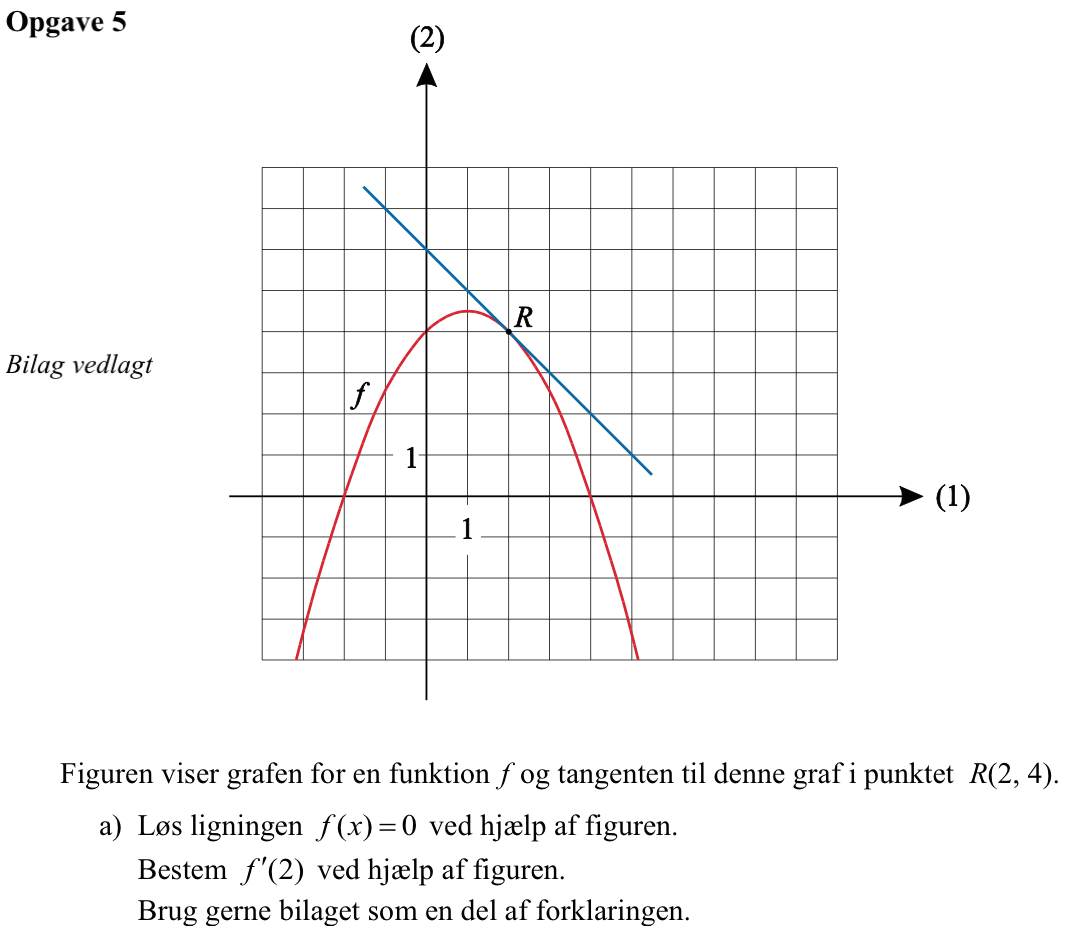
Svar på opgave 5:

1. Løsning af ligningen f(x) = 0 med hensyn til x giver x-værdierne for skæringspunkterne mellem grafen for f og x-aksen.

   Disse værdier aflæses til x = -2 ∨ x = 4

   f'(2) er hældningen til grafen i punktet (2,f(2)). Den blå linje er tangenten til grafen i dette punkt og kan derfor bruges til at finde f´(2).

   Det ses, at den blå linje går en enhed ned på y-aksen hver gang, man går en enhed frem på x-aksen. Dermed er hældningen i punktet -1 og man får, at

   f(2) = -1

Svar på opgave 6:

1. Samtlige stamfunktioner er

   

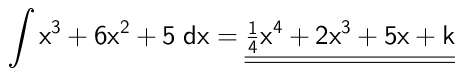
   hvor k er en vilkårlig konstant.

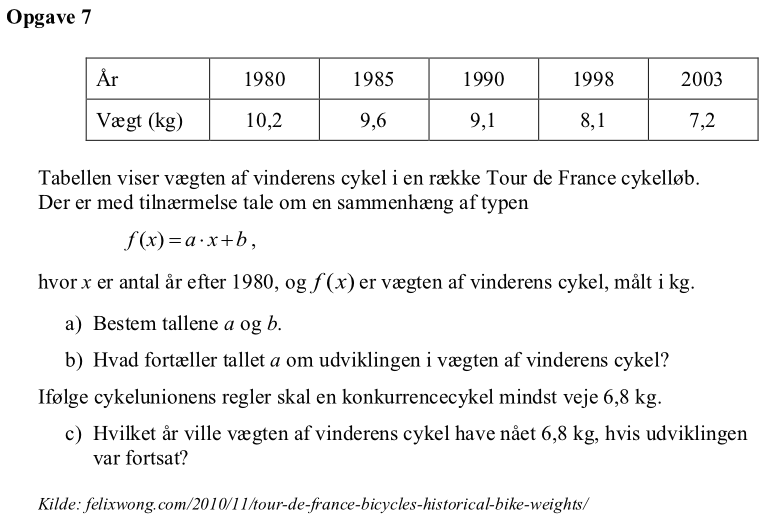
Svar på opgave 7:

1. Løsning i Geogebra. Man laver en potens-regressionsanalyse og får følgende kurve:

   listeår:={1980,1985,1990,1998,2003}-1980 ▸ {0,5,10,18,23}

   listevægt:={10.2,9.6,9.1,8.1,7.2} ▸ {10.2,9.6,9.1,8.1,7.2}

   

   Det giver: a = "m" = -0,1273 og b = 10,27

2. Koefficienten a viser, hvor meget vægten aftager med pr år. (Vægten aftager, fordi koefficienten er negativ.)

   Koefficienten b viser hvad vægten er til at starte med, dvs. når x = 0, der her svarer til året 1980.

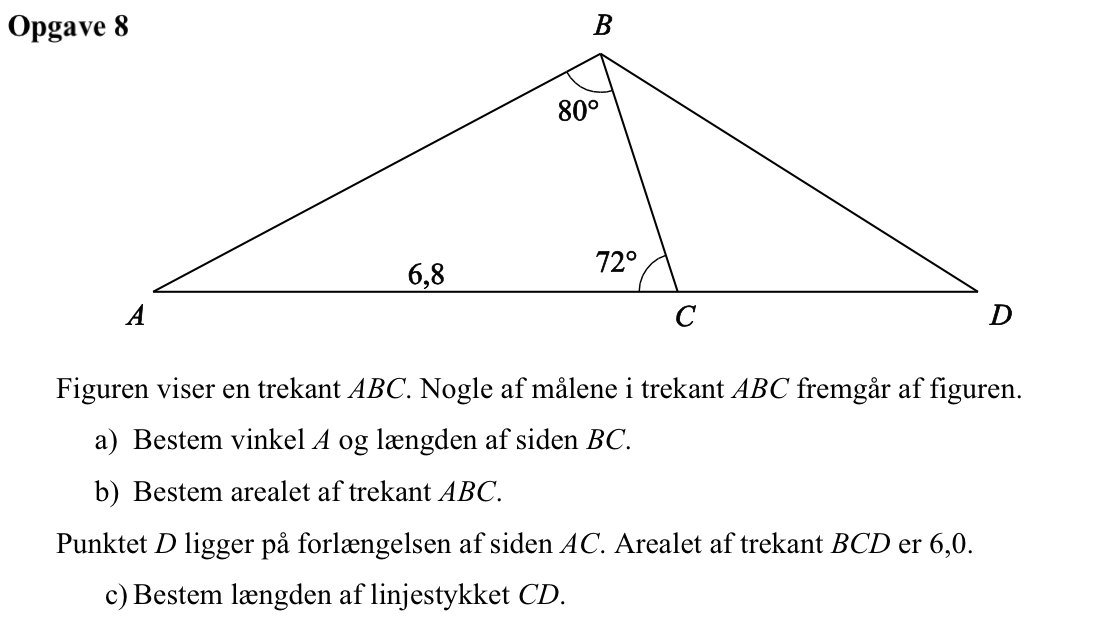
Svar på opgave 8:

1. Vinklen A findes ved hjælp af reglen om at vinkelsummen i en trekant er 180°. Man får: vinkel A = 180° - (80° + 72°) = 28°

   |BC| findes ved hjælp af en sinusrelation i Ti-Nspire (ac = siden AC, a = vinkel A og b = vinkel B):

   solve(bc/sin(a)=ac/(sin(b),bc)|a=28° and b=80° and ac=6.8 ▸ bc=3.242

   Dvs. |BC| = 3,242

2. Arealet er 0,5·højde·grundlinje = 0,5·h_B·|AC| = 0,5·3,242·sin(72°)·6,8 = 0,5·3,083·6,8 = 10,48

3. Arealet er 0,5·højde·grundlinje = 0,5·h_B·|CD| = 0,5·3,083·|CD|.

   Man ska løse ligningen 0,5·3,083·|CD| = 6,0 med hensyn til |CD| og får: solve(0.5*3.083*x=6,x) ▸ x=3.892

   Dvs. |CD| = 3,892

Svar på opgave 9:

1. Rumfanget er 37,5·4^2 cm³ = 600 cm³

2. Formlen for rumfanget er en potensfunktion hvor a = 2. Dobbelt så stort rumfang betyder en tilvækst af rumfanget vokser med 100 %. Man finder den procentvise tilvækst i radius ved at oprette V(r) i Ti-Nspire og bruge formlen for procent-procentvækst og solve-kommandoen til at finde r:

   v(r):=37.5*r² ▸ Udført

   solve(x²-1=1.,x)|x>0 ▸ x=1.4142 (x står for fremskrivningsfaktoren, dvs. 1 + den procentvise tilvækst som decimaltal.)

   Dvs. radius vokser med 1,4142 - 1 = 0,414 = 41,4 %

Svar på opgave 10:

1. f(x):=x³-1.5*x+3 ▸ Udført

   Man finder nulpunkterne for f´(x) i Ti-Nspire:

   solve(derivative(f(x),x)=0,x) ▸ x=−0.7071 or x=0.7071

   Man undersøger fortegnene for f´(x) omkring nulpunkterne:

   derivative(f(x),x)|x=−1 ▸ 1.5

   derivative(f(x),x)|x=0 ▸ -1.5

   derivative(f(x),x)|x=1 ▸ 1.5

   Undersøgelsen viser, at f vokser for x < -0,7071, aftager for -0,7071 < x < 0,7071 og

   vokser igen for x > 0,7071

2. Man finder ligningen til tangenten gennem (1,f(1)) ved hjælp af følgende komando i Ti-Nspire:

   y=tangentLine(f(x),x,1) ▸ y=1.5*x+1.

   Dvs. tangentens ligning er y = 1,5x + 1

3. Man finder de x, hvor f´´(x) = 1,5 ved hjælp af solve-kommandoen i Ti-Nspire:

   solve(derivative(f(x),x)=1.5,x) ▸ x=−1. or x=1.

   Det ses at f´(x) = 1,5 for x = −1 ∨ x = 1. For disse x-værdier har f hældningen 1,5.

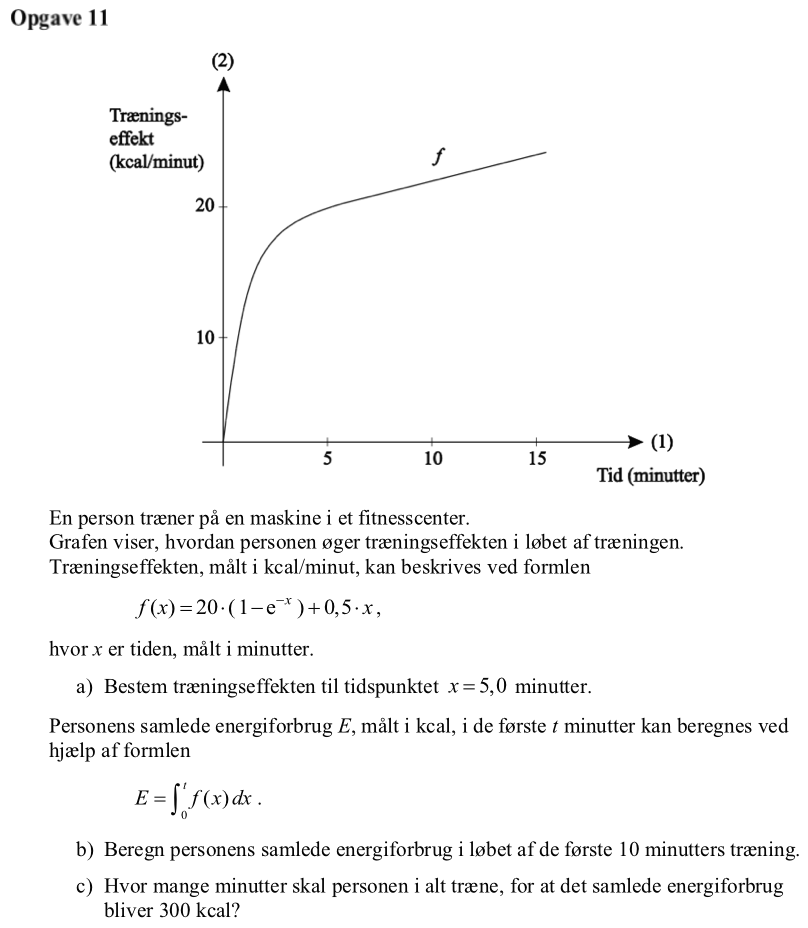
Svar på opgave 11:

1. Man skal finde f(5) som gøres i Ti-Nspire:

   f(x):=20*(1-exp(−x))+0.5*x ▸ Udført

   f(5) ▸ 22.3652

   Dvs. f(5) = 22,37 kcal./min.

2. Man opretter E(t) i Ti-Nspire og finder E(10):

   e(t):=Integral(f(x),x,0,t) ▸ Udført

   e(10) ▸ 205.001

   Dvs. det samlede energiforbrug i løbet af de første 10 minutter er 205,0 kcal.

3. Man bruger solvekommandoen til at ligningen E(t) = 300 med hensyn til t:

   solve(e(t)=300,t)|t>0 ▸ t=13.665

   Dvs. der går 13,7 minutter eller 13 minutter og 40 sekunder før det samlede

   energiforbrug er 300 kcal.