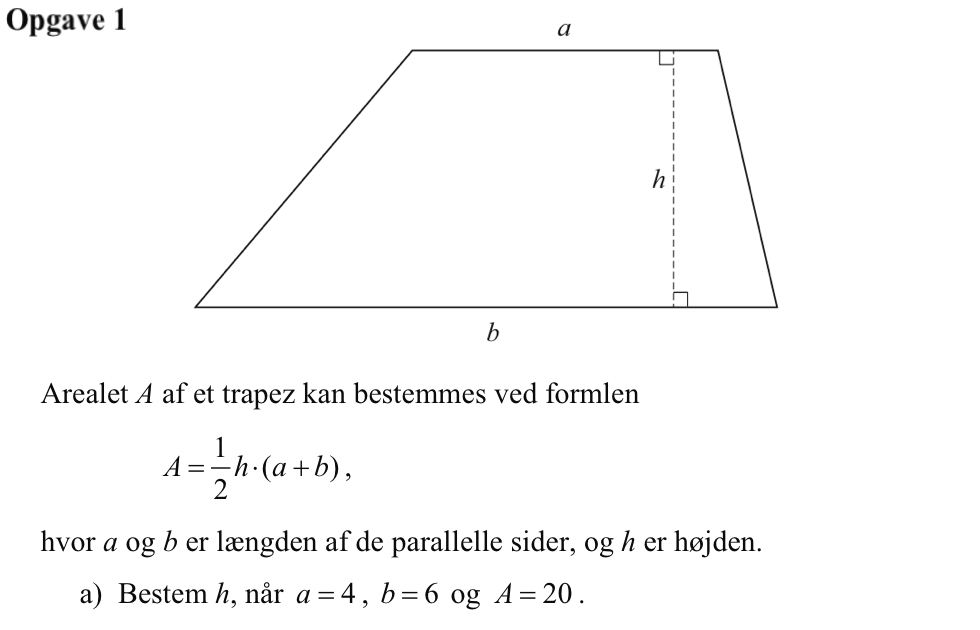
Svar på opgave 1:

1. Man skal isolere h i formlen for arealet:

   A = 0,5·h·(a + b) ⇒ h = A/[0,5·(a + b)]

   Det giver h = 20/[0,5·(4 + 6)] = 20/[0,5·10] = 20/5 = 4

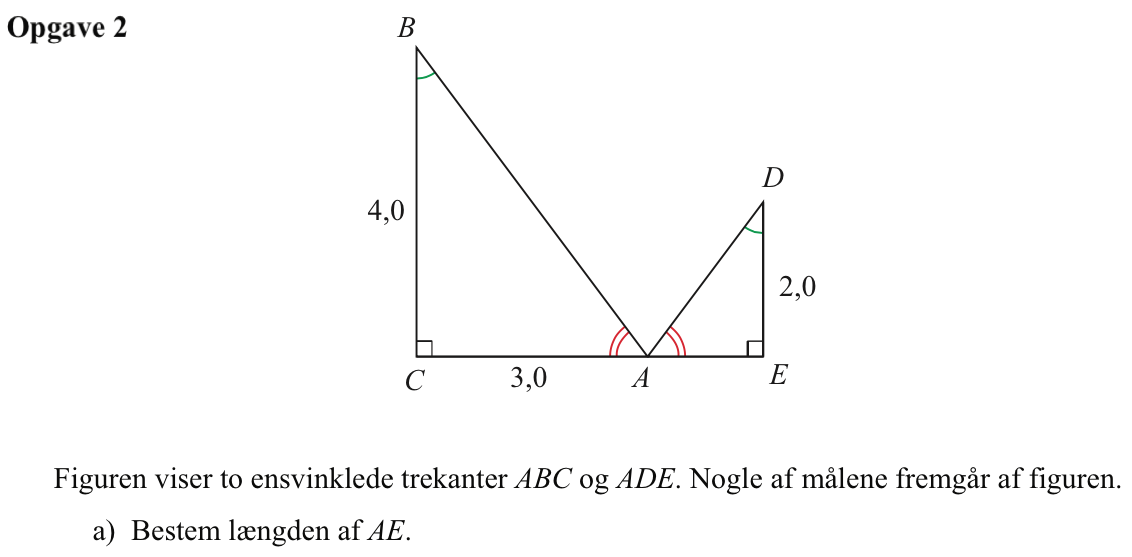
Svar på opgave 2:

1. De to ensvinklede trekanter har skaleringsfaktoren |BC|/|DE| = 4/2 = 2. Der gælder |CA|/|AE| = 2 ⇒ 3/|AE| = 2 ⇒ |AE| = 3/2 = 1,5

Svar på opgave 3:

1. Man skal finde forskriften for den lineære funktion (eller linjens lignng) for at se om punktet (30,19) opfylder forskriften.

   Der gælder, at f(x) = ax + b, hvor a og b er reelle tal. Man finder a ud fra de kendte punkter (0,5) og (4,7): a = (7-5)/(4-0) = 0,5

   Dette giver f(x) = 0,5x + b. Koefficiente b findes ved at indsætte (0,5) i forskriften: f(x) = 0,5·0 + b = 5 ⇒ b = 5. Det giver den færdige forskrift: f(x) = 0,5x + 5.

   Man indsætter (x,f(x)) = (30,19) i forskiften for at se om højre og venstre side af lighedstegnet giver det samme:

   Venstre: 19; højre: 0,5·30 + 5 = 20. Dvs. punktet (30,19) ligger ikke på grafen for f

Svar på opgave 4:

1. Denne parabel, som er tegnet i Geogebra opfylder betingelserne:

   

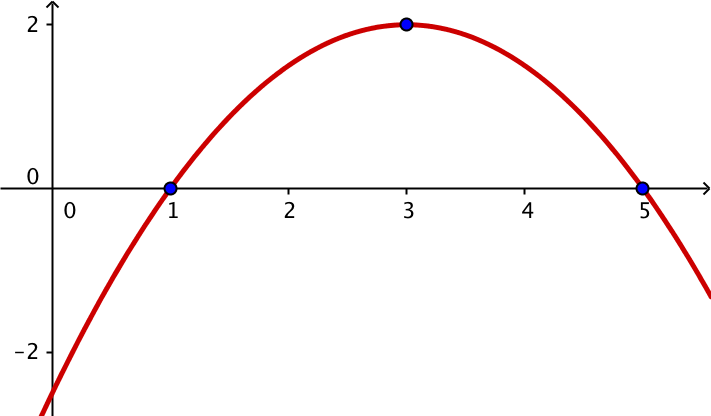
   a < 0 fordi grenene vender nedad, b > 0, fordi hældningen ved parabelens skæring med y-aksen er positiv og c < 0 fordi parablen skærer y-aksen's negative halvdel.

Svar på opgave 5:

1. Man bruger modellen f(x) = 5,56·1,29^x,

   hvor f(x) er antallet af mennesker i millioner, x er antal år efter 2011, 5,56 er antal millioner mennsker i 2011 og 1,29 er fremskrivningsfaktoren = 1 + 29%.

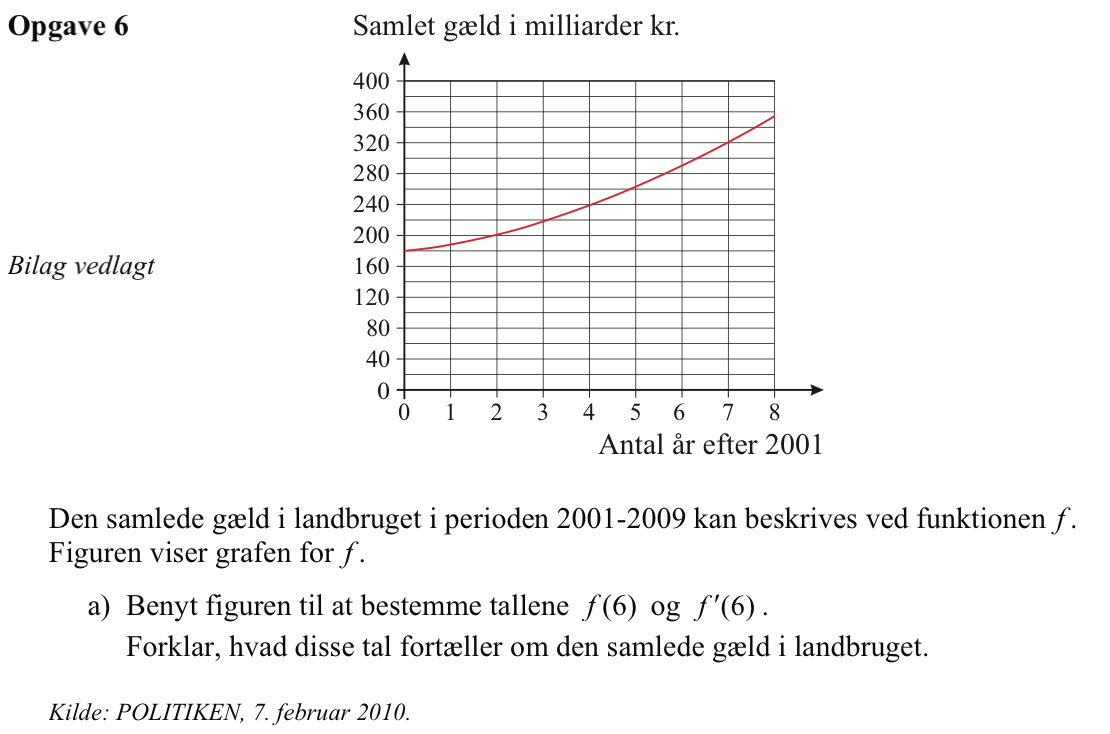
Svar på opgave 6:

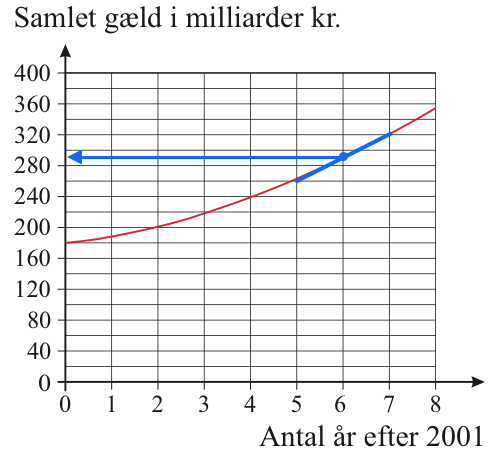
1. f(6) aflæses som vist til 290 mia. kr.

   f´(6) beregnes som hældningen af den skrå blå linje: f´(6) = 40 mia./2 år = 20 mia./år

   

Svar på opgave 7:

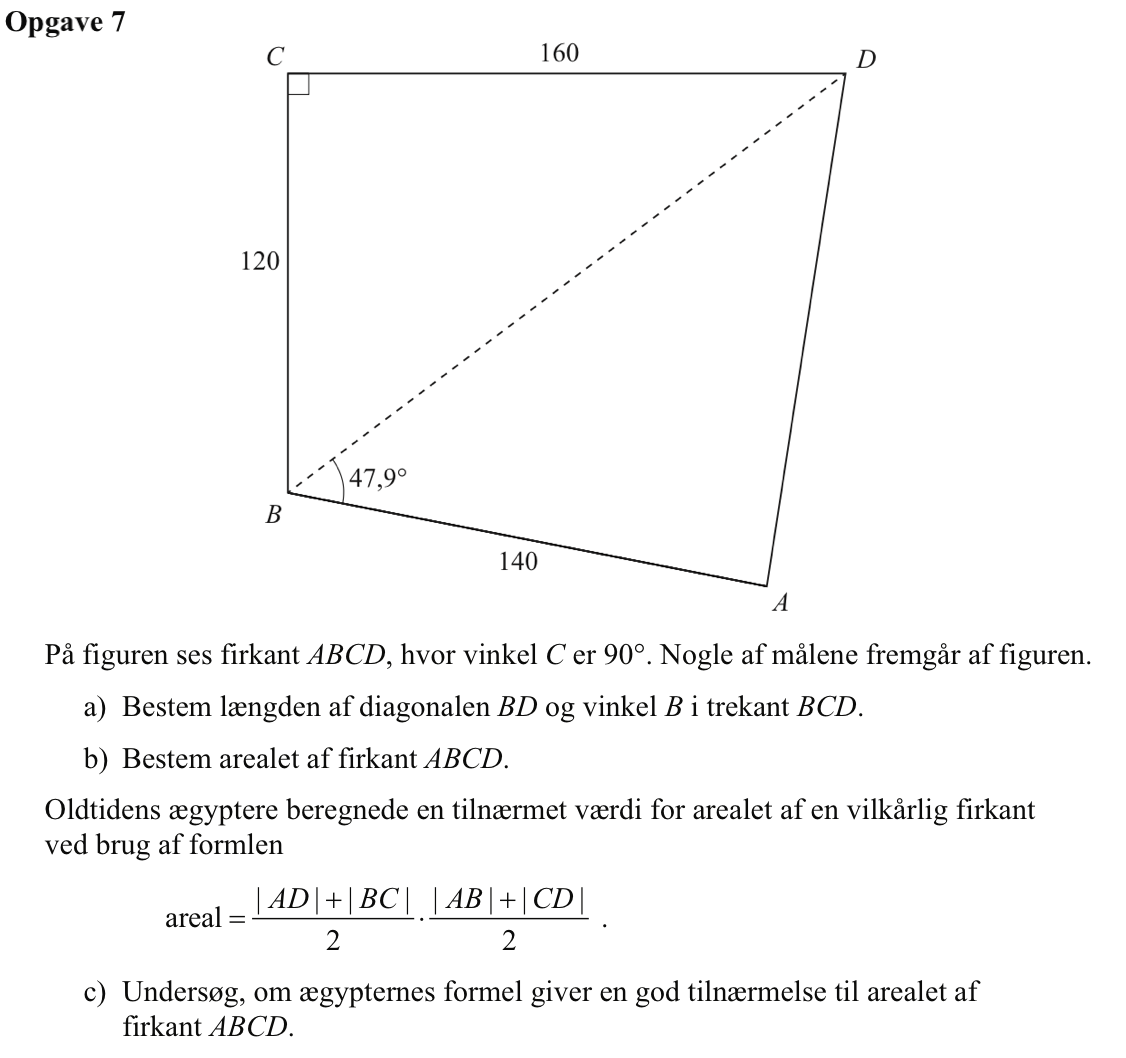
1. BD er hypotenusen i en retvinklet trekant. Dens længde findes ved hjælp af Pythagoras læresætning: |BD| = √(120² + 160²) = 200

   Der gælder om vinkel B i trekant BCD, at |BD|·sin(∠B) = 160 ⇒ 200·sin(∠CBD) = 160 ⇒ ∠B = sin^-1(160/200) ⇒ ∠B = 53,13°

2. Arealet af trekant BCD er 0,5·120·160 = 9600

   Arealet af trekant ABD er 0,5·|BD|·h_A = 0,5·200·|CA|·sin(∠ABD) = 0,5·200·140·sin(47,9°) = 10387.66

   Arealet af firkant ABCD er summen af de to trekanters areal: 9600 + 10388 = 19988

3. Man finder først |AD| ved hjælp af en cosinusrelation i Ti-Nspire:

   solve(cos(47.9°)=(200²+140²-ad²)/(2*200*140),ad)|ad>0 ▸ ad=148.51

   Dette indsættes sammen med de kendte sidelængder i den ægyptiske formel:

   (148,5 + 120)·(140 + 200)/(2·2) = 22822,5. Som det ses giver den ægyptiske formel et tal, der er for højt og er ikke nogen god tilnærmelse.

Svar på opgave 8:

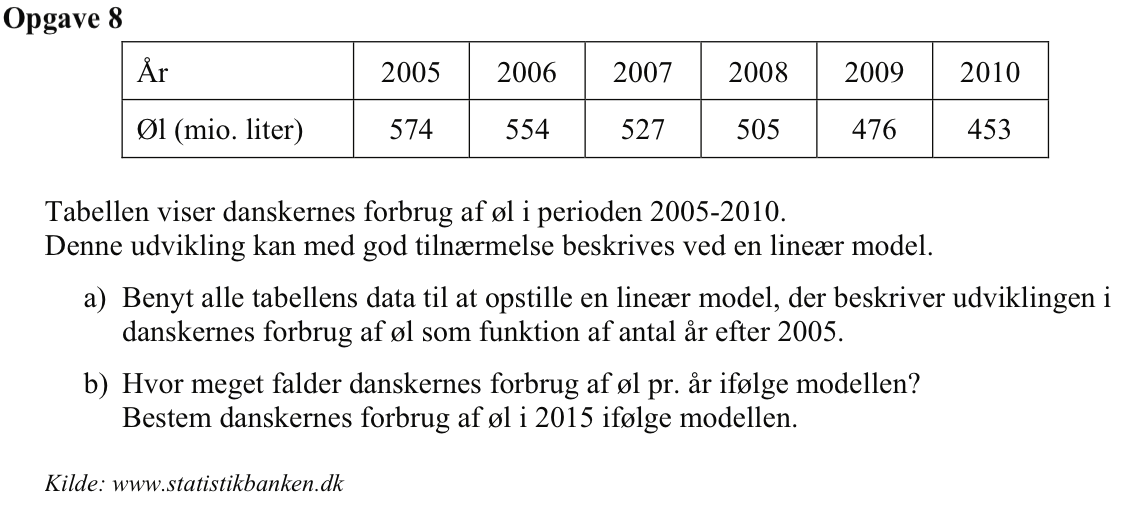
1. Man opretter lister med antallet af år efter 2005 og antal mio. liter øl som lister i Ti-Nspire:

   listeår:={2005,2006,2007,2008,2009,2010}-2005 ▸ {0,1,2,3,4,5}

   listeøl:={574,554,527,505,476,453} ▸ {574,554,527,505,476,453}

   Man bruger kommandoen Statistik ▸ Statistiske beregninger ▸ Lineær regression (mx+b)... og får:

   

   Dvs. den lineære model bliver: f(x) = -24,6x + 576,3,

   hvor f(x) antal mio. liter øl drukket på et år og x er antal år efter 2005.

2. I følge modellen falder danksernes forbrug med 24,6 mio. liter om året. I følge modellen var forbruget i 2005 på 576,3 mio. liter

Svar på opgave 9:

1. Man finder en vilkårlig stamfunktion F(x) til f(x) ved at finde det ubestemte integrale af f(x):

   F(x) = 2·¼·x⁴ + 6·⅓·x³ - 4x = ½x⁴ + 2x³ - 4x + k, hvor k er en tilfældig konstant.

2. Man skal finde det k, der gør, at F(2) = 10. Man får: ½·2⁴ + 2·2³ - 4·2 + k = 10 ⇒ ½·16 + 2·8 - 4·2 + k = 10 ⇒ 8 + 16 - 8 + k = 10 ⇒ k = -6. Den søgte stamfunktion er dermed:

   F(x) = ½x⁴ + 2x³ - 4x - 6

Svar på opgave 10:

1. Man skal finde f(30) = 69,5·30^0,76 kcal/døgn = 921,7 kcal/døgn

2. f(x) er en potensfunktion, og man skal bruge formlen for procent-procent vækst for f(x), når x vokser med 100 % (eller når fremskrivningsfaktoren er 2).

   Man får, at stofskiftet er (2^0,76 - 1)·100 % = 69,4 % større for hanbavianer end for hunbavianer.

Svar på opgave 11:

1. Grafen for f er tegnet nedenunder i Geogebra.

   

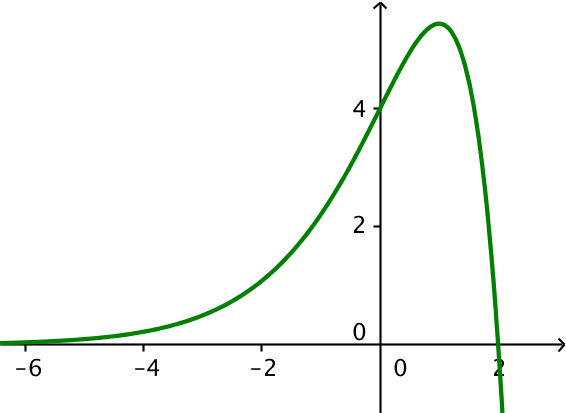
   Skæringen mellem grafen for f og x-aksen er løsnngen til ligningen f(x) = 0 med hensyn til x. Man får følgende i Ti-Nspire:

   solve(f(x)=0,x) ▸ x=2

   Dvs. grafen for f skærer x-aksen for x = 2

2. Arealet af området er integralet af f(x) fra x = 0 til x = 2. Man får følgende i Ti-Nspire:

   integral(f(x),x,0,2.) ▸ 8.778

   Dvs. arealet af området i første kvadrant er 8,778

3. Ligningen f´(x) = 0 løses i Ti-Nspire:

   solve(derivative(f(x),x)=0,x) ▸ 1.

   Dvs. f´(x) = 0 for x = 1

   Det ses af grafen, at f hat maksimum for x = 1. Maksimummet er f(1) = (4-2·1)·e¹ = 2·e = 5,437

Svar på opgave 12:

1. Man skal beregne h(2) = 200 - 6,0·2 + 27,5·(e^-1,6·2 - 1) m = 161,6 m

2. Man skal løse ligningen h(t) = 0 med hensyn til t. Man får følgende i Ti-Nspire:

   solve(h(t)=0,t) ▸ t=28.75

   Dermed rammer faldskærmsudspringeren jorden efter 28,8 s

3. Man skal beregne h´(2). Det gøres i Ti-Nspire med kommandoen:

   derivative(h(t),t)|t=2 ▸ −7.7935

   Dvs. faldhastigheden er 7,794 m/s

   (Minustegnet betyder, at retningen er nedad og kan kan udelades, da man ved, at det er et fald.)