Svar på opgave 1:

1. Nedenstående figur viser grafen for f(x) = x² - (10/3)·x.

   

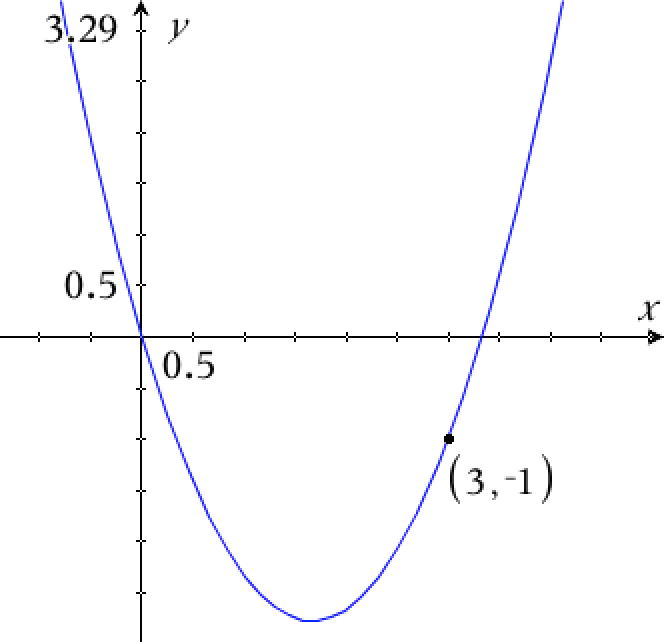
   At a er positiv betyder, at grenene på parablen vender opad. Diskriminanten (for den den tilsvarende andengradsligning) er positiv, da parablen har to skæringspunkter med x-aksen.

Svar på opgave 2:

1. Formlen er f(x) = 220 - (2/3)·x, hvor f(x) er maksimumspulsen og x er alderen i år.

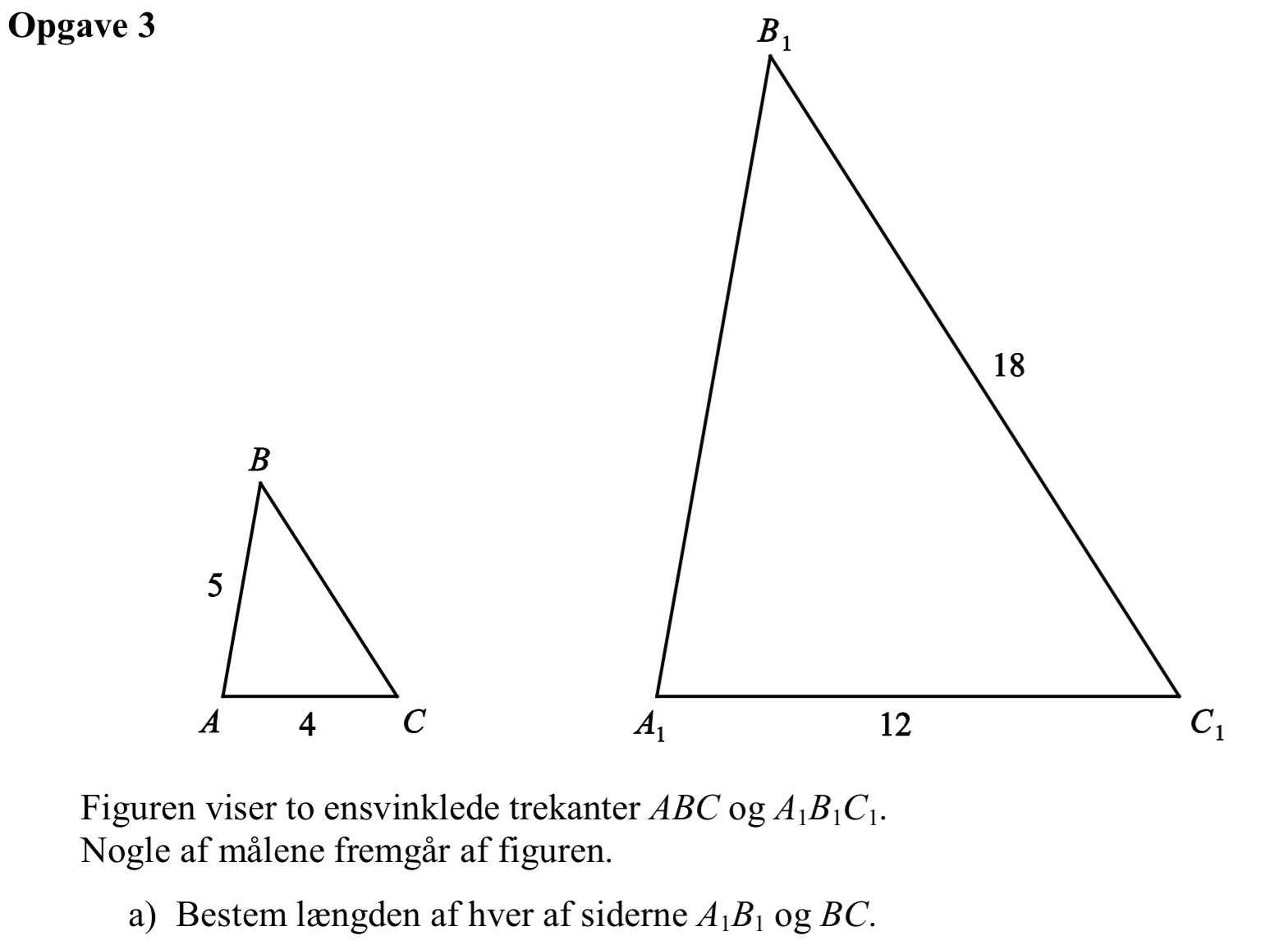
Svar på opgave 3:

1. Skaleringsfaktoren for de to trekanter er 12/4 = 3.

   |A₁B₁| = 5·3 = 15

   |BC| = 18/3 = 6

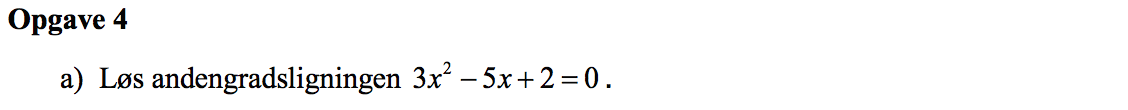
Svar på opgave 4:

1. 3x² - 5x + 2 = 0 ⇔

   x = 5/(2·3) ±(1/(2·3))·√[25 - 4·3·2] ⇔

   x = 5/6 ± (1/6)·√[1] ⇔

   x = 5/6 ± 1/6 ⇔

   x = 5/6 - 1/6 ∨ x = 5/6 + 1/6 ⇔

   x = 2/3 ∨ x = 1

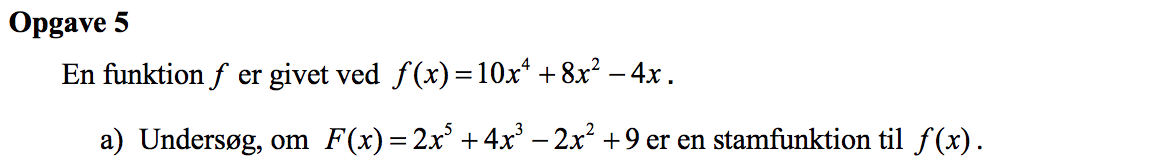
Svar på opgave 5:

1. Man skal undersøge om F'(x) er lig med f(x). Man får:

   F'(x) = 10x⁴ + 12x² - 4x

   Da 10x⁴ + 12x² - 4x ikke er lig med forskriften for f er F ikke en stamfunktion til f.

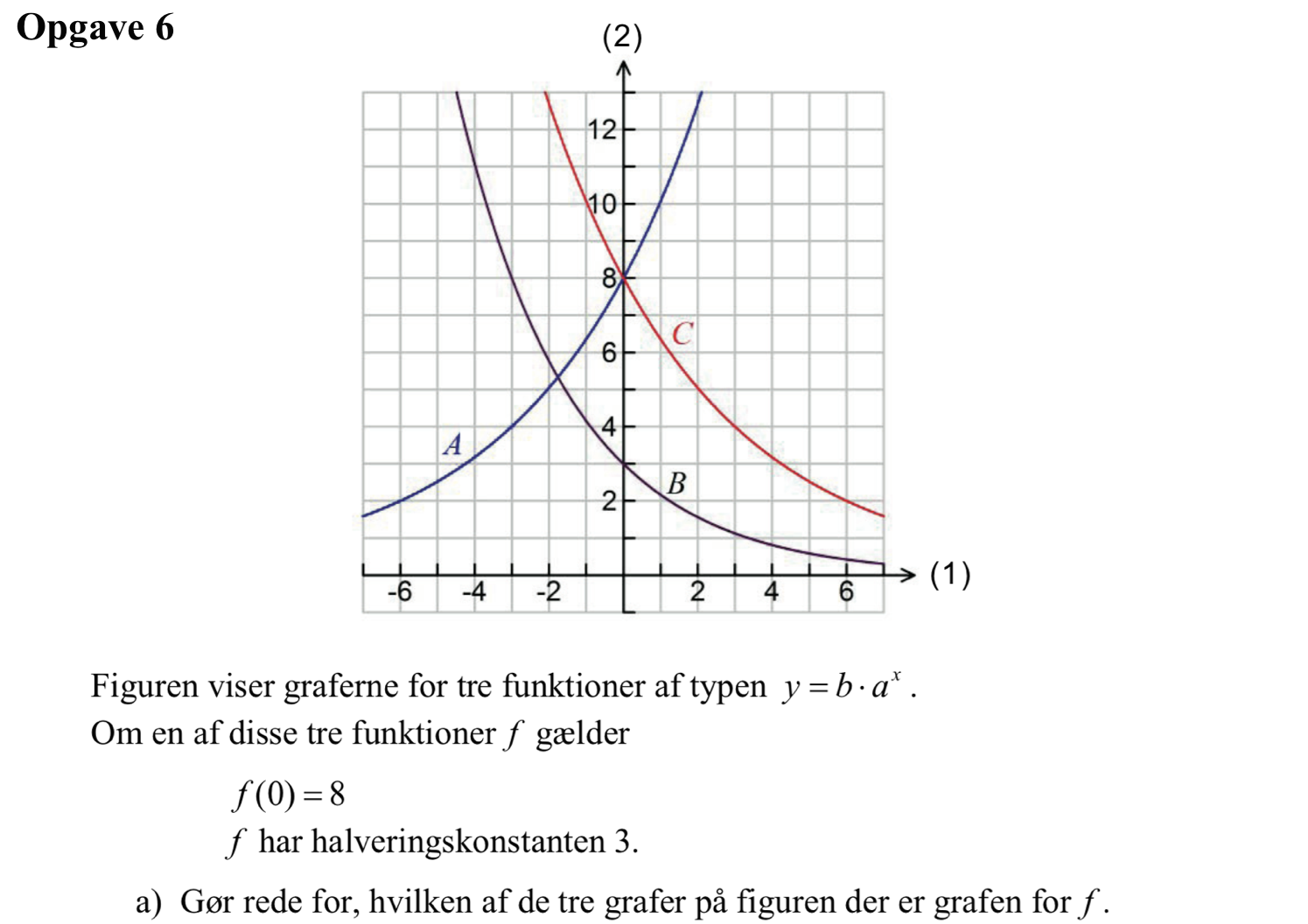
Svar på opgave 6:

1. Grafen C er den rigtige. Den går gennem (0,8), og når man bevæger sig 3 frem (f.eks. fra x = 0 til x = 3) halveres funktionsværdien.

Svar på opgave 7:

1. Man opretter f(x) i Ti-Nspire:

   f(x):=5.5*(0.932)^x ▸ Udført

   Man beregner befolkningen i år 1550:

   f(1550-1531) ▸ 1.443

   Dvs. der var 1,44 mio. mennesker i 1550

2. Tallet 5,5 er startværdien i mio., dvs. befolkningstallet for x = 0 eller i år 1531.

   Tallet 0,932 er fremskrivningsfaktoren, dvs. det tal, som man skal gange det gamle års befolkningstal med for at få det nye.

3. Man skal løse ligningen f(x) = 2,75 med hensyn til x. Man får:

   solve(f(x)=2.75,x) ▸ x=9.8427

   Dvs. befolkningen når ned på 2,75 mio. i år 1531 + 9,8 = 1541

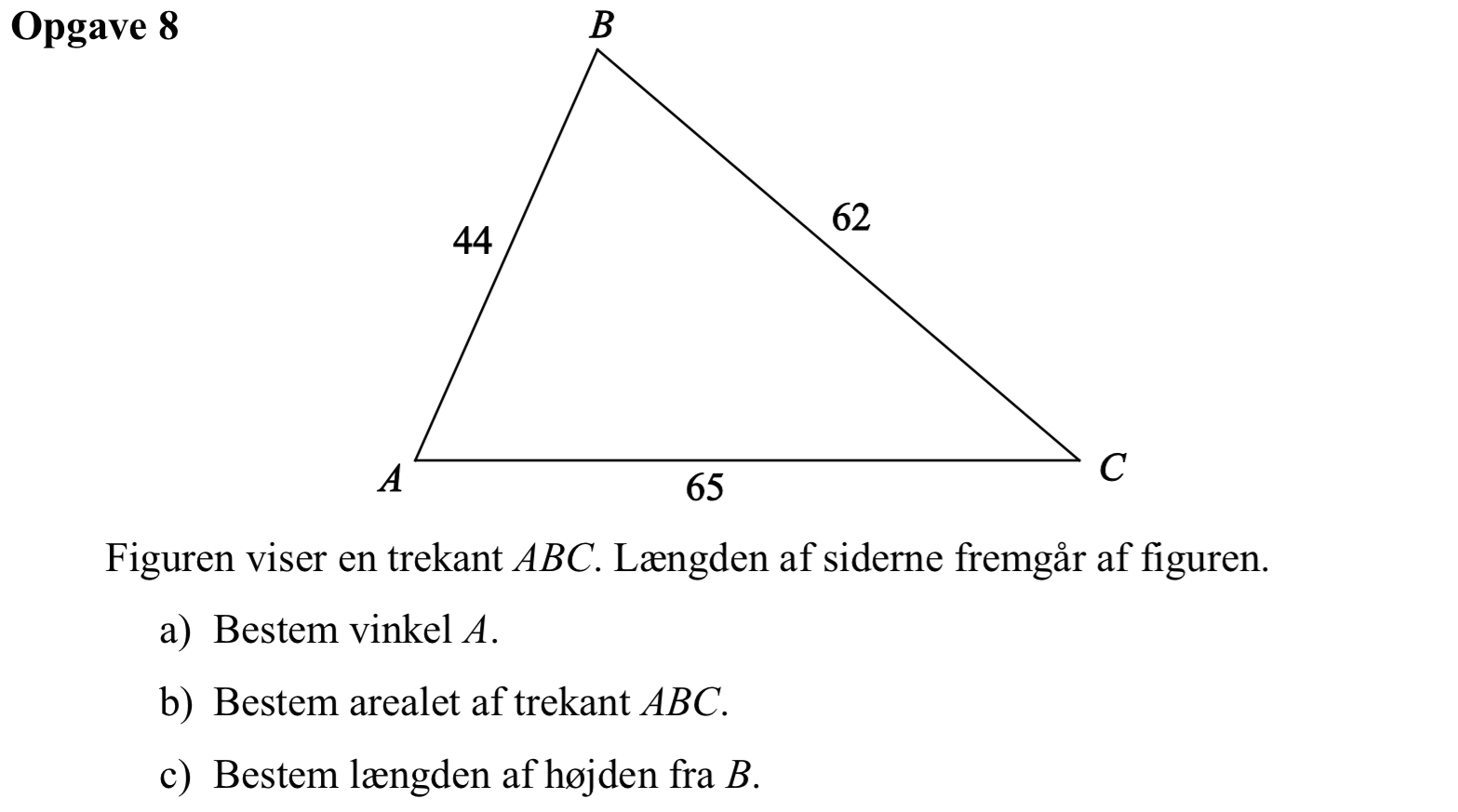
Svar på opgave 8:

1. Man benytter en cosinusrelation til at finde vinkel A i Ti-Nspire:

   solve(cos(x*1.°)=((44²+65²-62²)/(2*44*65)),x)|0<x<180 ▸ x=66.1045

   Dvs. vinkel A er 66,1°

2. Nedenstående tegning viser trekant ABC med højden i B indtegnet.

   

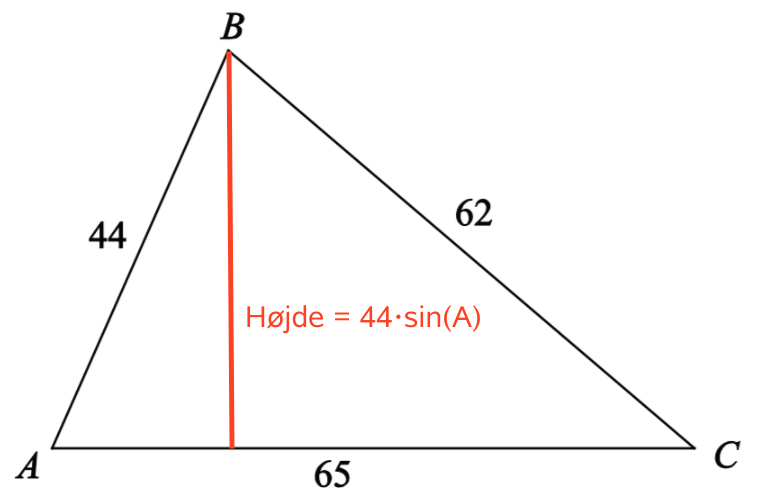
   Arealet er en halv højde gange grundlinje = 0,5·44·sin(66,1°)·65 = 1307,4

3. Højden i B er 44·sin(∠A) = 44·sin(66,1°) = 40,2

Svar på opgave 9:

1. Man opretter en liste med antal brikker i Ti-Nspire:

   antal_brikker:={22,48,67,80,100,154,240} ▸ {22,48,67,80,100,154,240}

   tid:={137,391,625,787,1251,2211,4024} ▸ {137,391,625,787,1251,2211,4024}

   Man laver potensregression på de to lister i Ti-NSpire med kommandoen Beregninger ▸ Stattistik ▸ Statistiske beregninger ▸ Potensregrssion...

   PowerReg antal_brikker,tid,1: CopyVar stat.RegEqn,f1: stat.results ▸
   [["Titel","Potensregression"]
   ["RegEqn","a*x^b"]
   ["a",1.56425]
   ["b",1.43441]
   ["r²",0.997944]
   ["r",0.998971]
   ["Resid","{...}"]
   ["ResidTrans","{...}"]]

   Man udskriver regressionsfunktionen f1(x), der er oprettet af Ti-Nspire:

   f1(x) ▸ 1.56425*x^1.43441

   Dvs. a = 1,434 og b = 1,564

2. Man skal løse ligningen f(x) = 3000 med hensyn til x i Ti-Nspire:

   solve(f1(x)=3000,x) ▸ x=194.366

   Dvs. man kan samle 194 brikker på 3000 sekunder

3. Man bruger formlen for procent-procent vækst for potensfunktioner når r = 100 %:

   (1 + 100 %)^1.434 = 2^1.434 = 2,70195

   Dvs. det tager 2,7 gange så lang tid at samle A som det tager at samle B.

Svar på opgave 10:

1. Man opretter f(x) i Ti-Nspire:

   f(x):=2*x-exp(x)+3 ▸ Udført

   Man bestemmer den aflede funktion:

   derivative(f(x),x) ▸ 2-exp(x)

   Dvs. f´(x) = 2 - e^x

2. Man bruger kommandoen tangentLine i Ti-Nspire. Man kan som her sætte "y=" foran kommandoen for at få hele ligningen på en gang:

   y=tangentLine(f(x),x,0) ▸ y=x+2

   Dvs. tangenten er y = x + 2

3. Man skal løse ulighederne f´(x) < 0 og f´(x) > 0. Dette gøres i Ti-Nspire:

   solve(derivative(f(x),x)<0.,x) ▸ x>0.693147

   solve(derivative(f(x),x)>0.,x) ▸ x<0.693147

   Dvs. f vokser for x < 0,693 og aftager for x > 0,693

   Det f vokser når x er mindre end 0,693 og aftager, når x er større har f globalt maksimumx i x = 0,693. Dette x indsættes i f(x):

   f(0.693) ▸ 2.3863

   Dvs. maksimumsværdien af f er 2,386

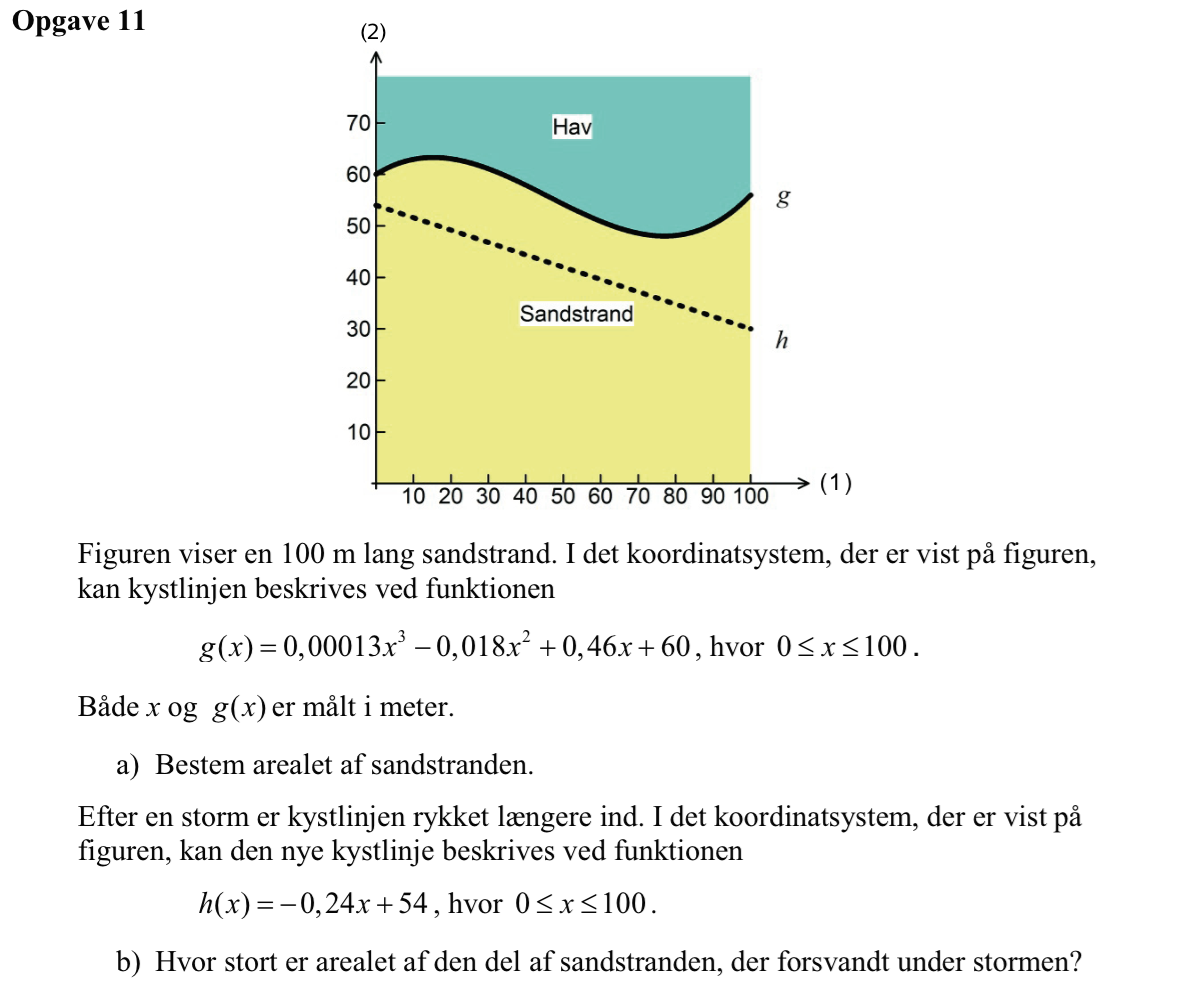
Svar på opgave 11:

1. Man opretter g(x) i Ti-Nspire:

   g(x):=1.3E−4*x³-0.018*x²+0.46*x+60 ▸ Udført

   Sandstrandens areal er integralet af g(x) fra x = 0 til x = 100. Man får følgende i Ti-Nspire:

   integral(g(x),x,0,100) ▸ 5550.

   Dvs. sandstrandens areal er 5550

2. Man opretter h(x) i Ti-Nspire:

   h(x):=−0.24*x+54 ▸ Udført

   Arealet af stykket, som er skyllet væk, er integralet af g(x) minus h(x) fra x = 0 til x = 100.

   integral(g(x)-h(x),x,0,100) ▸ 1350.

   Dvs. arealet af stykket, som er skyllet væk, er 1350