Svar på opgave 1:

1. 2(a - 8) + a + 20 = 2a - 16 + a + 20 = 3a + 4

   14x⁵/(7x²) = (14/7)·x^5-2 = 2x³

Svar på opgave 2:

1. Formlen er f(x) = 1200·(1+27%)^x = 1200·(1,27)^x,

   hvor f(x) er antallet af fugle og x er antal år efter 2005

Svar på opgave 3:

1. f´(x) = [x³ - 4x²]' = 3x² - 8x

Svar på opgave 4:

1. Påstand 1 og 2 er korrekte.

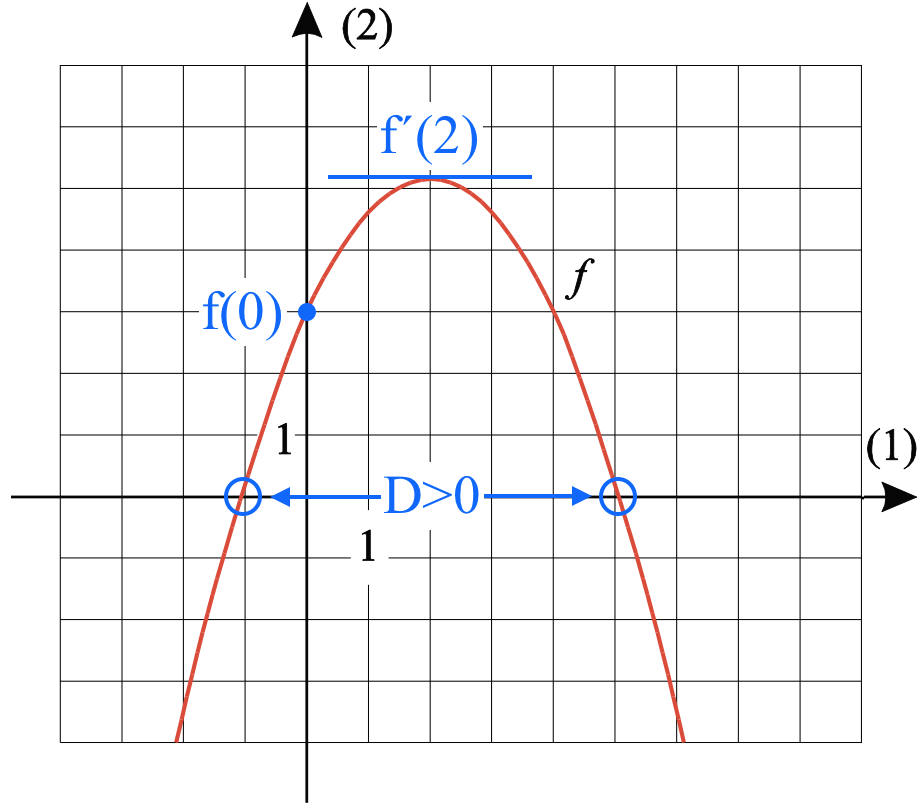
   3 er forkert, da f har to nulpunkter, og da diskriminanten dermed er positiv.

   På figuren nedenunder er vist med blåt, at f(0) = 3 (prik), at f´(2) = 0 (streg), og at der er to nulpunkter (ringe), hvilket gør at diskriminaten (D) er større end nul.

   

Svar på opgave 5:

1. Nedenunder er skemaet udfyldt.

   

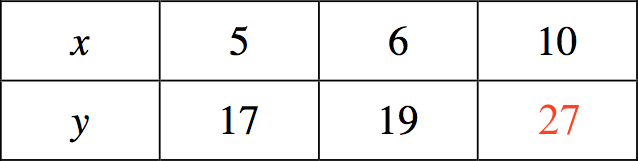
   Af de første to kolonner ses det, at y stiger med 2, når x stiger med 1. I den sidste kolonne er x steget med 4, og y skal dermed stige med 8 i forhold til 19. Dette giver sammenlagt 27.

Svar på opgave 6:

1. Man bruger integrationsreglerne for potensfunktioner og får: ∫8x³ dx = 2x⁴

Svar på opgave 7:

1. -4,64 viser, at produktionen aftager med 4,64 mia. m³ om året.

   217 viser, at produktionen af naturgas i 2008 er 217 mia. m³. (Året 2008 svarer til x = 0, og y(0) = -4,64·0 + 217 = 217.)

Svar på opgave 8:

1. Man opretter lister med antal år efter 2005 (antal_år) og antal studerende, der har gæld (gæld):

   antal_år:={2005,2006,2007,2008,2009,2010}-2005 ▸ {0,1,2,3,4,5}

   gæld:={43000,45900,48700,51600,54700,57800} ▸ {43000,45900,48700,51600,54700,57800}

   Man laver en eksponential regression på de to lister:

   ExpReg antal_år,gæld,1: CopyVar stat.RegEqn,f1: stat.results ▸
   [["Titel","Eksponentiel regression"]
   ["RegEqn","a*b^x"]
   ["a",43175.1]
   ["b",1.06071]
   ["r²",0.999348]
   ["r",0.999674]
   ["Resid","{...}"]
   ["ResidTrans","{...}"]]

   Heraf ses at a = 1,06071

   (Det bemærkes, at "a" fra opgaven kaldes "b" i CAS.)

2. Fordoblingstiden er ln(2)/ln(a) = ln(2)/ln(1,06071) år = 11,8 år

   Fordoblingstiden er det antal år, der går, for hver gang antallet af studerende med gæld fordobles.

Svar på opgave 9:

1. Trekant ACD er retvinklet og |AC| kan dermed findes ved hjælp af Pythagores læresætning.

   |AC|² = |AD|² + |CD|² ⇒

   |AC|² = 6,4² + 4,8² ⇔

   |AC|² = 64 ⇒

   |AC| = √64 = 8

   Dvs. længden af AC er 8 m

   Vinklen A findes ved hjælp af formlen: tan(∠A) = (modstående katete)/(hosliggende katete). Dette giver:

   solve(tan(a*1.°)=4.8/6.4,a)|0<a<90 ▸ a=36.8699

   Dvs. vinkel A = 36,9°

2. |AE| findes ved hjælp af en sinusrelation. Man skal til dette bruge vinklen AED, der findes ved hjælp af reglen om, at vinkelsummen i en trekant er 180°. Dette giver ∠AED = 180°-36.8699°-14° = 129,13°.

   solve(6.4/sin(129.13°)=ae/sin(14°),ae) ▸ ae=1.99597

   Dvs. |AE| = 2,00 m

3. Man skal finde arealet af trekant AED. Arealet af trekanten er 0,5·grundlinje·højde. Her er højden |AE|·sin(∠A) = 2,00·sin(36,87°) m = 1,2 m.

   Man får dermed, at arealet af det udækkede område er: 0,5·6,4·1,2 m² = 3,84 m²

Svar på opgave 10:

1. Det årlige antal bilulykker på en vej, hvor den tilladte hastighed er 80 km/t er: 0,0025·80² = 16

2. Man bruger formlen for procent-procent vækst for potensfunktioner: 1 + r_y = (1 + r_x)^a, hvor r_x er vækstprocenten for x, r_y er vækstprocenten for y og a er 2. Man skal finde r_y:

   r_y = ((1+(12,5%))²-1)·100 % = 26,56 %

   Dvs. antallet af peronskader vil stige med 16,6 %,

   hvis man øger hastigheden med 12,5 %.

Svar på opgave 11:

1. Man opretter funktionerne f(x) og g(x).

   f(x):=0.5*x^1.5 ▸ Udført

   g(x):=2*sqrt(x) ▸ Udført

   Man finder arealet ved at integrere funktionen (g(x) - f(x)) fra x = 1 til x = 3. Man får:

   integral(g(x)-f(x),x,1,3) ▸ 2.67718

   Dvs. arealet af området er 2,68

Svar på opgave 12:

1. Man opretter f(t):

   f(t):=−15*e^−0.12*t+20 ▸ Udført

   Man bestemmer f(5):

   f(5) ▸ 11.7678

   Dvs. sodavandens temperatur efter 5 minutter er 11,8 °C

2. Man skal finde f´(5):

   derivative(f(t),t)|t=5 ▸ 0.987861

   Dvs. efter 5 min. vokser sodavandens temperatur med 1,0 °C/min.

Svar på opgave 13:

1. Man opretter f(x).

   f(x):=x²-30*x+400+(500/x) ▸ Udført

   Man finder f(8): f(8.) ▸ 286.5, dvs. f(8) = 286,5

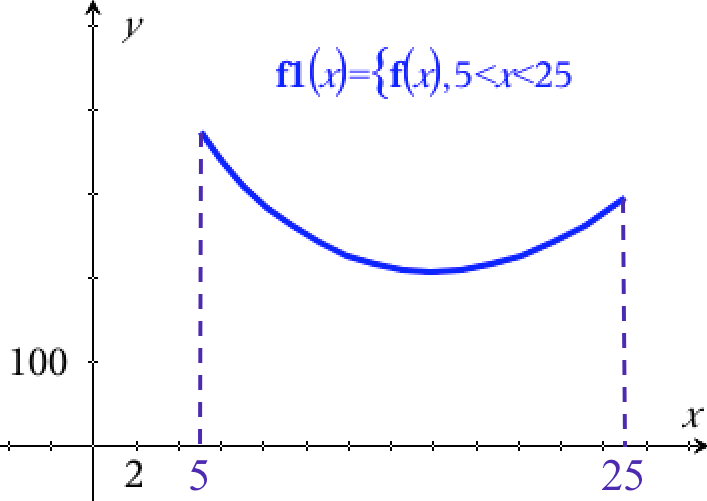
   Nedenunder er grafen for f(x) vist:

   

2. Man skal løse uligheden f(x) < 250.

   solve(f(x)<250.,x)|5<x<25 ▸ 10.<x<22.2474

   Dvs. produktionen skal være mellem 10 og 22,2 tons for, at prisen skal være under 250 kr./ton.

3. Minimumspunktet findes ved at undersøge f(x) i endepunkter og i punkter hvor f´(x) = 0. Man løser først f´(x) = 0:

   solve(derivative(f(x),x)=0,x) ▸ x=15.9791

   Endepunkterne er x = 5 og x = 25. Man får følgende værdier af f(x) i endepunkterne og x = 15,9791:

   f(5) ▸ 375

   f(25) ▸ 295

   f(15.9791) ▸ 207.25

   Dvs. det antal ton, der giver de lavste omkostninger pr. ton, er: 15,9791 ton = 16,0 ton