Svar på opgave 1:

1. Reducering:

   a³·a⁴·a^-1 = a^3+4-1 = a⁶

   x⁷/x² = x⁷·x^-2 = x^7-2 = x⁵

Svar på opgave 2:

1. P(100,193) ligger på grafen for f, hvis f(100) = 193. Man får:

   f(100) = 2·100 - 7 = 193, dvs. P ligger på grafen for f

Svar på opgave 3:

1. Modellen er: f(x) = 35·x + 40,

   hvor f(x) er vægten i gram og x er antal dage efter udklækningen.

Svar på opgave 4:

1. For grafen:...

   

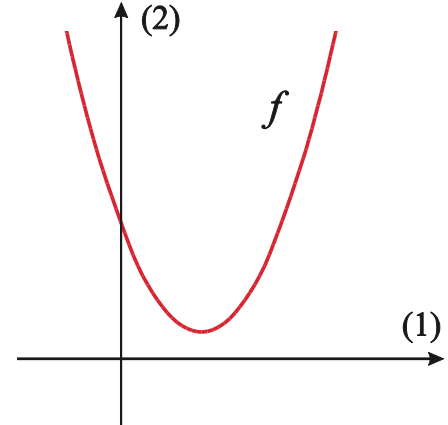
   gælder:...

   a > 0, da grafens grenene vender opad,

   b < 0, da grafens hældning i skæringen med y-aksen er negativ,

   c > 0, da grafens skæring med y-aksen er positiv og

   d < 0, da grafen ikke skærer x-aksen.

Svar på opgave 5:

1. Man bruger reglerne for integration af potensfunktioner: ∫4x³ + 10x - 3 dx = x⁴ + 5x² - 3x

Svar på opgave 6:

1. Tangenten til kurven gennem punktet (1,0) følger formlen: y = f'(1)·(x-1) + f(1) = f'(1)·(x-1).

   Her mangler man at bestemme f´(1).

   Man får at f´(x) = [x³ - x]' = 3x² - 1. Dermed er f´(1) = 3·1² - 1 = 2.

   Dette giver, at tangentens ligning er y = 2x - 2

Svar på opgave 7:

1. |BD| bestemmes ved hjælp af en cosinusrelation:

   solve(cos(46.1°)=(93²+87²-bd²)/(2*93*87),bd)|bd>0 ▸ bd=70.6921

   Dvs. |BD| = 70,7

2. Man finder vinkel ABD ved hjælp af en cosinusrelation:

   solve(cos(abd*1.°)=(93²+70.6921²-87²)/(2*93*70.6921),abd)|0<b<180 ▸ abd=62.4707

   Dvs. vinkel ABD = 62,5°

   Vinkel ADB findes ved hjælp af reglen om, at vinkelsummen i en trekant er 180°:

   Vinkel ADB = 180° - 62,4707° - 46,1° = 71,4°

3. |BC| findes ved hjælp af sinusrelationen sin(C)/|BD| = sin(BDC)/|BC|. Her er vinkel BDC = 180° - 71,4293° = 108,571°. Man får:

   solve(sin(31.1°)/70.6921=sin(108.571°)/bc,bc) ▸ bc=129.732

   Dvs. |BC| = 129,7

Svar på opgave 8:

1. Kogetiden for et æg på 57 gram er f(57). Man får:

   f(x):=18.2*x^0.67 ▸ Udført

   f(57) ▸ 273.217

   Dvs. kogetiden er 273,2 min. for et æg på 57 g.

2. Man skal bruge formlen for procent-procent vækst: (1 + r_y) = (1 + r_x)^a, hvor man skal finde vækstraten for y, r_y, når vækstraten for x, r_x, er 15 %.

   Vækstraten for kogetiden er ((1 + 15 %)^0,67 - 1)·100 % = (1,15^0,67 - 1)·100 % = 9,816 %

   Dvs. det tager 9,8 % længere tid at koge ægget.

Svar på opgave 9:

1. Man opretter lister med antal dB og arbejdstiden ved hvert støjniveau.

   antaldb:={0,5,11,17,22,25} ▸ {0,5,11,17,22,25}

   arbejdstid:={1440,480,120,30,10,5} ▸ {1440,480,120,30,10,5}

   Man laver en eksponentiel regression på listerne:

   ExpReg antaldb,arbejdstid,1: CopyVar stat.RegEqn,f1: stat.results ▸
   [["Titel","Eksponentiel regression"]
   ["RegEqn","a*b^x"]
   ["a",1458.57]
   ["b",0.796877]
   ["r²",0.99994]
   ["r",−0.99997]
   ["Resid","{...}"]
   ["ResidTrans","{...}"]]

   Man får, at a = 0,7969 og b = 1458,6

   (Bemærk at Ti-Nspire buger a og b modsat opgaven.)

2. Det antal minutter man kan arbejde ved dette støjniveau er f(32):

   f1(32) ▸ 1.01965 (f1(x) er den regressionsfunktion som Ti-Nspire danner.)

   Dvs. man kan arbejde i 1 min.

3. Halveringskonstanten, K_1/2, findes ved hjælp af formlen: K_1/2 = ln(1/2)/ln(a):

   ln(0.5)/ln(0.796877) ▸ 3.05277

   Dvs. halveringskonstanten er 3,05 dB

   Dette tal betyder, at hver gang man øger støjniveauet med 3db over grænsen, så halveres den tid man maksimalt må arbejde ved dette støjniveau.

Svar på opgave 10:

1. Man skal finde rentesatsen, r, i formlen 360·(1+r)ⁿ = 179, hvor n = 2010 - 2004 = 6.

   solve(360.*(1+r)⁶=179,r) ▸ r=−1.89007 or r=−0.109928

   Da r ikke kan være mindre end -1 er den gennemsnitlige procentvise ændring = −0,1099 = -11 %

   (En gennemsnitlig procentlig årlig ændring på mindre end -1 (-100 %) svarer til, at man fjerner mere end det, der er at tage af.)

Svar på opgave 11:

1. f(x):=3190/(1+29.5*exp(−0.113*x)) ▸ Udført (f(x) oprettes)

   Kyllingens vægt 20 dage efter udklægningen er f(20):

   f(20) ▸ 782.181

   Dvs. kyllingens vægt efter 20 dage er 782 g

2. Man skal løse ligningen f(x) = 2500 med hensyn til x. Man får:

   solve(f(x)=2500,x) ▸ x=41.3429

   Dvs. kyllingen bliver 41 dage gammel

3. Væksthastigheden er f'(15). Man får:

   derivative(f(x),x)|x=15 ▸ 47.4252

   Dvs. væksthastigheden efter 15 dage er 47 g/dag

Svar på opgave 12:

1. f(x):=(2*x²-6*x)/(x²+1) ▸ Udført (opret f(x))

   Man finder x₁ og x₂ som nulpunkterne for f´(x):

   solve(derivative(f(x),x)=0.,x) ▸ x=−1.38743 or x=0.720759

   Dvs. x₁ = −1,387 og x₂ = 0,7208

2. Arealet er integralet ag f mellem x = (det største nulpuinkt for f) og x = 6. Man bestemmer nulpunkterne for f:

   solve(f(x)=0,x) ▸ x=0 or x=3

   Dvs. arealet er integralet af f fra x = 3 til x = 6:

   integral(f(x)*1.,x,3,6) ▸ 1.7618

   Dvs. arealet af området er 1,762