Svar på opgave 1:

1. y·(2·x - y) + (y - x)² =

   2·x·y - y² + y² - 2·x·y + x² =

   (2·x·y - 2·x·y) + (y² - y²) + x² =

   0 + 0 + x² =

   x²

Svar på opgave 2:

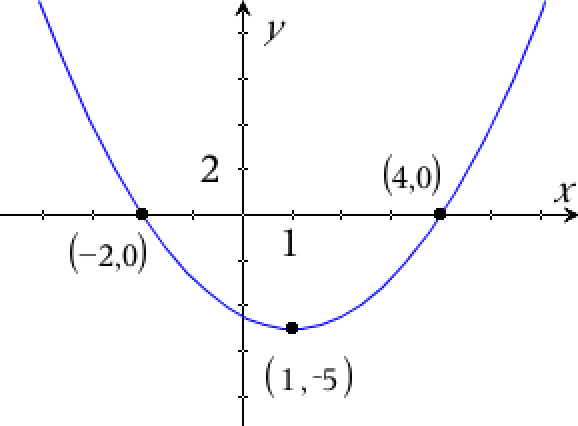
1. Det at f har rødderne -2 og 4 betyder, at grafen til f går igennem punkterne (-2,0) og (4,0). Disse punkter tegnes ind i et koordinatsystem sammen med toppunktet (1,-5).

   Man tegner en parabel gennem punkterne som vist nedenunder.

   

Svar på opgave 3:

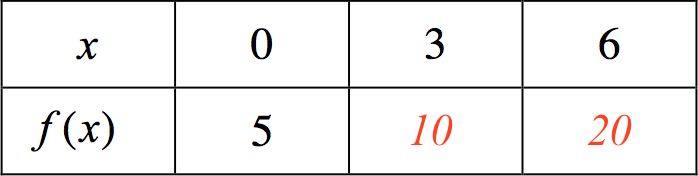
1. Det at fordoblingskonstanten er 3 betyder, at f(x) fordobles, hver gang man lægger 3 til x.

   Man får derfor at f(3) = 10 og f(6) = 20. Nedenfor er skemaet udfyldt.

   

Svar på opgave 4:

1. For x = 0 er y = 30 og for x = 25 er y = 80. Man skal derfor løse de to sammenhørende ligninger

   a·0 + b = 30 ∧ a·25 + b = 80 med hensyn til a og b. Man får:

   a·0 + b = 30 ∧ a·25 + b = 80 ⇔

   b = 30 ∧ a·25 + b = 80 ⇔

   b = 30 ∧ a·25 + 30 = 80 ⇔

   b = 30 ∧ a·25 = 80 - 30 ⇔

   b = 30 ∧ a·25 = 50 ⇔

   b = 30 ∧ a = 50/25 ⇔

   a = 2 ∧ b = 30

Svar på opgave 5:

1. Det ses af nedenstående figur at f(1) = -3 (vist med grøn ring) og f´(1) = 0 (vist med blå streg).

   

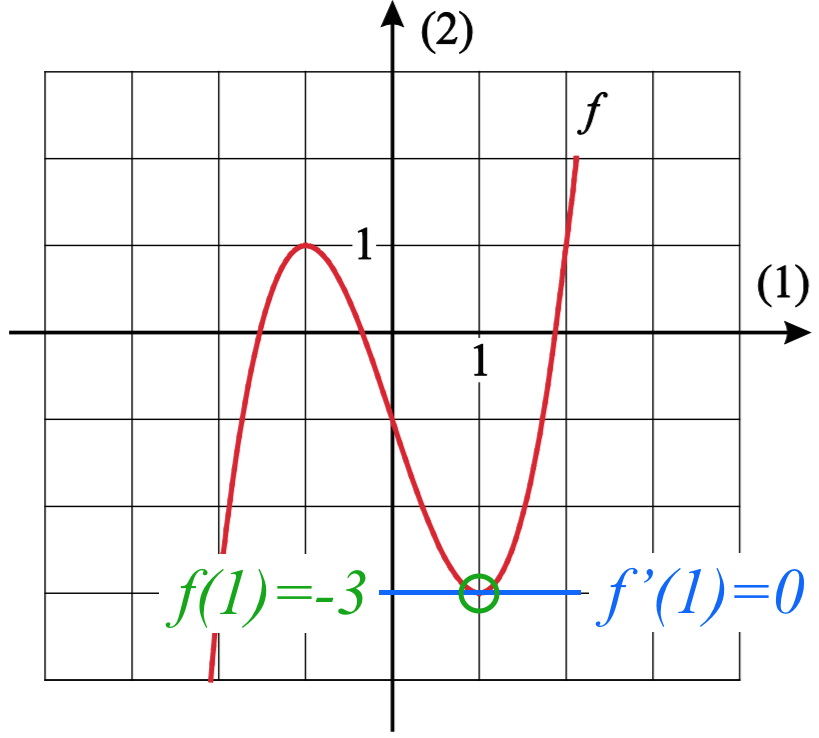
   f(1) er funktionsværdien i et lokalt minimum, hvor x = 1, og f´(1) er grafens hældning for x = 1.

Svar på opgave 6:

1. Funktionen g(x) en stamfunktion til f(x), hvis g'(x) = f(x). Man får:

   g'(x) = [(3/2)·x² + 4·x + 3]' = 3·x + 4 = f(x), hvilket viser, at g(x) er en stamfunktion til f(x).

   

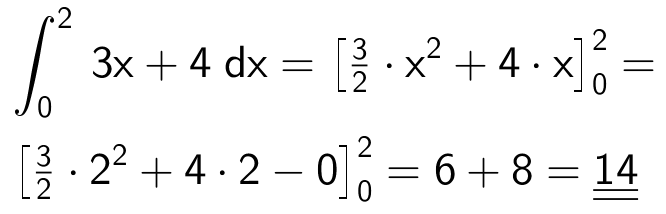
Svar på opgave 7:

1. Der er tale om en aftagende lineær sammenhæng f(x) = a·x + b, idet der forsvinder en fast mængde pr. tidsenhed. f(x) er den tilbageværende mængde af saltvand i mL og x er antal minutter.

   Man skal finde a og b, idet man ved at: 790 = a·30 + b og 655 = a·60 + b. Man får følgende:

   f(x):=a*x+b ▸ Udført ...opret f(x)

   solve(f(30)=790 and f(60)=655,a,b) ▸ a=−9/2 and b=925 ...løs ligninger med hensyn til a og b

   Formlen er f(x) = -4,5·x + 925

2. Mængden af saltvand som patienten får pr. minut er lig med -a i formlen for f(x), dvs. 4,5 mL/min.

   Den mængde saltvand, som der var i flasken til at starte med, var f(0) = -4,5·0 + 925 = 925, dvs. den var 925 mL

Svar på opgave 8:

Tegningen fra opgaven gengives som hjælp:



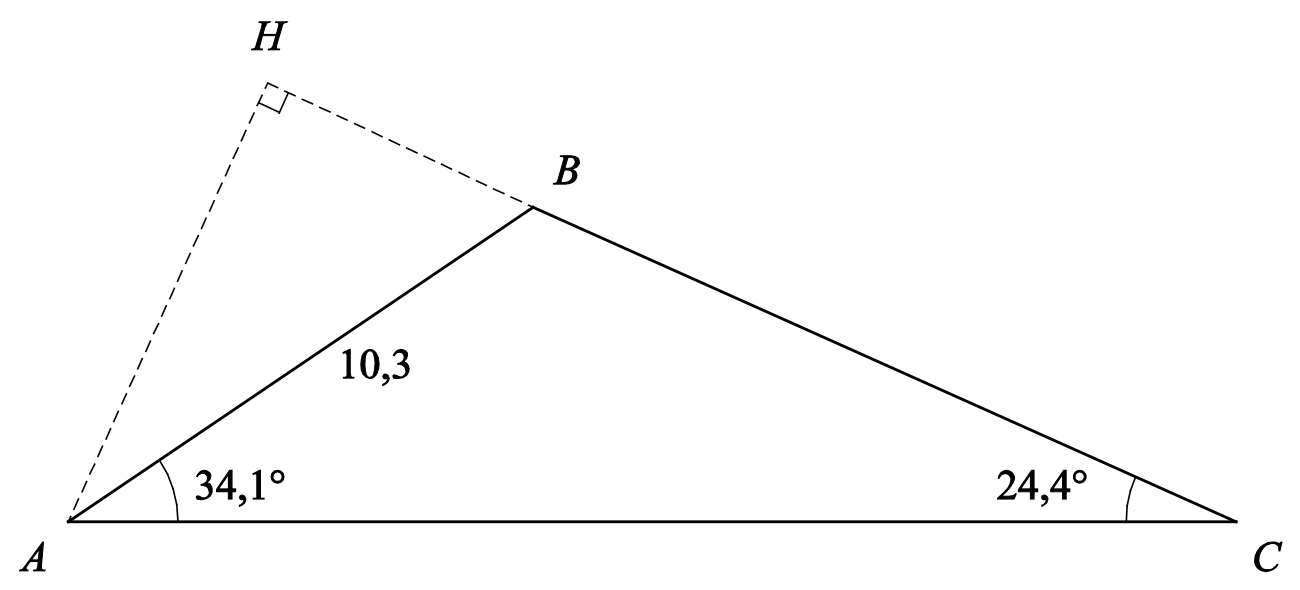
1. For at bestemme længden af siden BC bruger man en sinusrelation:

   solve(sin(34.1°)/bc=sin(24.4°)/10.3,bc) ▸ bc=13.9785 ...hvor bc = |BC|

   Dvs. |BC| = 14,0

2. For at bestemme længden af højden AH finder man først |AC| ved hjælp af en sinusrelation. Her skal man desuden bruge reglen om at vinkelsummen i en trekant er 180°, der giver at vinkel B er 180° - 34,1° - 24,4° = 121,5°. Man får:

   solve(sin(121.5)/ac=sin(24.4°)/10.3,ac) ▸ ac=21.2733 ...hvor ac = |AC|

   Dernæst beruger man følgende geometriske sammenhæng for en retvinklet trekant: modstående katete til en vinkel = hypotenuse gange sinus til vinklen, der her giver: |AH| = |AC|·sin(C), dvs

   |AH| = 21.2733·sin(24,4°) = 8,7881

   Dermed er |AH| = 8,79

Svar på opgave 9:

1. 300841 er startværdien, dvs. y-værdien når x = 0, der her svarer til antal brugere i december 2007.

   Tallet 1,147 er den månedlige fremskrivningsfaktor, dvs. det tal man ganger den gamle måneds tal med for at få den nyes.

   (Trækker man 1 fra fremskrivningsfaktoren, så får man den månedlige væsktrate: 1,147 - 1 = 0,147 = 14,7 %).

2. For at finde antallet af måneder, der går før antallet af danske brugere kommer over 1 million, skal man løse ligningen: 300.841·(1.147)^x = 1.000.000:

   solve(300841*(1.147)^x=1000000,x) ▸ x=8.75811

   Dvs, der går 8,8 måneder før antallet af brugere kommer over 1 mio.

3. For at finde ud af, hvor mange brugere af Facebook, der er efter 22 måneder, så indsætter man x = 22 i formlen:

   300841*(1.147)^x|x=22 ▸ 6.14798E6

   Dvs. der vil i følge modellen være 6,15 mio. brugere efter 22 måneder.

   Dette tal er højere end det faktiske, dvs. modellen rammer for højt.

Svar på opgave 10:

1. Man finder monotoniforholdene ved at lave en fortegnsundersøgelse for f´(x).

   f(x):=0.5*x³-3*x²+4.5*x+2 ▸ Udført ...man opretter f(x)

   solve(derivative(f(x),x)=0,x) ▸ x=1. or x=3. ...f´(x)=0 har løsningerne x=1 eller x=3

   derivative(f(x),x)|x=0 ▸ 4.5 ...f´(x)=4,5 for x=0, dvs. f´(x)>0 for x<1

   derivative(f(x),x)|x=1.5 ▸ −1.125 ...f´(x)<0 for 1 < x < 3

   derivative(f(x),x)|x=4 ▸ 4.5 ...f´(x)>0 for x > 3

   Ud fra denne undersøgelse af f´(x) får man følgende monotoniforhold:

   f er voksende for x<1, f er aftagende for 1<x<3 og f er voksende for x>3

2. Tangenten til f gennem punktet (0,2) har ligningen y = f'(0)·x + 2 ⇒ y = 4,5·x + 2

   idet vi ovenfor fandt at f´(0) = 4,5.

   (I Ti-Nspire kan man også benytte: tangentLine(f(x),x,0) ▸ 4.5*x+2)

3. Man skal finde det x, hvor f'(x) = 4,5 og x er forskelligt fra 0:

   solve(derivative(f(x),x)=4.5 and x≠0,x) ▸ x=4.

   Dvs. førstekoordinaten til røringspunktet er 4 og andenkoordinaten er f(4) ▸ 4.

   Røringspunktet for den anden tangent er dermed (4,4)

Svar på opgave 11:

1. Man skal løse følgende to ligninger: b·60^a = 26 og (1,2)^a - 1 = 0,44. Den sidste kommer af procent-procent vækst-formlen for potensfunktioner: (1+r_y)=(1+r_x)^a, hvor r_y = 44% er vækstprocenten for bremselængden og r_x = 20% er vækstprocenten for hastigheden.

   Man får:

   solve(b*60^a=26 and (1.2)^a-1=0.44,a,b) ▸ a=2. and b=0.007222

   Dvs. a = 2 og b = 0,00722

Svar på opgave 12:

1. f(x):=e^(x) ▸ Udført ...opret f(x)

   g(x):=−3*x²+6*x ▸ Udført ...opret g(x)

   Man bestemmer x-værdierne af skæringspunkterne for graferne af f og g:

   solve(f(x)=g(x),x) ▸ x=0.241233 or x=1.09041

   Dvs. f(x) = g(x) har løsningerne x = 0,2412 eller x = 1,0904

   Arealet der afgrænses af f og g er integralet af f(x)-g(x) fra x = 0,241233 til x = 1,09041. Man får:

   integral(g(x)-f(x),x,0.241233,1.09041) ▸ 0.407273

   Dvs. arealet er 0,407

Svar på opgave 13:

1. Man skal betstemme x i ligningen, når y = 21,5.

   solve(log(21.5,10)=0.59*log(x,10)+0.18,x) ▸ x=89.8019 ...hvor log() er 10-tals logaritmen

   Dvs. arealet af flodbassinet er 89,8 km³

2. Man isolerer y i formlen for sammenhængen mellem længste vandløb og bassinets areal:

   solve(log(y,10)=0.59*log(x,10)+0.18,y) ▸ y=1.51356*x^0.59 and x≥0.

   Dvs. a = 0,591,514