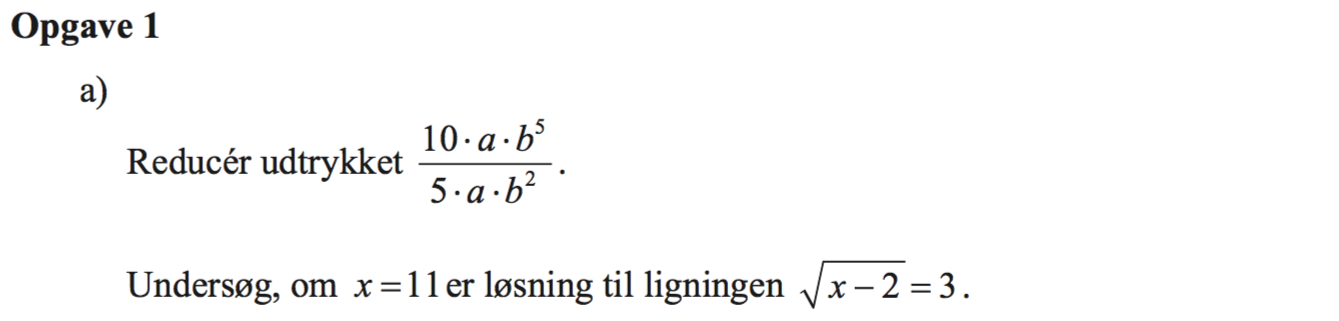
Svar på opgave 1:

1. (10·a·b⁵)/(5·a·b² = (2·[5·a·b²]·b³)/(5·a·b² = 2b³

   Man gør prøve:

   Venstre side: √[11 - 2] = √[9] = 3

   Højre side: 3

   Da venstre og højre side giver det samme, er x = 2 en løsning.

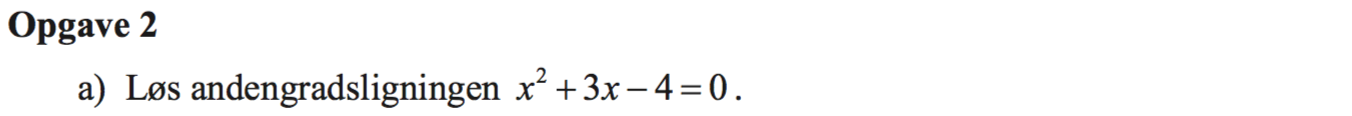
Svar på opgave 2:

1. x² + 3x - 4 = 0 ⇔

   x = -3/2 ± √[3² - 4·(-4)]/2 ⇔

   x = -3/2 ± √[25]/2 ⇔

   x = -3/2 ± 5/2 ⇔

   x = -3/2 - 5/2 ∨ x = -3/2 + 5/2 ⇔

   x = -8/2 ∨ x = 2/2 ⇔

   x = -4 ∨ x = 1

Svar på opgave 3:

1. Det bestemte integrale giver:

   

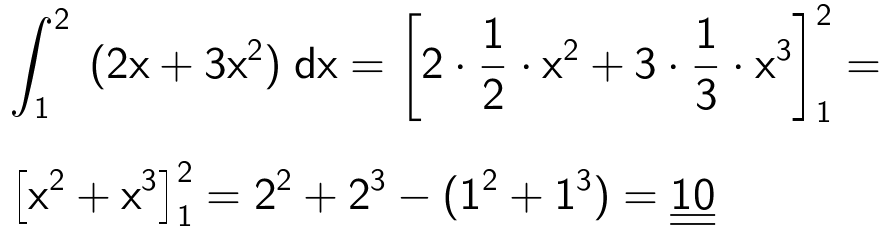
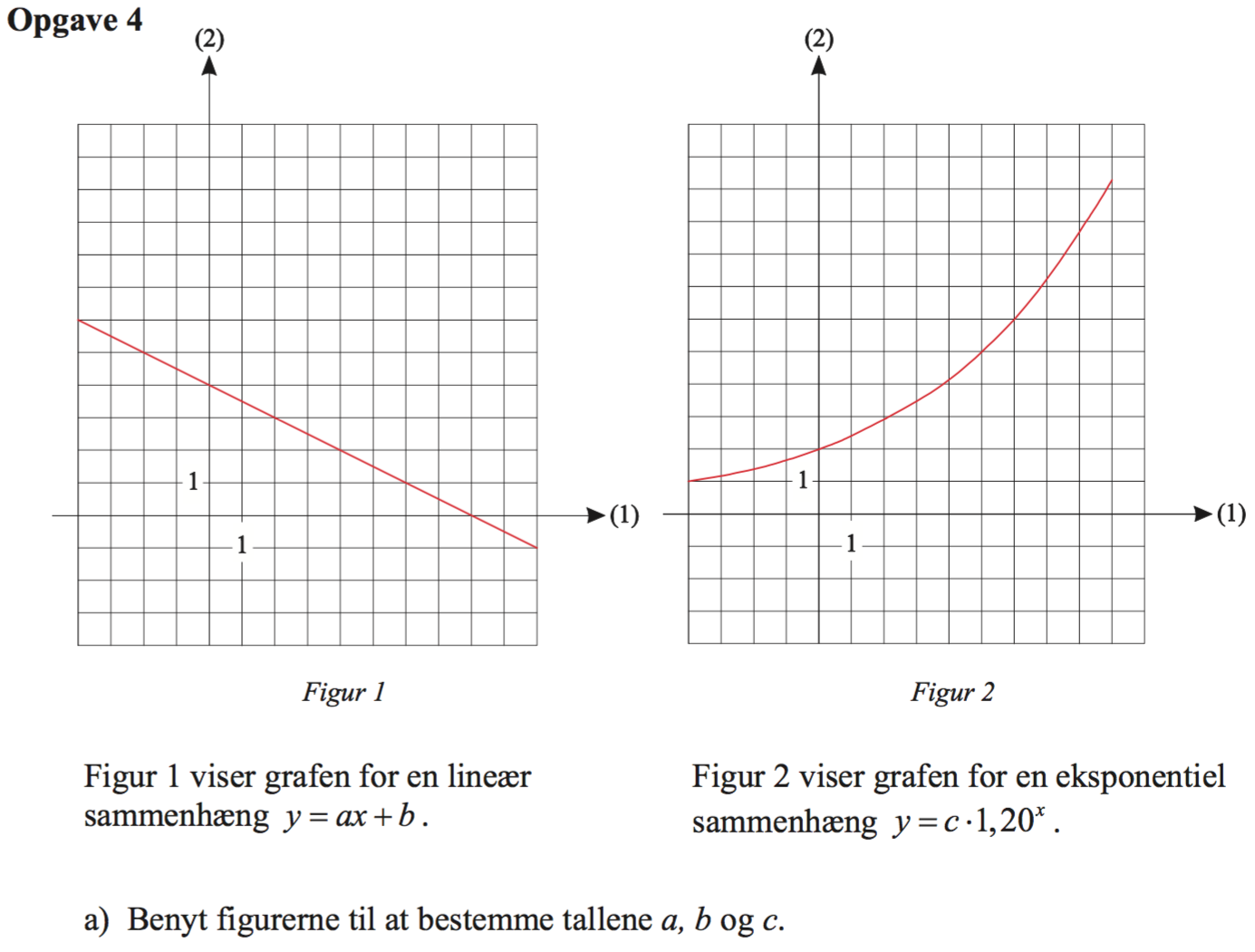
Svar på opgave 4:

1. Konstanterne a og b findes af den venstre graf og c findes af den højre. Dette er vist nedenunder, idet akserne er fremhævet med blåt:

   

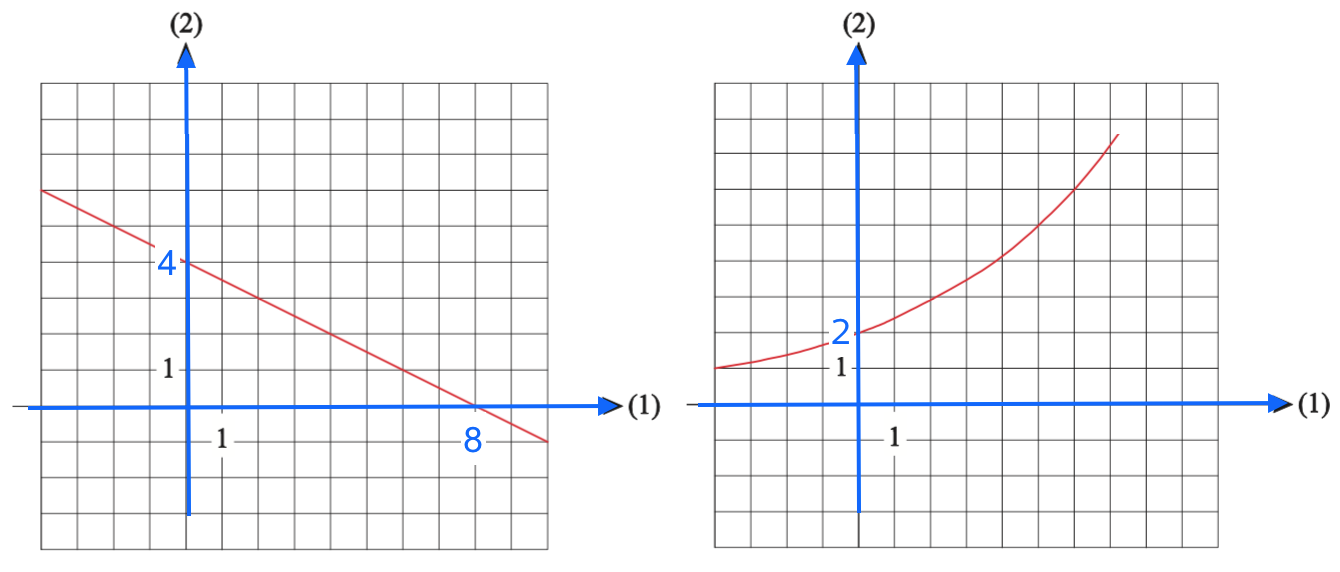
   Konstanten a er hældninger til den rette linje, som er (0 - 4)/8 = -1/2. Konstanten b er linjens skæring med y-aksen, som aflæses til 4. Konstanten c er den eksponentielle kurves skæring med y-aksen (x = 0 ⇒ y = c·1,2⁰ = c). Denne værdi aflæses til c = 2.

   Dvs. a = -1/2, b = 4 og c = 2

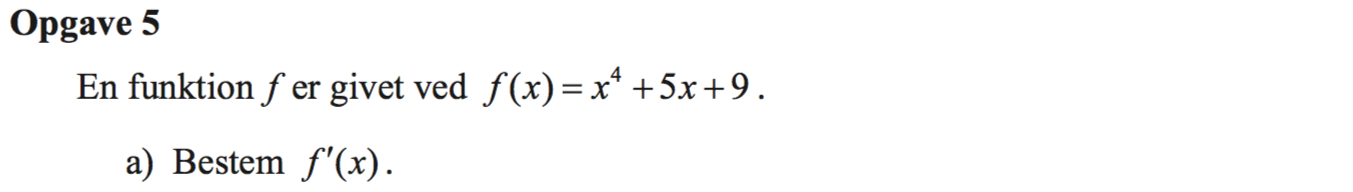
Svar på opgave 5:

1. f´(x) = (x⁴ + 5x + 9)' = 4x³ + 5,

Svar på opgave 6:

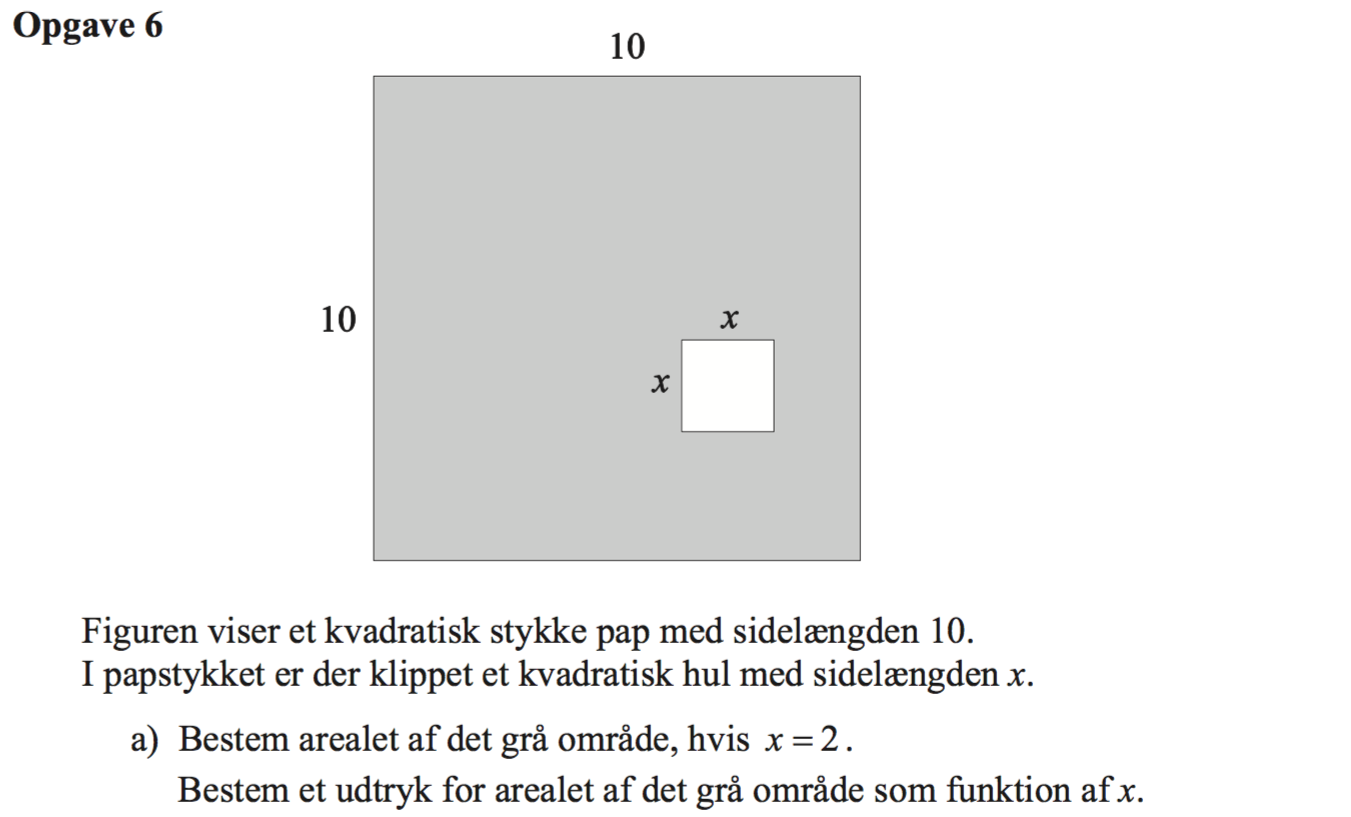
1. (I omvendt rækkefølge:) Det store kvadrat har arealet 10² = 100, men det lille har arealet x². Det grå område har dermed arealet:

   100 - x²

   Indsættes x = 2 får man arealet af det grå område til 100 - 2² = 100 - 4 = 96

Svar på opgave 7:

1. Man opretter lister over hundenes vægt og fordermængderne og laver en potensregression på listerne i Ti-Nspire som vist nedenunder:

   

   (Menu-stien til kommandoen, når man står i Noter er: Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Potensregression... hvorpå man vælger de to lister).

   Det ses af resultatskemaet at a = 0,74723 og b = 25,260 (Ti-Nspire bruger a og b modsat opgaven.)

2. Man skal bruge formlen for procent-procent vækst for potensfunktioner. F_y = (F_x)^a. Her er

      F_y fremskrivningsfaktoren for den store hunds fodermængde,

      F_x er fremskrivningsfaktoren for den store hunds vægt, som er 1 + 30 % = 1,30 og

      a er 0,74723.

   Dette giver: F_y = 1,30^0,74723 = 1,21658.

   Dvs. den store hunds fodermængde er (1,21658 -1)·100 % = 22 % større end den lille hunds.

Svar på opgave 8:

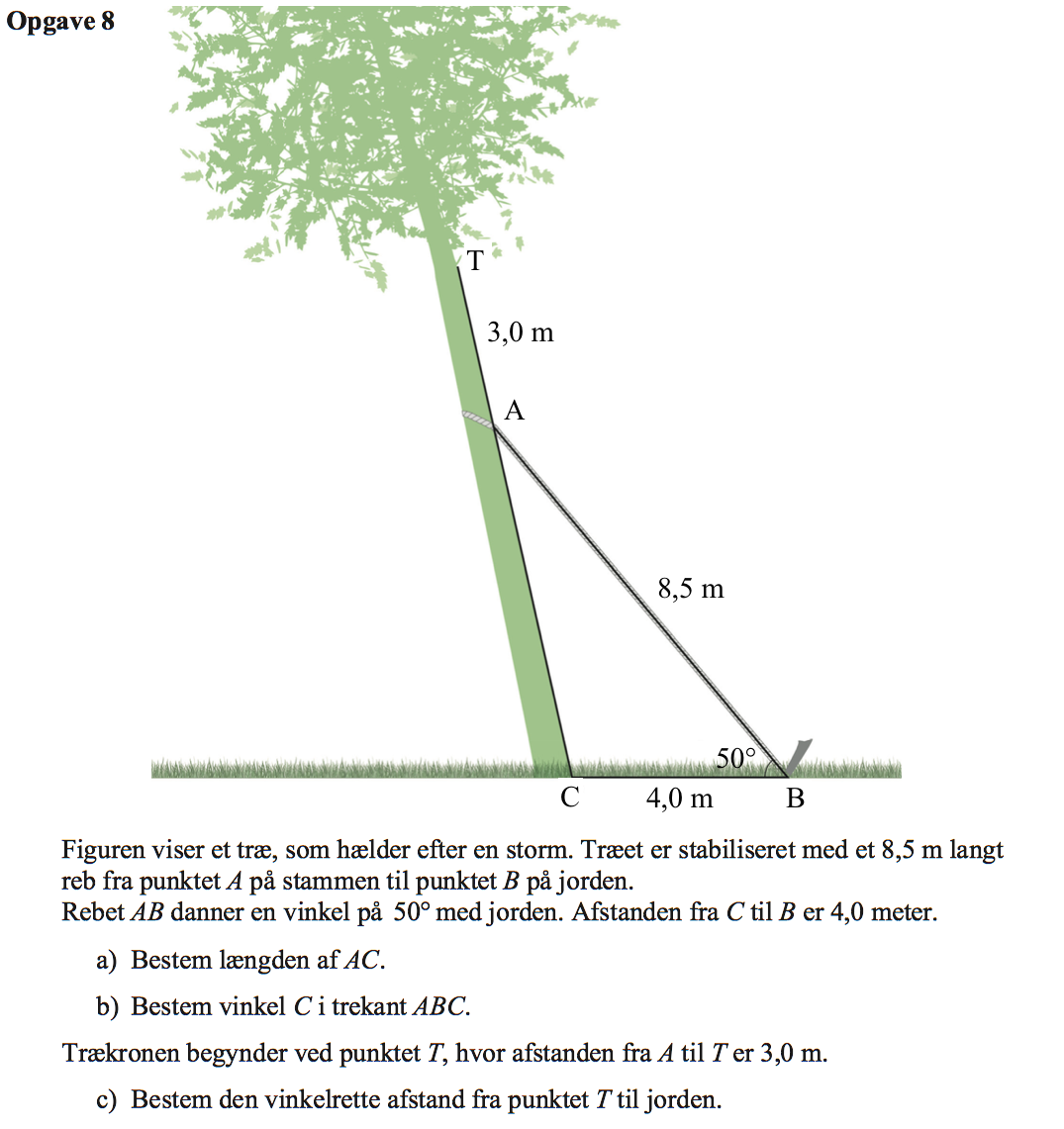
1. For at finde |AC| skal man bruge en cosinusrelation, idet man kun medtager positive løsninger. Dette gøres i Ti-Nspire:

   solve(cos(50°)=(8.5²+4²-ac²)/(2*8.5*4),ac)|ac>0 ▸ ac=6.67386

   Dvs. |AC| = 6,67

2. For at finde vinkel C i ΔABC skal man bruge en sinusrelation. Det antages at ∠ACB er stump fordi træet er bøjet. Bregningen foretages i Ti-Nspire:

   solve((sin(50°)/6.67386)=(sin(c*1.°)/8.5),c)|90<c<180 ▸ c=102.669

   Dvs. vinkel C = 102,7°

3. Den viklerette afstand fra T til jordens findes som længden af siden HT i den retvinklede trekant CHT som vist på figuren nedenunder:

   

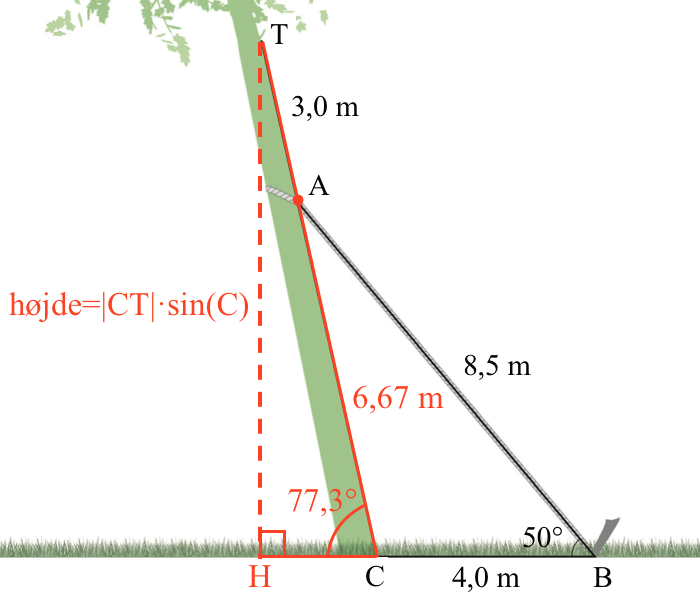
   Man bruger en trigonometrisk formel for en retvinklet trekant: c = hypotenuse·sin(C) og får:

   |HT| = (6,6739 + 3)·sin(180° - 102,67°) = (6,6739 + 3)·sin(77,331°) = 9,4383

   Dvs. den vinkelrette afstand er 9,44 m

Svar på opgave 9:

1. Man starter med at oprette f(x) i Ti-Nspire:

   f(x):=(1/4)*x²+ln(x) ▸ Udført

   Tangentens ligning findes ved hjælp af kommandoen tangentLine() i Ti-Nspire (man skriver "y=" foran kommandoen for at få hele ligningen skrevet ud)

   y=tangentLine(f(x),x,4.) ▸ y=2.25*x-3.61371

   Dvs. tangentens ligning gennem punktet (4,f(4)) er y = 2,25·x-3,614

2. Man starter med at finde de x-værdier, hvor kurvens hældning (f´(x)) og dermed også tangentens hældning er 1,5. Dette gøres ved hjælp af solve()-kommandoen:

   solve(derivative(f(x),x)=1.5,x) ▸ x=1. or x=2.

   Dvs. x-værdierne er x = 1 og x = 2. De tilhørende y-værdier findes:

   f(1.) ▸ 0.25 f(2.) ▸ 1.69315

   Dvs. de punkter, hvor tangentens hældninger 1,5 er (x,y) = (1;0,25) og (x,y) = (2;1,693)

Svar på opgave 10:

1. 490 er den årlige faste vækst i antal lobbyister og 10400 er startværdien dvs. antallet af lobbyister i 2008.

2. Man skal løse de sammenhørende ligninger: g(0) = b·a⁰ = 1450 og g(9) = b·a⁹ = 2750 med hensyn til a og b. Dette gøres i Ti-Nspire:

   

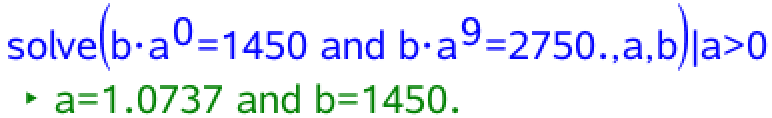
   Dvs. a = 1,0737 og b = 1450

   (Bemærk betingelsen |a>0 efter solve()-kommandoen. Den er ikke nødvendig, men er medtaget for at undgå at få en gul advalsestrekant, der ikke ser pæn ud.)

3. Man opretter funktionerne f(x), g(x) og h(x) i Ti-Nspire:

   

   

   

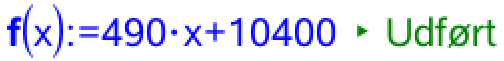
   Man skal løse ligningen h(x) = 0,175 med hensyn til x for x > 0. (Kun positive x er gyldige).

   

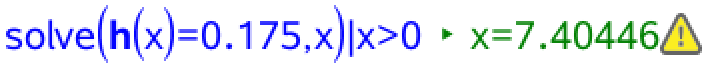
   Det ses at der går 7,4 år før det sker. Man skal nu runde op til nærmeste hele antal år, som er 8, og lægge dette til 1998 for at få årstallet. Dette giver året: 1998 + 8 = 2006, er det år, hvor det gennemsnitlige budget for en lobbyist overstiger 0,175 mio. dollars.

   (Man kan kontrollere, at man skal runde op ved at beregne h(7) = 0,172, som ses at være mindre end 0,175).

Svar på opgave 11:

1. En eksponentiel udvikling betyder, at både befolkningen i Sverige og Ungarn følger formlen:

   y = b·a^x, hvor Sverige og Ungarn har hvert sit a og b.

   Tallet b er startværdien dvs. befolkningstallet for x = 0 eller år 2009. For Sverige er b: 9,348 mio. og for Ungarn er b: 10,014 mio.

   Tallet a er fremskrivingsfaktoren dvs.: 1 + vækstraten. For Sverige giver a: 1 + 0,3 % = 1 + 0,003 = 1,003 og for Ungarn giver a: 1 + (-0,3 %) = 1 - 0,003 = 0,997.

   Man opretter funktionerne f(x) for Sveriges befolkningsudvikling og g(x) for Ungarns i Ti-Nspire:

   

   

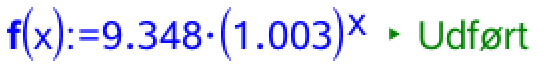
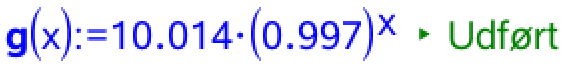
   Sveriges befolkningstal i 2018 bliver i følge formlen:

   

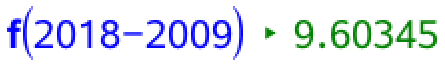
   Dvs. der er 9,60 mio. mennesker i Sverige i 2018.

2. For at finde det år hvor Sveriges befolkningstal overstiger Ungarns skal man først løse ligningen f(x) = g(x).

   

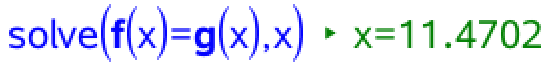
   Dvs. Sveriges befolkning overgår Ungarns efter 11,4 år. Man skal nu undersøge om man skal runde op eller ned for at få det rigtige årstal. Man finder, at f(11) < g(11), mens f(12) > g(12):

   

   Dvs. man skal runde x op til 12 for at få et år, hvor Sveriges befolkning overgår Ungarns.

   Dermed er året 2009 + 12 = 2021

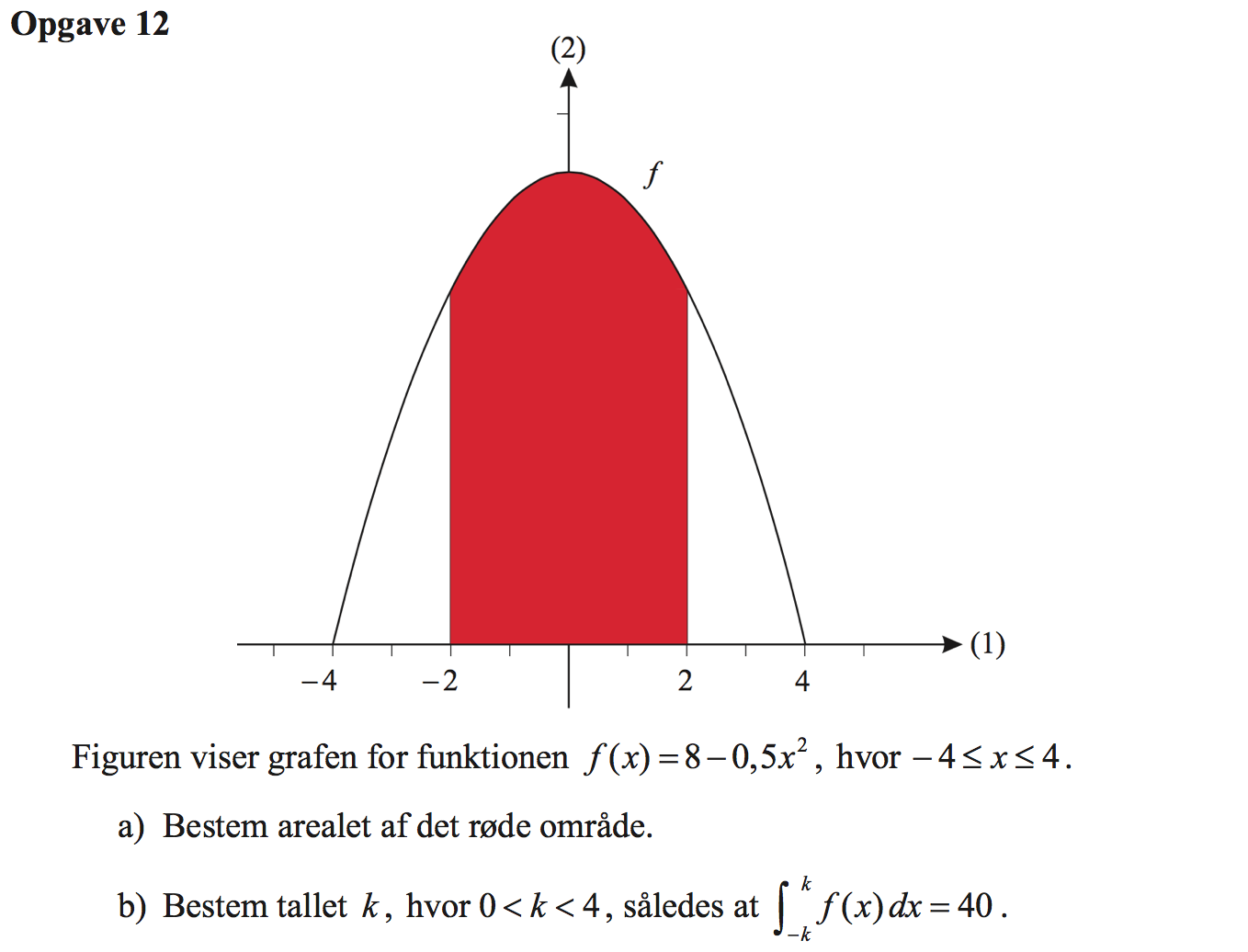
Svar på opgave 12:

1. Man opretter f(x) i Ti-Nspire:

   

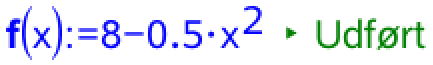
   Arealet af det røde område er integralet af f(x) fra x = -2 til x = 2:

   

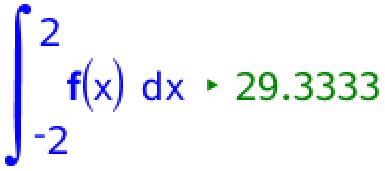
   Arealet af det røde område er 29,33

2. Man løser ligningen med hensyn til k i Ti-Nspire som vist:

   

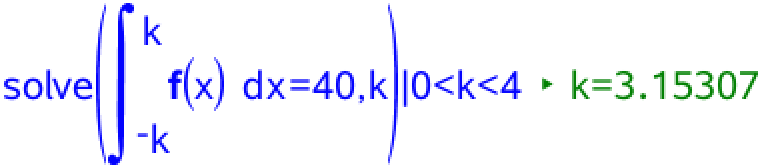
   Dvs. k = 3,15