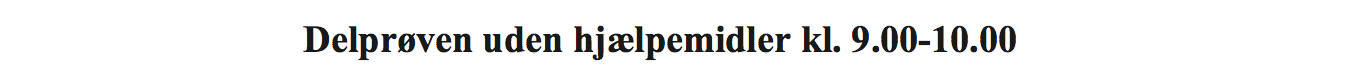
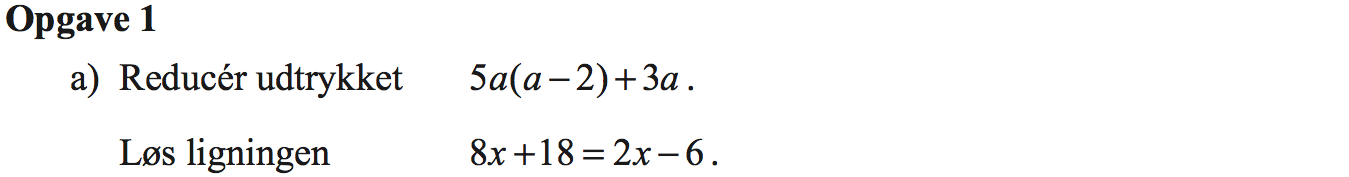
Svar på opgave 1:

1. 5a(a - 2) + 3a =

   5·a·a - 5·a·2 + 3·a=

   5·a² - 10·a + 3·a =

   5a² - 7a

2. 8x + 18 = 2x - 6 ⇔

   8x - 2x = -6 - 18 ⇔

   6x = -24 ⇔

   x = -4

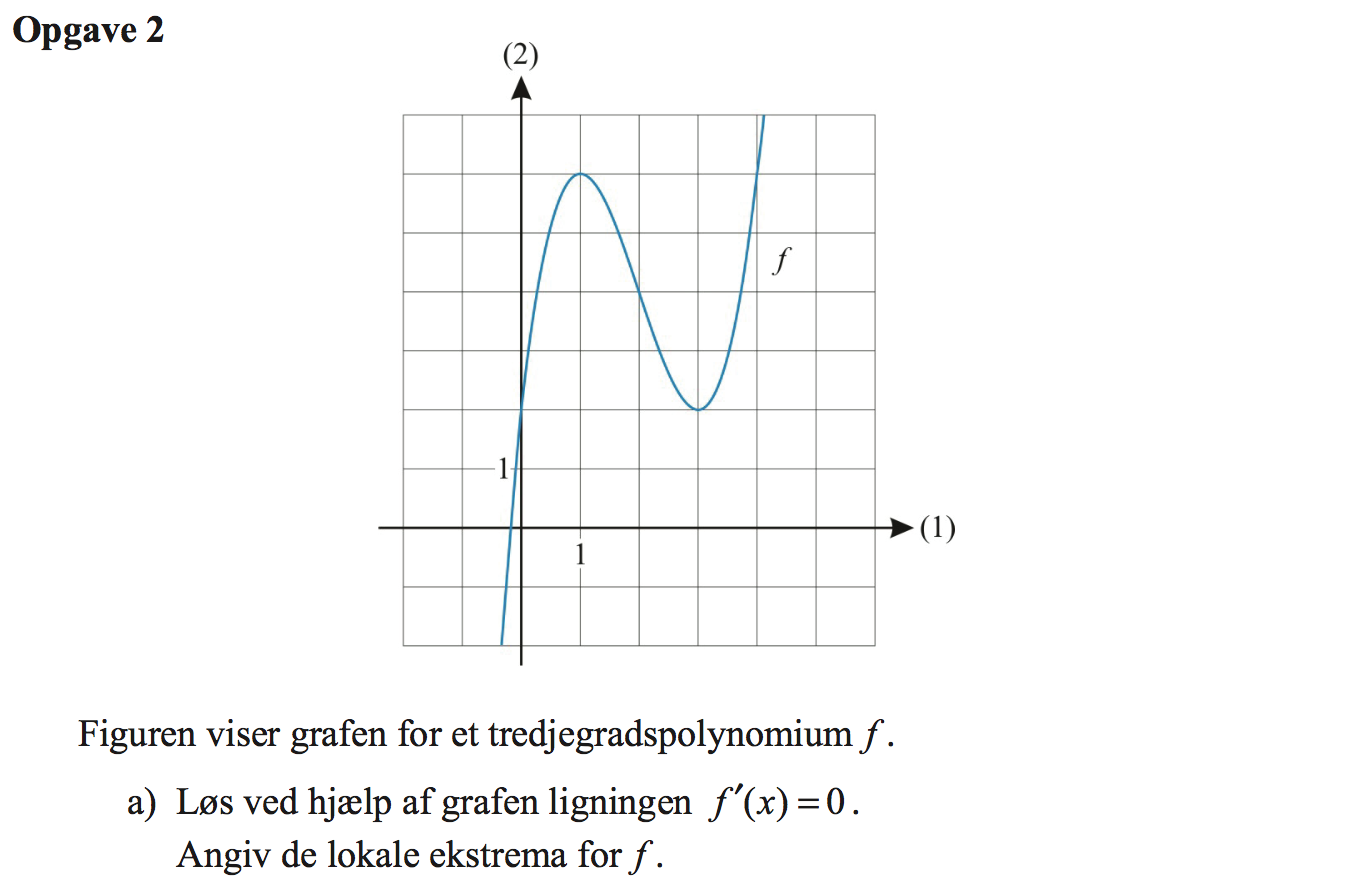
Svar på opgave 2:

1. Løsningen til ligningen f´(x) = 0 er de x-værdier, hvor kurvens hældning er nul eller kurvens tangent er vandret. Dette er undersøgt på nedenstående tegning:

   

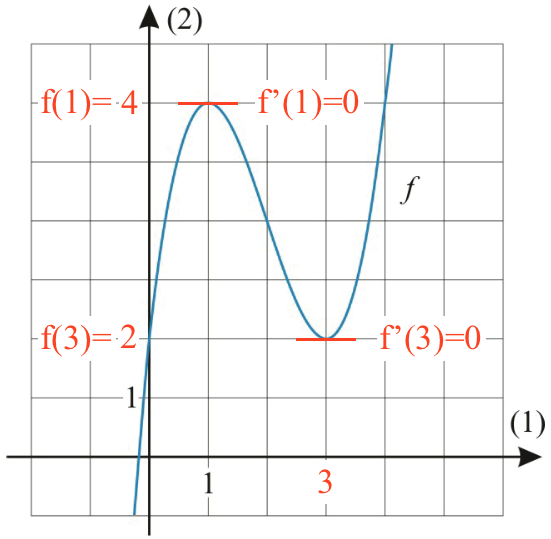
   Dvs. f´(x) = 0 for x = 1 og x = 3

   (Der menes nok y-værdierne for de lokale ekstrema.) Man får de lokale ekstrema til:

   f(1) = 4 (lokalt maksimum) og f(3) = 2 (lokalt minimum).

Svar på opgave 3:

1. Der er tale om en faldende eller aftagende eksponentiel udvikling (udvikling med procentuel ændring), hvor vækstraten er -3 % (der sker et fald på 3 % om året i antal enheder).

   Formlen er y = b·a^x, hvor b er begyndelsesværdien, dvs. antal enheder for x = 0, som her er år 2005. Tallet a er fremskrivningfaktoren: 1 + vækstrate = 1 + (-3 %) = 1- 0,03 = 0,97. y er antal enheder et givet år og x er antal år efter 2005.

   Det giver: y = 126000·0,97^x, x≥0

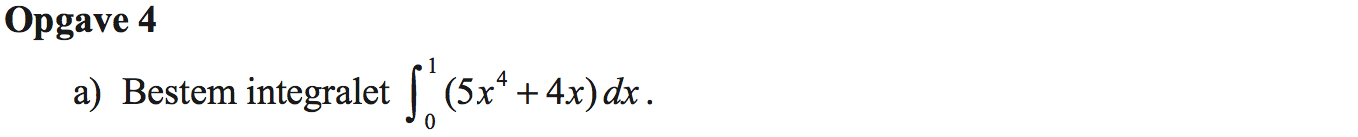
Svar på opgave 4:

1. Integralet er :

   

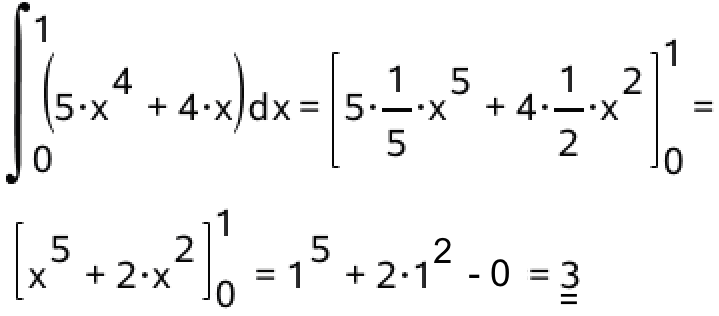
Svar på opgave 5:

1. f´(x) = (x³ + x - 2)' = 3x² + 1. Da x² er større end eller lig med nul for alle x er f´(x) størren end 0 for alle x. Dette viser at f(x) er voksende for alle x.

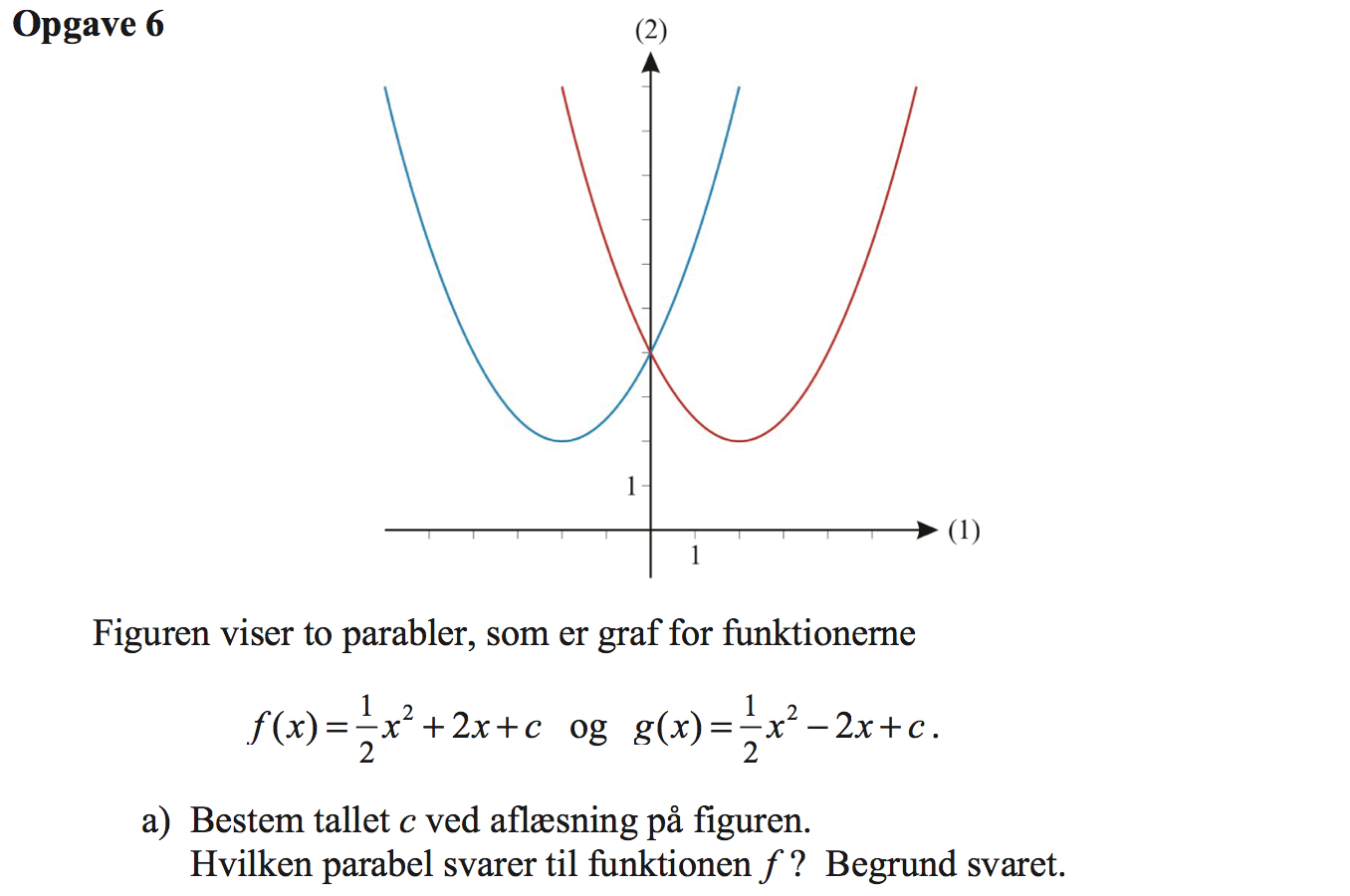
Svar på opgave 6:

1. c er y-værdien for grafens skæring med y-aksen. Dvs. c er 4 for begge funktioner.

   For f er b > 0. Da b er hældninbgen for funktionen ved skæringen med y-aksen svarer den blå kurve til f

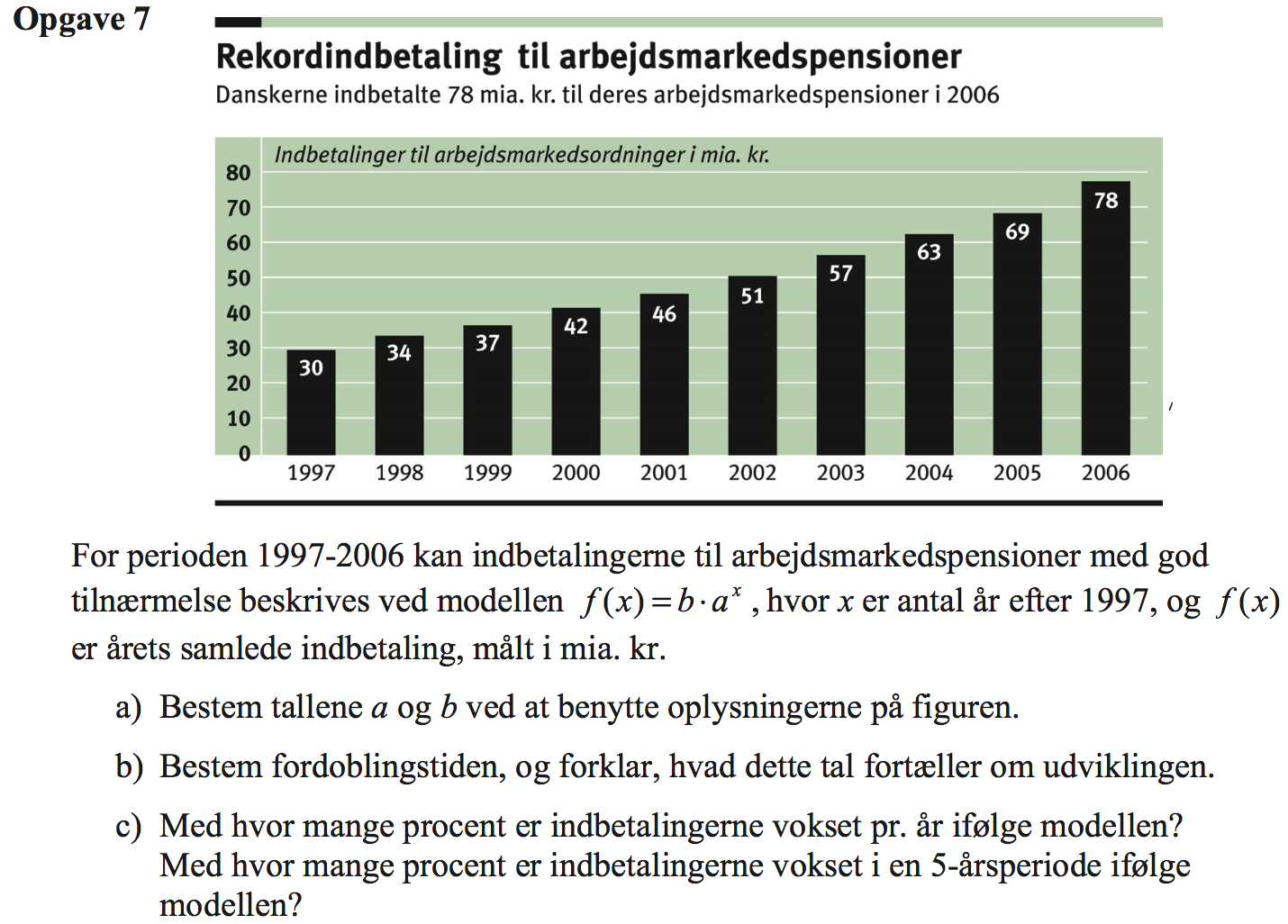
Svar på opgave 7:

1. Man opretter en liste for x, som er antal år efter 1997 kaldet "år". Derudover opretter man en liste for y kaldet "indbetaling". På disse lister laver man en eksponentiel regression. Dette er gjort i Ti-Nspire nedenunder:

   

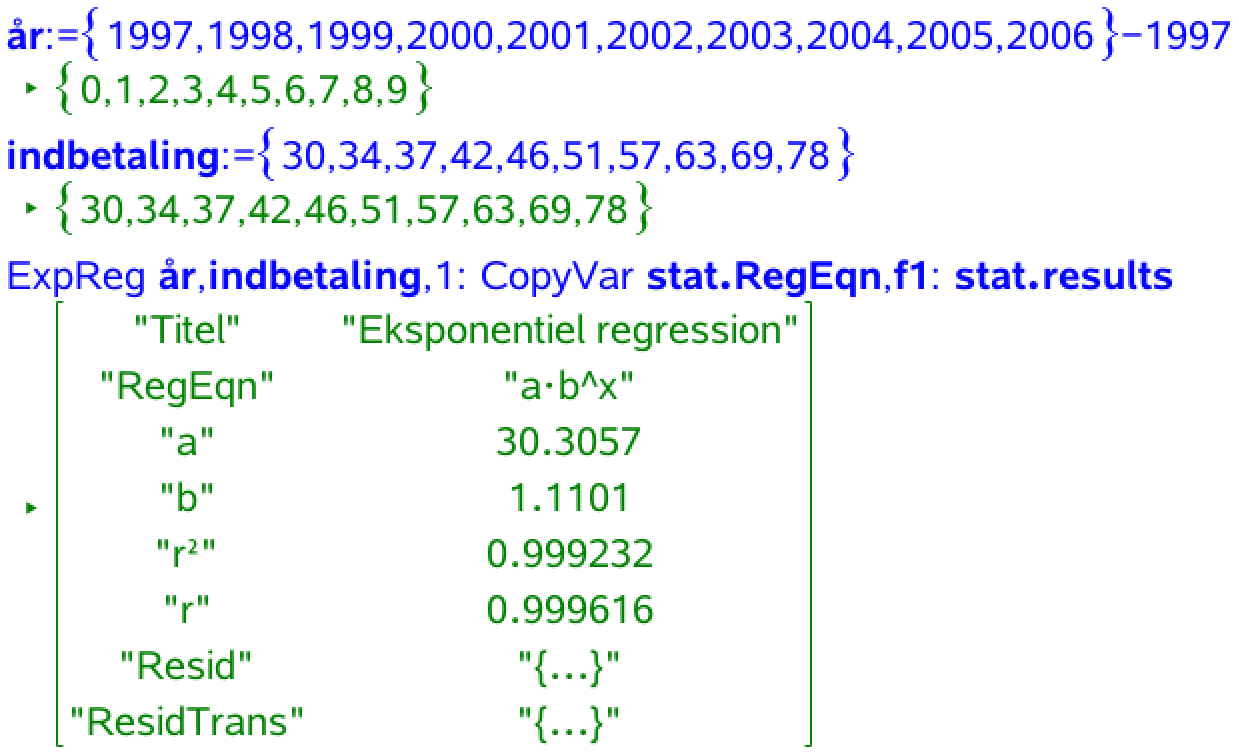
   (Menu-stien til kommandoen, når man står i Noter er: Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Eksponentiel regression... hvorpå man vælger de to lister).

   Det ses af resultatskemaet, at a = 1,1101 og b = 30,306 (Ti-Nspire bruger a og b modsat opgaven).

2. Fordoblingstiden er ln(2)/ln(a) år = ln(2)/ln(1,1101) år = 6,6 år

3. Årlig procentvis vækst = a - 1 = 1,1101 - 1 = 0,1101 = 11 %

   Den samlede procentuelle vækst i en 5-årig periode er (uafhængigt af hvor man starter):

   (100 %)·[y(x + 5) - y(x)]/y(x) =

   (100 %)·[30,306·1,1101^{x + 5} - 30,306·1,1101^x]/(30,306·1,1101^x) =

   (100 %)·[1,1101⁵ - 1] =

   (100 %)·[1,6858 - 1] =

   68,6 %

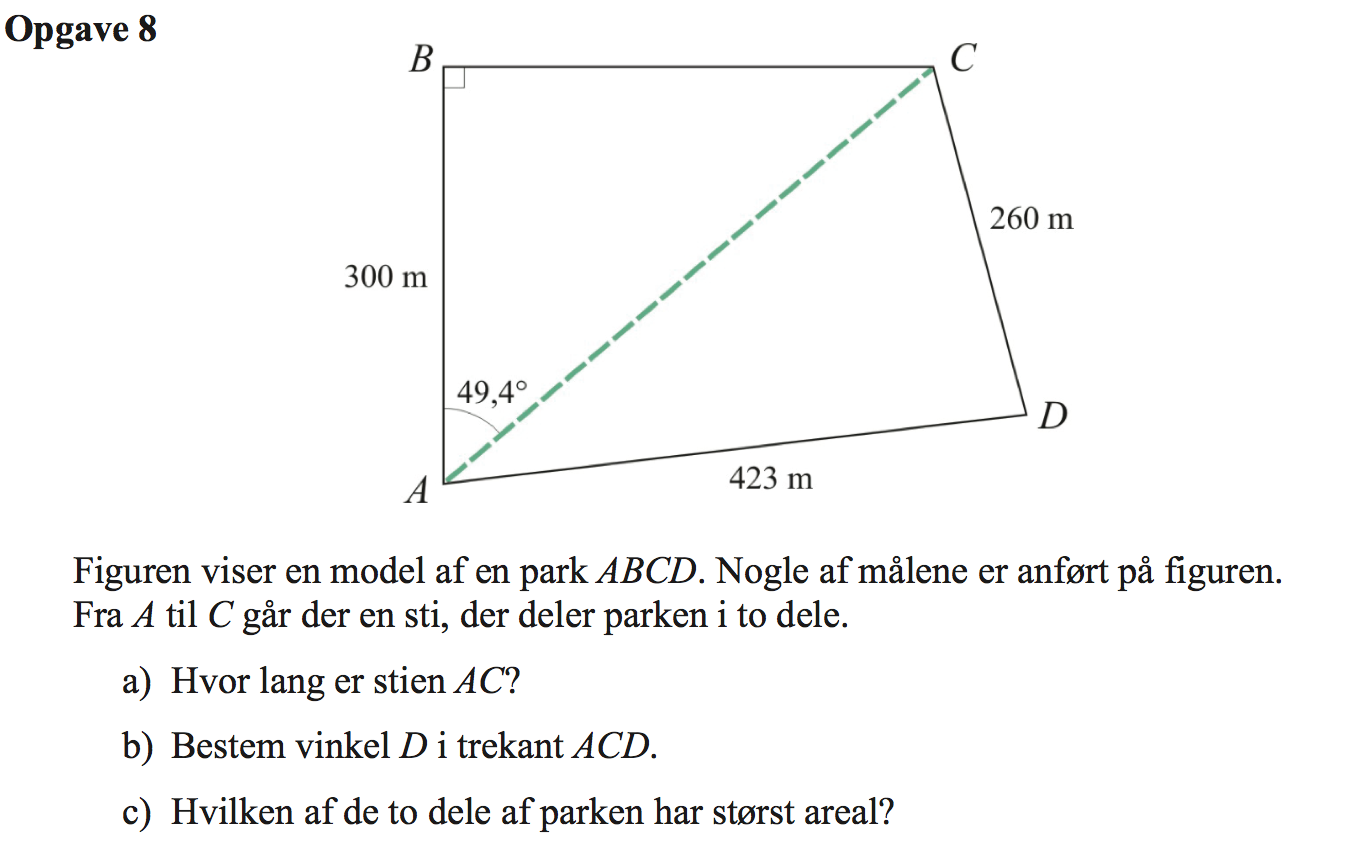
Svar på opgave 8:

1. Man skal bruge både en en cosinus relation som vist

   

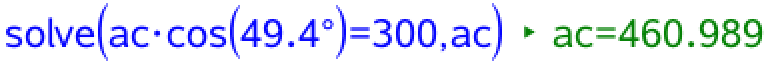
   Man kan også bruge en sinus relatio, idet man bruger reglen om at vinkelsummen i en trekant (som her ΔABC) er 180°:

   

   Det ses at |AC| = 461,0

2. ∠D bestemmes ved hjælp af en cosinusrelation i Ti-Nspire:

   

   Dvs. ∠D = 81,1°

3. Arealet af en trekant er 0,5·grundlinje·højde. En højde for af de to trekanter ΔABC og ΔACD er vist på tegningen nedenunder:

   

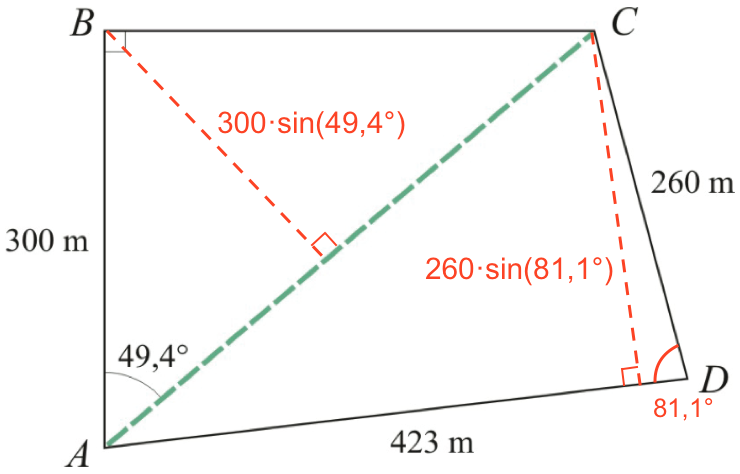
   I begge trekanter vælges grundlinjen |AC| = 461,0

   For ΔABC får man arealet: 0,5·461,0·300·sin(49,4°) m² = 52.502,4 m²

   For ΔACD får man arealet: 0,5·423·260·sin(81,1°) m² = 54.328,4 m²

   Dvs. ΔACD er størst

Svar på opgave 9:

1. Det er en lineær model y = ax + b, hvor y er samlet udgift til vandforbrug i kr. x er vandforbrug i kubikmeter, a er pris pr. kubikmeter i kr. og b er det faste årlige abonnement.

   Dvs. y = 34,15x + 581,25

2. Man skal løse ligningen 34,15x + 581,25 = 49,38x + 308,75 med hensyn til x. Man får følgende i Ti-Nspire:

   solve(34.15*x+581.25=49.38*x+308.75,x) ▸ x=17.8923

   Dvs. forbruget skal være 17,9 m³ om året før en forbruger i Holstebro skal betale mindre end en forbruger i Hillerød.

Svar på opgave 10:

1. Man opretter E(x) som funktion i Ti-Nspire:

   

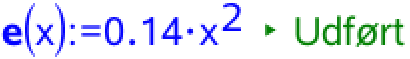
   Dernæst finder man E(50):

   

   Dvs. den årlige el-produktion for denne mølle er 350 kWh

   Man skal løse E(x) = 600:

   

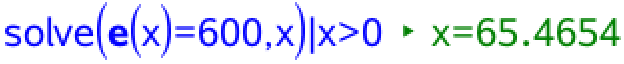
   Dvs. vingelængden for denne mølle er 65,5 cm

2. Man skal bruge procent-procent vækst formlen for potensfunktioner, idet fremskrivningsfaktoren for y (F_y) er 1 + 50 % = 1,50. Dvs. man skal beregne (F_y)^1/2 - 1 og omregne dette til %. Dette giver:

   

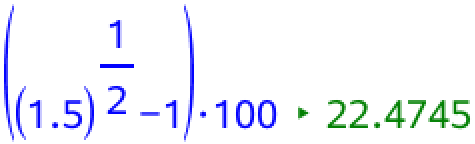
   Dette giver at denne mølle vinge er 22,5 % længere end den gamle.

Svar på opgave 11:

1. Man opretter f(x) i Ti-Nspire:

   

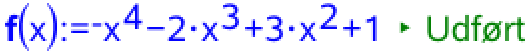
   Monotoniforholdene bestemmes ved at lave en fortegnsundersøgelse for f´(x). Dette gøres i Ti-Nspire som vist:

   

   

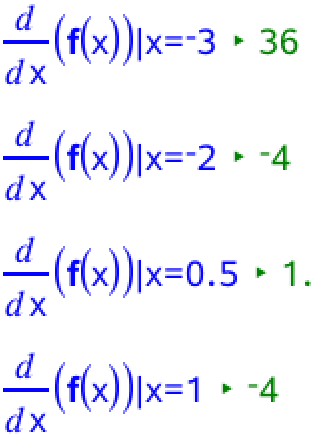
   Dvs. f´(x)>0 for x<-2,186; f´(x)<0 for -2,186<x>0; f´(x)>0 for 0<x>0,686 og f´(x)<0 for 0,686<x.

   Dermed er f voksende for x<-2,186,

   aftagende for -2,186<x<0,

   voksende for 0<x<0,686 og

   aftagende for 0,686<x

   Nedenfor er grafen tegnet i Ti-Nspire:

   

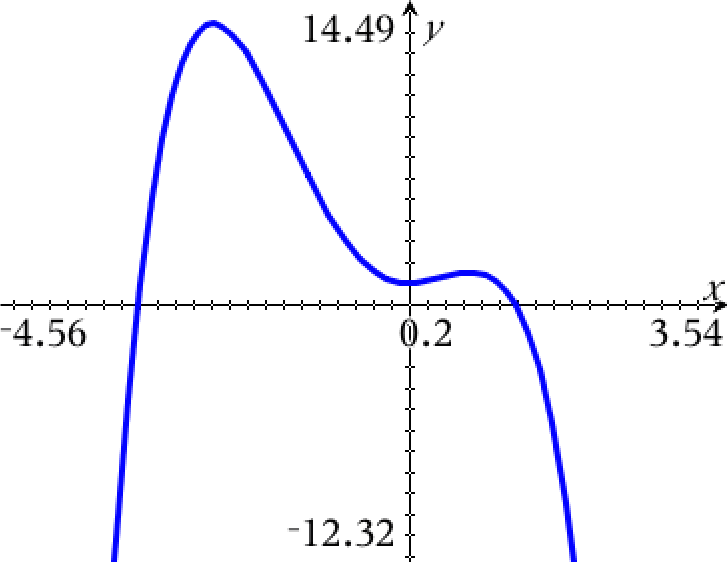
2. Man bruger kommandoen tangentLine() i Ti-Nspire til at finde tangentlinjen:

   

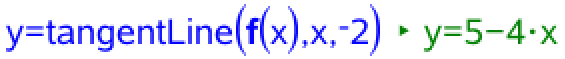
   En anden metode er:

   Formlen for tangenten gennem punktet (-2,f(-2)) er y = f´(-2)·(x - (-2)) + f(-2)

   Man finder i Ti-Nspire at f(-2) ▸ 13. Ovenfor har man fundet at f´(-2) = -4.

   y = f´(-2)·(x + 2) + f(-2) ⇒

   y = -4·(x + 2) + 13 ⇔

   y = -4·x - 8 + 13 ⇔

   y = -4·x + 5

   Dvs. ligningen for tangenten til f gennem punktet (-2,f(-2)) er y = -4x + 5

3. Man skal løse lignigen f(x) = -4·x + 5 med hensyn til x. Dette gøres i Ti-Nspire:

   

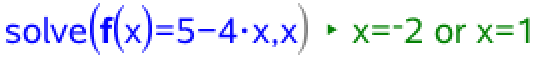
   Man får løsningerne x = -2 og x = 1. Den første løsning kender man allerede, så den anden er svaret på spørgsmålet. Man skal finde f(1) for at få y-værdien til røringspunktet: f(1) ▸ 1

   Dvs. punktet Q har koordinaterne (x,y) = (1,1)

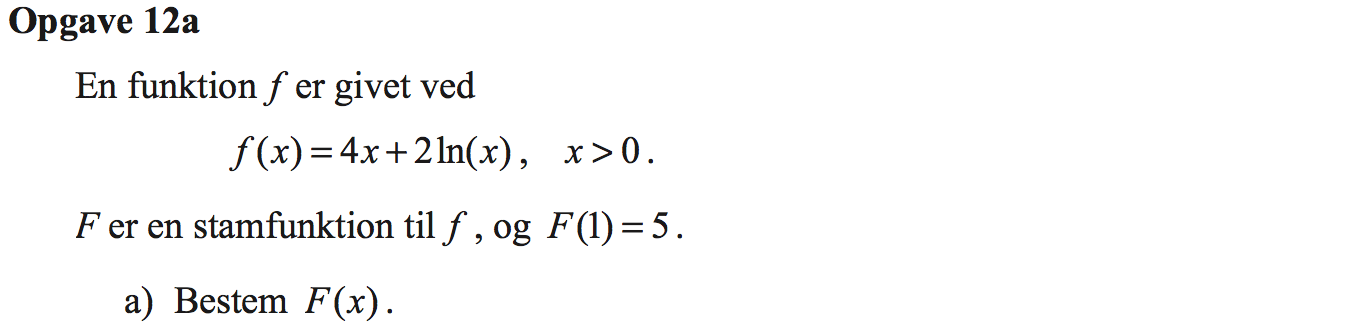
Svar på opgave 12a:

1. Man opretter f(x) i TI-Nspire:

   

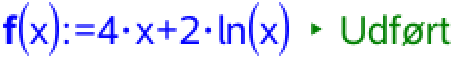
   Man bestemmer en stamfunktion til f(x) ved at finde det ubestemte integrale:

   

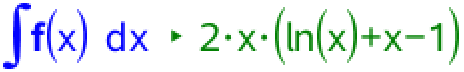
   Dermed er F(x) = 2·x·(ln(x) + x - 1) + k. Man skal bestemme k, så F(1) = 5. Det giver:

   

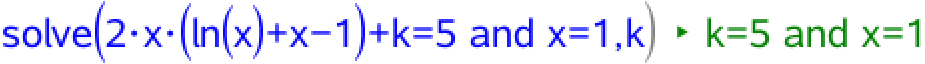
   Dvs. når værdien af k indsættes, får man F(x) = 2·x·(ln(x) + x - 1) + 5

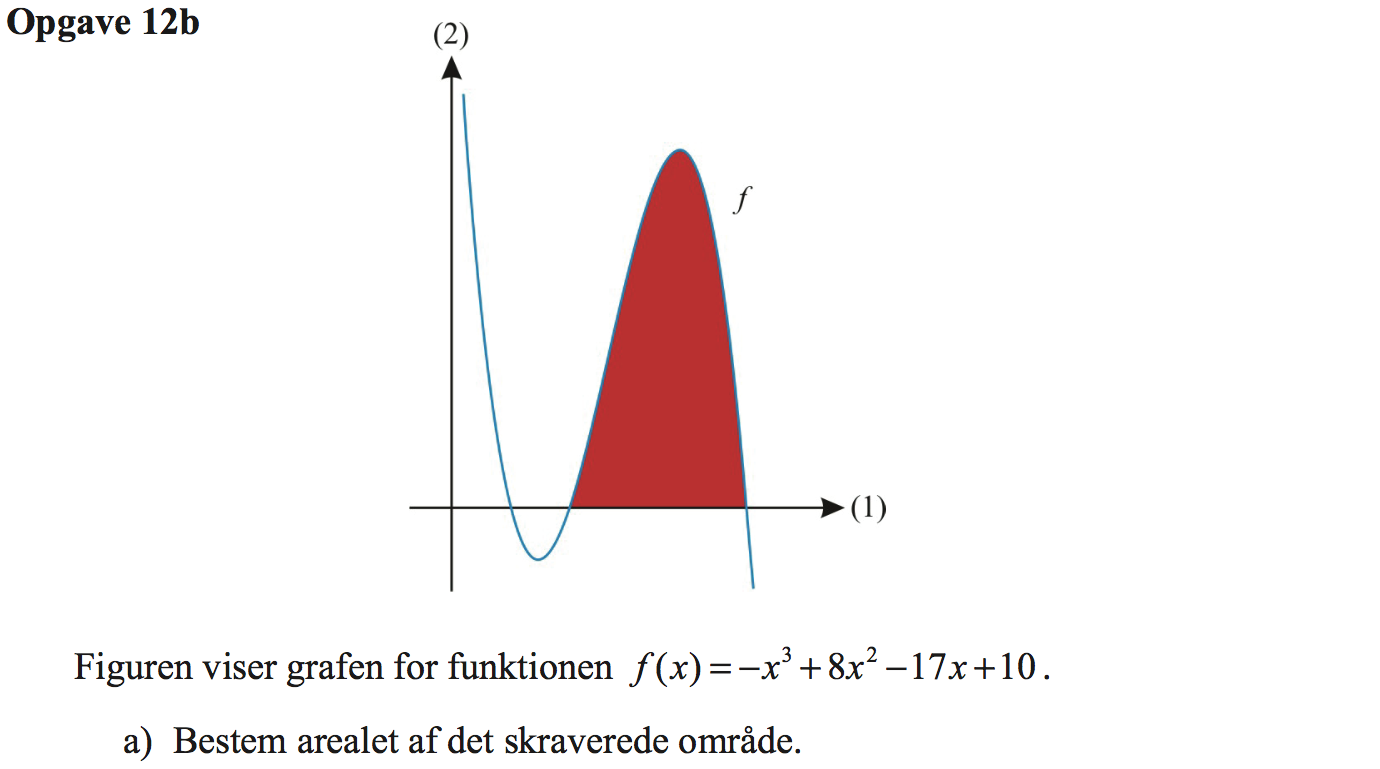
Svar på opgave 12b:

1. Man opretter f(x) i TI-Nspire:

   

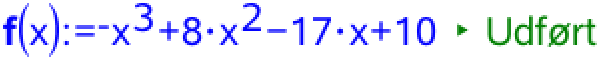
   Det røde område afgrænses på x-aksen af de to største af nulpunkterne for f. Disse nulpunkter bestemmes i Ti-Nspire:

   

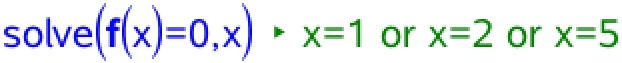
   Dvs. det røde område ligger mellem x = 2 og x = 5 og arealet af det råde område er derfor integralet af f mellem x = 2 og x = 5. Dette integrale er beregnet i Ti-NSpire:

   

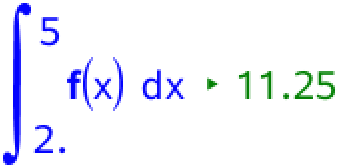
   Dvs. arealet af det røde område er 11,25