Svar på opgave 1: Togrejse i Europa

1. Prisforskellen er: 2830 kr. - 2200 kr. = 630 kr.
2. Pris efter rabat = (pris før rabat) - rabat =
   2830 kr. - (2830 kr.)·(15 %) =
   2830 kr. - (2830 kr.)·0,15 =
   2405,50 kr. ≈ 2400 kr.
3. Prisen for 20 overnatninger er:
   20·(pris pr. overnatning i €)·(€-kurs i kr.) =
   20·(22 €)·(743,56 kr./100 €) =
   20·22·743,56/100 kr. =
   3271,66 kr. ≈ 3270 kr.
4. Man indsætter først de tal, som man kender. Det er vist nedenunder. Se også Excel-fil.
   
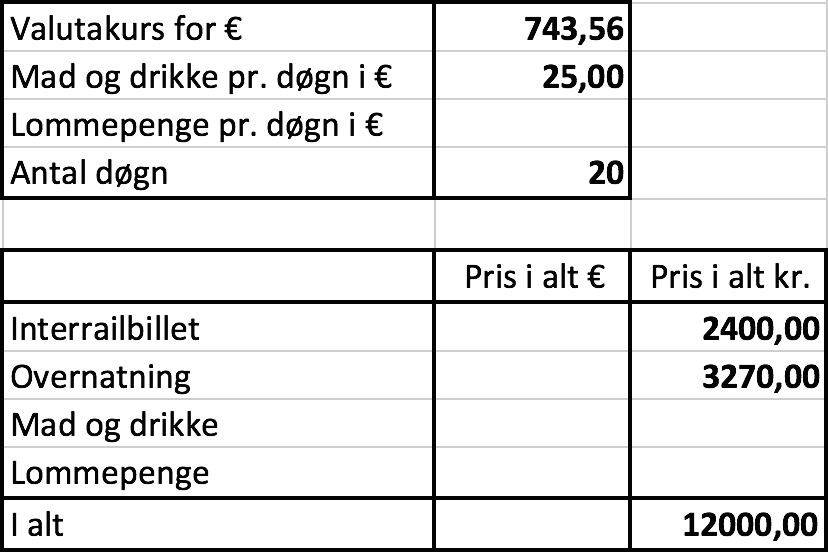
   Man beregner dernæst de samlede udgifter til mad og drikke - først i € og dernæst i kr.
   Det samlede beløb i € er (20 døgn)·(25 €/døgn) = 500 €.
   Dette regnes om til kr.: (500 €)·kurs = (500 €)·(743,56 kr./100 €) = 3717,80 kr.
   Lommepenge i kr. er: 12000,00 kr. - (2400,00 + 3270,00 + 3717,80) kr. = 2612,20 kr.
   Dette omregnes til €: 2612,20 kr./kurs = (2612,20 kr./(743,56 kr./100 €) = 351,31 €.
   Endelig udregnes den daglige udgift til lommepenge som samlet udgift til lommepenge i € divideret med antal døgn.
   Dette giver: (351,31 €)/(20 døgn) = 17,57 €/døgn.
   Dette tal rundes ned til 17,50 €/døgn for at være på den sikre side.

Svar på opgave 2: Første rejsedag

1. Man trækker rejsetid fra ankomsttidspunkt:
   8:31 - 0:45 =
   7:31 + 1:00 - 0:45 =
   7:31 + 0:15 =
   7:46
2. Man beregner rejsetiden ved at trække ankomsttidspunkt fra afgangstidspunkt:
   14:09 - 8:31 =
   6:09 - 0:31 =
   5:09 + 0:29 =
   5:38.
   Det vil sige, at rejsetiden er 5 timer og 38 min.
3. Rejsetiden i Danmark er 9:36 - 8:31 = 1:05 = (1 + 5/60) timer = 1,083 timer.
   Rejsetiden i Tyskland er 14:09 - 10:42 = 3:27 = (3 + 27/60) timer = 3,45 timer.
   Gennemsnitsfarten i Danmark er: (102 km)/(1,083 timer) = 94 km/t
   Gennemsnitsfarten i Tyskland er: (440 km)/(3,45 timer) = 128 km/t
   Det vil sige, at gennemsnitsfarten i Tyskland er størst.

Svar på opgave 3: Vinduer med rosettemønstre

1. Nedenfor er symmetriakserne tegnet i Geogebra. Der er 8
   
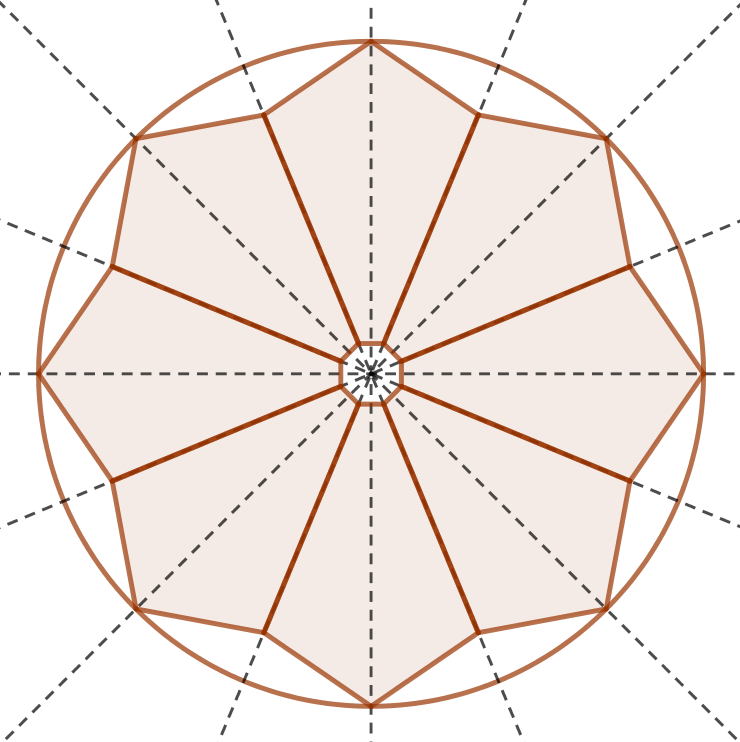
2. Nedenfor er vist en løsning fra Geogebra, hvor man kan flytte rundt på de tre blå punkter for at skabe rosettemønstre.
   
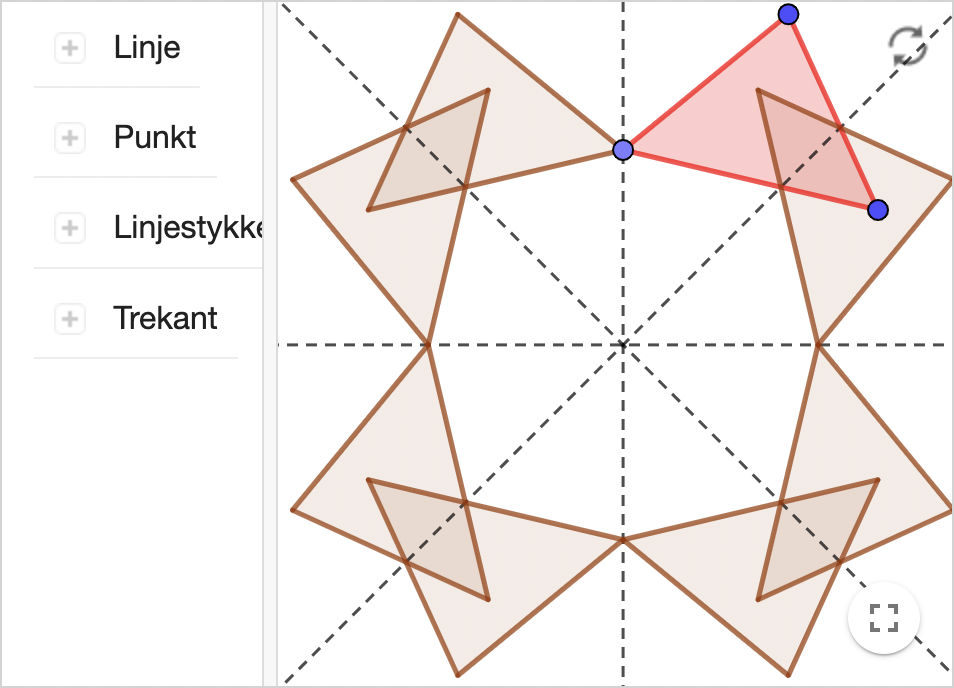
3. Den mindste drejningsvinkel er 120°, fordi hvis man drejer figuren 120° omkring cirklens centrum, så får man den samme figur, som man startede med.
4. Man bruger formlen og får antal drejninger til n = 360°/30° = 12
5. Der gælder, at n er alle de tal, som går op i 360. Disse findes i Geogebra ved hjælp af kommandoen DivisorListe(360):
   1,2,3,4,5,6,8,9,10,12,15,18,20,24,30,36,40,45,60,72,90,120,180,360

Svar på opgave 4: Indbyggertallet i Berlin

1. Forskellen i indbygger tal mellem 2011 og 2016 er: 3.580.531 - 3.292.365 = 288.166
2. Indekset for Berlins indbyggertal i 2016 er: (indeks for 2011)·(indbyggertal i 2016)/(indbyggertal i 2011) = 100·(3.580.531)/(3.292.365) = 108,8
3. Fra 2011 stiger kurven for Berlin hurtigere end kurven for København. Det vil sige, at den procentvise vækst i denne periode er størst for Berlin. Dernæst er det omvendt: den procentvise vækst for perioden 2012 - 2015 er større for København end for Berlin.
4. Man bruger fremskrivningsformlen: K = K₀·(1+r)ⁿ, hvor K er Berlins indbyggertal.
   Man skal se, om man K bliver ca. 3.580.531, når K₀ = 3.292.365, r = 1,7% = 0,017 og n = 2016 - 2011 = 5.
   Man får: K = 3.292.365·(1+0,017)⁵ = 3.292.365·(1,017)⁵ = 3.581.894.
   Afrundet til nærmeste 10.000 er dette det samme som det forventede og dermed er væksten i Berlins indbyggertal ca. 1,7 % om året fra 2011 til 2016.
5. Man antager, at der sker en forsat vækst i Berlins indbygger tal på 1,7 % fra 2016 til 2022. Dette er en periode på (2022 - 2011) år = 11 år.
   Man får samme formel som før, hvor n = 11, og får K = 3.292.365·(1,017)¹¹ = 3.963.131
   Det vil sige, at Berlins indbygger tal i 2022 forventes at være ca. 3.960.000

Svar på opgave 5: Rette linjer

1. At linjen m har et bestemt hældningstal betyder, at når x vokser med 1 så vokser y med hældningstallet. Det betyder i dette tilfælde, at når x vokser med 1 så vokser y med 1.
2. Ligningen for linjen m kan generelt skrives: y = a·x + b, hvor a er hældningstallet og b er linjens skæring med y-aksen. Denne aflæses til -2 som vist med rødt nedenfor. Det vil sige, at ligningen for linjen m er y = x - 2
3. Linjen n er tegnet nedenunder i Geogebra.
   
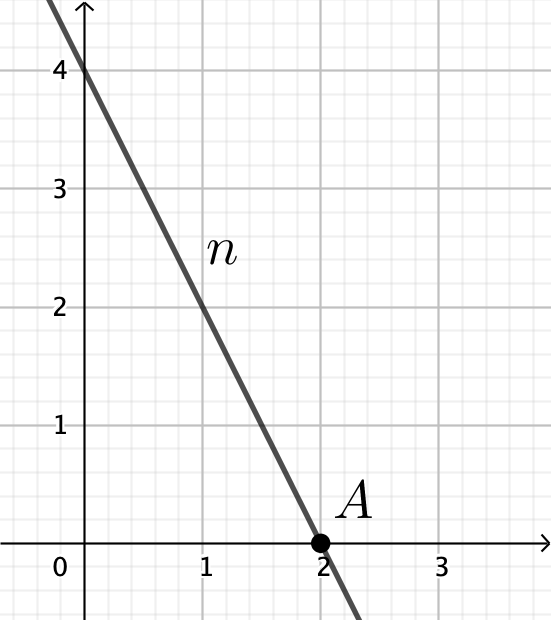
4. Nedenfor er vist røde linjer med hældningstal, a, der varierer fra -2 til 2. Deres skæring med y-aksen er også vist.
   
   Der gælder følgende sammenhæng:
   Hældningstal = -2, y-værdi af skæringspunkt: 4
   Hældningstal = -1, y-værdi af skæringspunkt: 2
   Hældningstal = 0, y-værdi af skæringspunkt: 0
   Hældningstal = 1, y-værdi af skæringspunkt: -2
   Hældningstal = 2, y-værdi af skæringspunkt: -4
   Det ses, at sammenhængen er: y-værdi af skæringspunkt = -2·(hældningstal)

Svar på opgave 6: Regneudtryk

1. Man får i det første tilfælde: 3 + 3/2 = 6/2 + 3/2 = 9/2 og i det andet: 3·(3/2) = 9/2
   Det vil sige, at de to regneudtryk har samme værdi.
2. I rækken med starttallet 10 skal der stå:
   10 + 10/9 i den første firkant og
   10·(10/9) i den anden.
3. I rækken med starttallet n skal der stå
   n + n/(n - 1) i den første firkant og
   n·n/(n - 1) i den anden.
4. Man kan ikke bruge starttallet n = 1, fordi nævneren i så fald bliver 0 i begge udtryk, og dette er ikke tilladt.
5. Det første regneudtryk kan skrives: n + n/(n - 1), og det andet: n²/(n - 1). De er ens, idet:
   n + n/(n - 1) =
   n·(n - 1)/(n - 1) + n/(n - 1) =
   (n² - n + n)/(n - 1) =
   n²/(n - 1)