Svar på opgave 1: Biler og udledning af CO₂

1. Bilen udleder: (153 km)·(140 g CO₂/km) = 21,4 kg CO₂
2. Den procentvise nedgang i CO₂-udledning, når man går fra den gamle bil til den nye, er: [(140 - 88)/140]·100 % = 37,1 %
3. Det antal km, som den nye bil må køre for højst at udlede 1,7 tons CO₂, kaldes x. Der gælder:
   x·(88 g CO₂/km) = 1,7 tons CO₂ ⇔
   x = (1,7 tons CO₂)/(88 g CO₂/km) ⇔
   x = (1,7·1.000.000 g)/(88 g) km ⇔
   x = 19.318 km.
   Det vil sige, at Klaus skal køre ca. 19.300 km på et år for at udlede 1,7 tons CO₂.
4. Nedenfor er grafen tegnet i Geogebra.
   
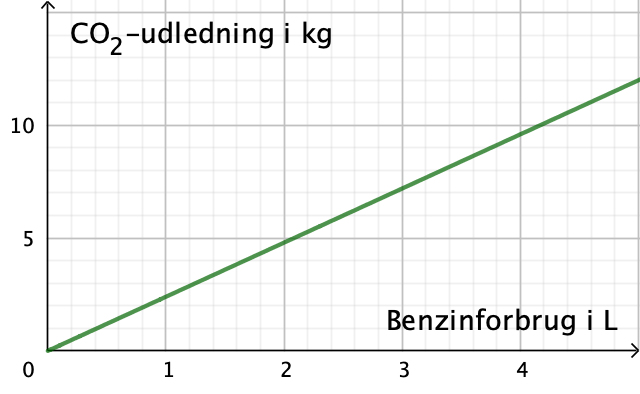
5. Antallet af km, som bilen kører på en liter benzin, kaldes x. Man får: x·(0,088 kg CO₂/km) = 2,4 kg CO₂ ⇔ x = 2,4/0,088 km = 27,27 km
   Det vil sige, at Klaus' bil kører 27,3 km pr. liter benzin
6. Den masse af CO₂, som han udleder, er: (15.000 km)·(0,088 kg/km) = 1320 kg. Rumfanget er: (1320 kg)/(1,8 kg/m³) = 1320/1,8 m³ ≈ 730 m³
7. Ballonen er en kugle og har rumfanget: (4/3)·π·r³. Man har følgende ligning for r:
   (4/3)·π·r³ = 730 m³ ⇔
   r³ = 3·730/(4·π) m³ ⇔
   r = ³√[3·730/(4·π)] m = 5,5857 m
   Det vil sige, at ballonens radius er 5,6 m

Svar på opgave 2: Menneskeskabt udledning af CO₂

1. Udledningerne aflæses af grafen. Forskellen mellem 1950 og 2013 var: (36.234 - 5976) mio. tons CO₂ = 30.258 mio. tons CO₂
2. Den procentvise forskel mellem 2000 og 2013 var: ((36.234 - 24.805)/24805)·100 % = 46,1 %
3. Tallet 450 i den første model er den årlige vækst i mio. tons. Tallet 0,03 i den anden model er den årlige vækstrate i udslip af CO₂.
4. Nedenfor er de to modeller indsat i et diagram sammen med søjler for CO₂-udslip. De to modeller ses at passe omtrent lige godt med søjlerne.
   
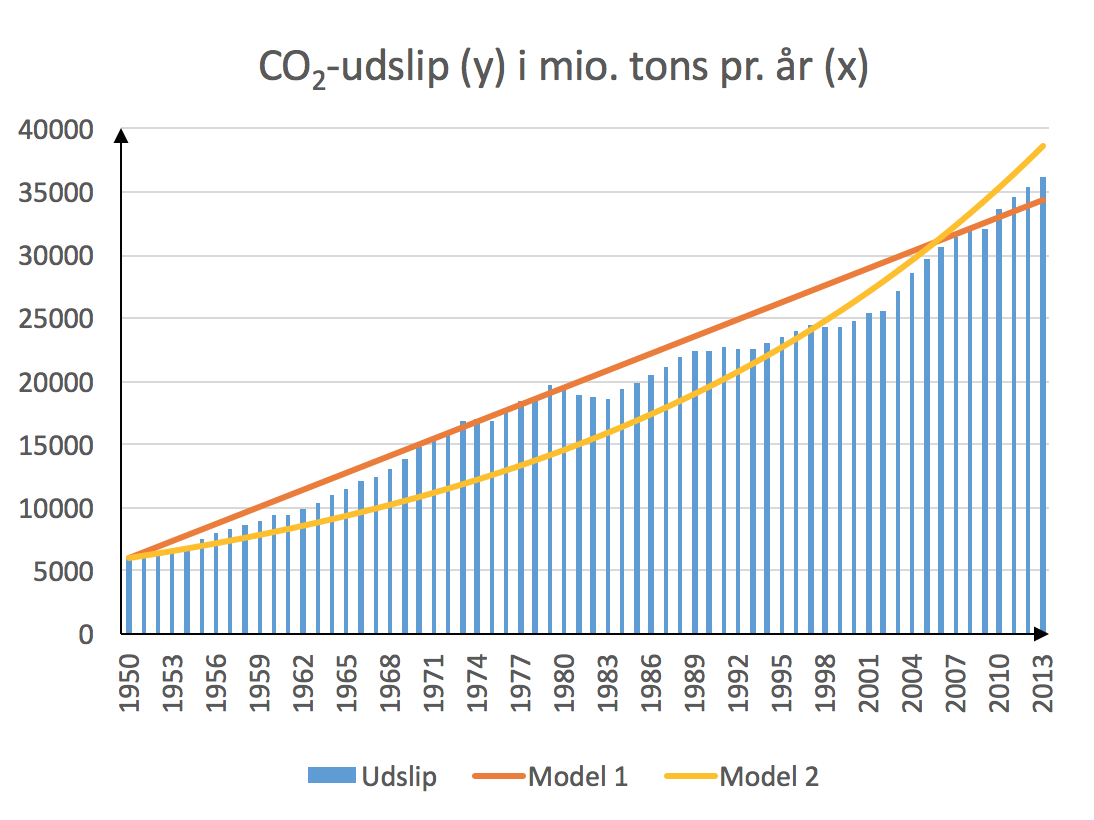
5. Antal år = 2050 - 1950 = 100.
   Forudsigelse med model 1: 6000 + 450·100 = 51.000.
   Forudsigelse med model 2: 6000·1,03¹⁰⁰ = 115.312.
   Forskellen er: (115.312 - 51.000) mio. tons CO₂ = 64.312 mio. tons CO₂.
6. De to diagrammer ser forskellige ud, fordi man i det nederste diagram forstørrer y-aksen op i det område, hvor kurverne ligger. Samtidig er den blå y-akse forskudt nedad i forhold til den røde, så de to kruver falder sammen.

Svar på opgave 3: Vasketøj og udledning af CO₂

1. De 3 vaske, der er på 40 °C, udleder: 3·0,8 kg CO₂ = 2,4 kg CO₂.
   Den ene vask, der er på 60 °C, udleder: 1,1 kg CO₂.
   Pr. vask udleder familien: (2,4 + 1,1)/4 kg CO₂ = 0,875 kg CO₂
2. Udledningen af CO₂ pr. kg tøj er: 1,1/x kg CO₂, hvor x er tøjets vægt i kg.
3. Hældningen af kurven er 0,6/40 kg = 0,015 kg. Det vil sige, at når man mindsker vaske-temperaturen med x °C, så bliver CO₂-besvarelsen 0,015·x kg CO₂.
4. Antallet af vaske om ugen er i gennemsnit (4/6)·4 = 2,67. Det er 0,67 vaske ved 60° og 2 ved 20°.
   Udslip: 0,67·1,1 + 2·(0,8 - 20·0,015) kg CO₂ = 1,74 kg CO₂.
   I øjeblikket udleder familien 3,5 kg CO₂ om ugen, der er ca. det dobbelte af 1,74. Det vil sige, at Klaus har ret.

Svar på opgave 4: En ligebenet, retvinklet trekant

1. ΔABC er retvinklet, fordi den deler et hjørne med kvadratet. Den er ligebenet, fordi den deler to sider med kvadratet.
2. Nedenunder er tegnet en retvinklet ligebenet trekant i Geogebra.
   
3. På tegningen nedenunder er vist ΔADO, der indeholder v, og hvor D er det sted, at vinkelhalveringslinjen fra B skærer AC. Denne linje er samtidig højde i B, da B er toppunkt i en ligebenet trekant. Dermed er ∠ODC 90°. ∠OAD er 45°/2 = 22,5°. Vinkelsummen i ΔADO er 180°, så v = 180° - 90° - 22,5° = 67,5°
   
4. |AB| = |BC| = 10. Da |AC| er hypotenusen i en retvinklet ligebent trekant, så er |AC| = √2·|AB| = 14,142. Omkredsen er: 2·10 + 14,142 ≈ 34,14
5. T = (1/2)·katete² = (1/2)·10² = 50, og s = 34,14/2 = 17,07. Dette giver: radius = 50/17,07 = 2,93

Svar på opgave 5: Regneruter

1. I den øvre rute får man regnestykkerne: 10 + 3 = 13 og 13·2 = 26
   I den nedre rute får man: 10·2 = 20 og 20 + 3 = 23
2. I den første firkant indsætter man x, som findes af den øvre rute: x (x + 3)·2 = 2 ⇔ x + 3 = 2/2 ⇔ x = 2/2 - 3 = 1 - 3 = -2. Det vil sige, at starttallet er -2
3. Man undersøger hvilke starttal, der giver et sluttal på 100 for de to veje.
   Øvre rute: (x + 3)·2 = 100 ⇒ x = 47.
   Nedre rute: x·2 + 3 = 100 ⇒ x = 97/2 = 48,5.
   Det ses, at vælger man 48 som starttal, så vil øvre rute give 102, mens nedre rute vil give 99, så 48 opfylder betingelsen.
4. Man indsætter -2/3 som starttal:
   Øvre rute: (-2/3 + 3)·2 = 14/3
   Nedre rute: (-2/3)·2 + 3 = 5/3
   Forkellen er 14/3 - 5/3 = 3. Dermed tager Stine fejl
5. Man indsætter x som starttal og får: øvre rute: (x + 3)·2 = 2·x + 6. Nedre rute: x·2 + 3 = 2·x + 3.
   Forskellen på øvre og nedre rute er: 2·x + 6 - (2·x + 3) = 3.
   Dette viser, at uanset hvilket starttal, som man vælger, så får man altid en forskel på 3. Dermed har Klaus ret.