Svar på opgave 1: Kørekort

1. Prisen er (1899 + 1899 + 2199 + 600 + 16·350) kr. = 12.197 kr.
2. Hun sparer: ((12.197 - 10.999)/12.197)·100 % = 9,8 % ved at vælge køreskole 2 frem for køreskole 1.
3. Hun skal betale: 10.999 kr. + 2·475 kr. = 11.949 kr. for køreskole 2, hvis hun tager 2 lektioner ekstra ud over de 16.
4. Prisen for køreskole 2 er: (10.999 + (n - 16)·475) kr. = (475·n + 3399) kr. hvor n er antal kørelektioner.
5. Prisen for Køreskole 1 er: (350·n + 6597) kr. Man finder det n, der gør de to køreskoler lige dyre:
   350·n + 6597 = 475·n + 3399 ⇔
   n = (6597 - 3399)/(475 - 350) ⇔
   n = 25,6
   Det vil sige, at Marie højst må tage 25 kørelektioner for at Køreskole 2 er billigst.

Svar på opgave 2: Bilsalg

1. Det gennemsnitlige antal solgte luksusbiler pr. år fra 2010 til 2015 er: (111 + 158 + 116 + 125 + 148 + 136)/6 = 132,3 = 132
2. Mellemstore bilers procentdel af det samlede bilsalg:
   2010: (32804/153902)·100 % = 21,3 %
   2015: (44804/207552)·100 % = 21,6 %
   Det vil sige, at hun har ret i sin påstand inden for en forskel på 0,3 % point.
3. Nedenstående kurve er lavet i Excel. Det ses, at salget af mikrobiler stiger fra 2010 til 2013 for derefter at falde igen. Overordnet stiger salget fra 2010 til 2015.
   
4. Procentvis fald i salg:
   Sportsvogne: ((230 - 143)/230)·100 % = 37,8 %
   Store familiebiler: ((22.081 - 19.287)/22.081)·100 % = 12,7 %
   MPV'er: ((16577 - 11.099)/16.577)·100 % = 33,0 %
   Det vil sige, at salget af sportsvogne har det største procentvise fald.
5. Den gennemsnitlige årlige stigning i salget af biler fra 2010 til 2015 er (207.552 - 153.902)/6 = 8941,7. Hvis denne stigning fortsætter indtil år 2020, så får man følgende salgstal: 207.552 + 5·8941,7 = 252.000

Svar på opgave 3: Nummerplader med palindromtal

1. Et eksempel på et 5-cifret palindromtal med 2 som første ciffer er 21012
2. Der er 10 muligheder: 73037, 73137, 73237, 73337, 73437, 73537, 73637, 73737, 73837 og 73937
3. Man skal vælge 3 cifre: Det første det andet og det tredje. Det fjerde og det femte følger af de to første.
   For det første ciffer er der 9 muligheder, nemlig tallene fra 1 til 9. Cifferet 0 kan ikke vælges, da tallet i så fald kun vil være fire-cifret.
   Det andet og tredje ciffer kan vælges mellem alle cifre fra 0 til 9. Det vil sige, at der er 10 muligheder for hver.
   Dette giver i alt: 9·10·10 = 900 mulige femcifrede palindromtal.
4. Sandsynligheden for, at man tilfældigt ser en bil med et palindromtal på nummerpladen, er: antal femcifrede palindromtal (900) divideret med antal femcifrede tal. I et femcifret tal kan det første vælges mellem 9 cifre og de fire andre mellem alle 10 cifre. Dette giver: 9·10·10·10·10 = 90.000 femcifrede tal. Sandsynligheden for at møde en bil med et palindromtal er derfor 900/90.000 = 0,01, og sandsynligheden for at møde to i træk er: 0,01·0,01 = 0,0001 = 0,01 %

Svar på opgave 4: Figurfølger

1. Fígur 5 er tegnet nedenunder i Geogebra.
   
2. Det bemærkes, at for at komme fra en figur til den næste, skal man lægge 3, 5, 7, 9...firkanter til.

   Figur	1	2	3	4	5	6	7	8	9
   Antal kvadrater	2	5	10	17	26	37	50	65	82

3. Figur 12 indeholder: 82 + 19 + 21 + 23 = 145 firkanter.
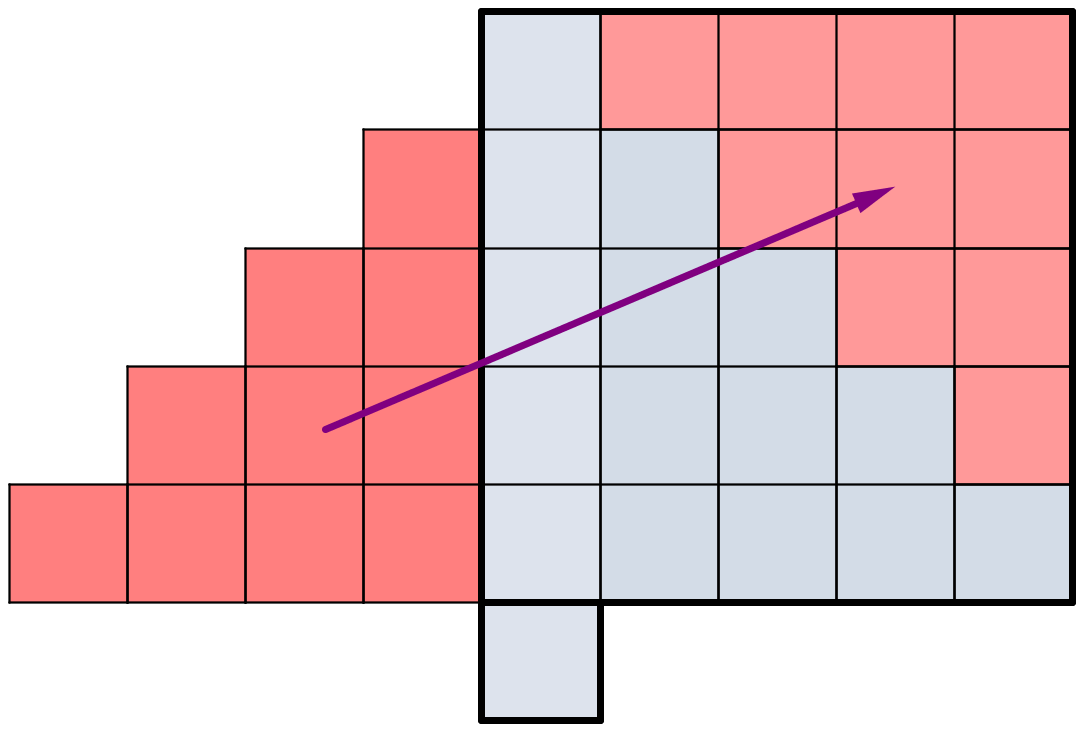
4. Nedenstående figur viser, hvordan man kan omarrangere firkanterne i en figur, så der dannes et stort og et lille kvadrat, som begge er indrammet med fed streg. Det store kvadrat indeholder n² små kvadrater, hvor n er nummeret på figuren i figurfølgen. Det vil sige, at figur n i figurfølgen indeholder: n² + 1 små kvadrater.
   
5. Antallet af kvadrater i figur 100 er 100·(100 + 1) = 100·101 = 10.100
6. Man skal løse ligningen:
   n·(n + 1) = 1122 ⇔
   n² + n - 1122 = 0 ⇔
   n = -½ ± ½·√[4489] ⇔
   n = -34 (ugyldig) ∨ n = 33
   Det vil sige, at nummeret for figuren er 33

Svar på opgave 5: Firkant i kvadrat

1. Nedenstående tegning er lavet i Geogebra.
   
2. Trekant AEH er en retvinklet trekant med kateterne 4 og (10 - 4) = 6. Dens areal er 0,5·4·6 = 12
3. HE og EF er hver især hypotenuse i en retvinklet trekant med kateterne 4 og 10. Da kateterne er ens, er hypotenuserne det også.
4. Trekanterne AEH og BEF er retvinklede og kongruente. Dermed er u₁ + v₂ = 90°. Det ses, at: w + (u₁ + v₂) = 180° ⇒ w = 180° - 90° = 90°
5. Den variable x er afstanden fra A til E, der ligger på AB. Dermed er x større end eller lig med 0 og mindre end eller lig med 10.
6. Nedenstående graf for f(x) er tegnet i Geogebra.
   
7. Man skal finde x i ligningen:
   2x² - 20x + 100 = 68 ⇔
   2x² - 20x + 32 = 0 ⇔
   x = 5 ± ¼·√[144] ⇔
   x = 2 ∨ x = 8
   Det vil sige, at når arealet af EFGH er 68, kan x have værdierne 2 eller 8
8. Ved at betragte kurven for arealet af EFGH ses, at den mindste værdi findes for x = 5, der giver arealet 50