Folkeskolens problemregning for 10. klasse, maj 2016 · Opgavesæt | Gå til oversigt

Svar på opgave 1: Mads undersøger priser i et fitnesscenter

  1. Forskellen på oprettelse af medlemskab for voksne og for unge under 18 år er: (249 - 99) kr. = 150 kr.
  2. Han skal betale: 99 kr. + 6·165 kr. = 1089 kr.
  3. Formlen for de første n måneder er 99 + n·165 kr.
  4. For familliemedlemskab får man prisen: (399 + n·599) kr. For enkeltmedlemskaber får man: 99 + n·165 + 2·(249 + n·169) = (597 + n·503) kr.
    Man sætter de to pris-udtryk lig med hinanden og løser med hensyn til n:
    399 + n·599 = 597 + n·503 ⇔
    n = (597 - 399)/(599 - 503) ⇔
    n = 2,0625
    Det vil sige, at familiemedlemskab er billigst de to første måneder, hvorefter enkeltperson-medlemskab er billigst.

Svar på opgave 2: Helene undersøger tal fra en skydeprøve

  1. Man lægger tallene sammen i kolonnen med overskriften Antal tilmeldte, der ikke deltog i prøven. Det giver, at: 1 + 1 + 1 + 1 + 1 = 5 personer ikke deltog.
  2. Beståelsesprocenten beregnes som [(antal beståede)/(antal tilmeldte)]·100 % = (7/11)·100 % = 63,6 %.
  3. Beståelsesprocent = [(antal beståede)/(antal tilmeldte)]·100 %. Antal tilmeldte = 109, antal beståede = x og beståelsesprocenten = 73,8 %. Man får ligningen:
    73,8 % = (x/109)·100 % ⇔
    x = (73,8 %)/(100 %)·109 ⇔
    x = 80,44
    Det vil sige, at der skulle have været 80 personer, som bestod prøven, for at beståelsesprocenten havde være det den samme begge steder.
  4. Helene har ret. Man skal tage det samlede antal personer, der bestod og dividere med det antal, der var tilmeldt.
    Helenes regnestykke: [(7 + 11 + 27 + 13 + 31 + 45 + 37 + 36 + 42 + 52)/(11 + 15 + 43 + 20 + 49 + 61 + 71 + 61 + 82 + 109)]·100 % = (301/522)·100 % ≈ 58 %.
    Farens regnestykke: (63,6 % + 73,3 % + 62,8 % + 65,0 % + 63,3 % + 73,8 % + 52,1 % + 59,0 % + 51,2 % + 47,7 %)/10 ≈ 61 %.
    Fejlen for Helenes far er, at skydebanerne ikke har lige mange deltagere, så deres procenttal kan ikke lægges sammen.

Svar på opgave 3: Allan cykler på bane

  1. Omkredsen af den blå linje = 2·46,00 m + 2·π·25,15 m = 250,0 m
  2. 4000 m svarer til (4000 m)/(250 m) = 16 omgange
  3. Allans tid = strækning/gennemsnitsfart = (4.000 m)/(11 m/s) = 363,6 s ≈ 6 min. 4 s
  4. I følge formlen får man t = [125/(11 - 10,5)] s = (125/0,5) s = 250 s
  5. Allan har kørt i 250 sekunder med en gennemsnitsfart af 11 m/s. Dermed er den tilbagelagte vej: (250 s)·(11 m/s) = 2750 m
  6. Allans tid er 5 min. 12 s = 312 s og hans distance er lig med Bo's plus en halv baneomgang = 3455 m + 125 m = 3580 m.
    Dette giver: Allans gennemsnitsfart = (3580 m)/(312 s) = 11,5 m/s

Svar på opgave 4: Rasmus og Sonja spiller et terningespil

  1. De mulige udfald af øjne er (1,6), (2,5), (3,4), (4,3), (5,2), (6,1)
  2. Der er een mulighed ud af 36 for at få to enere, det vil sige, at sandsynligheden er 1/36 = 2,8 %
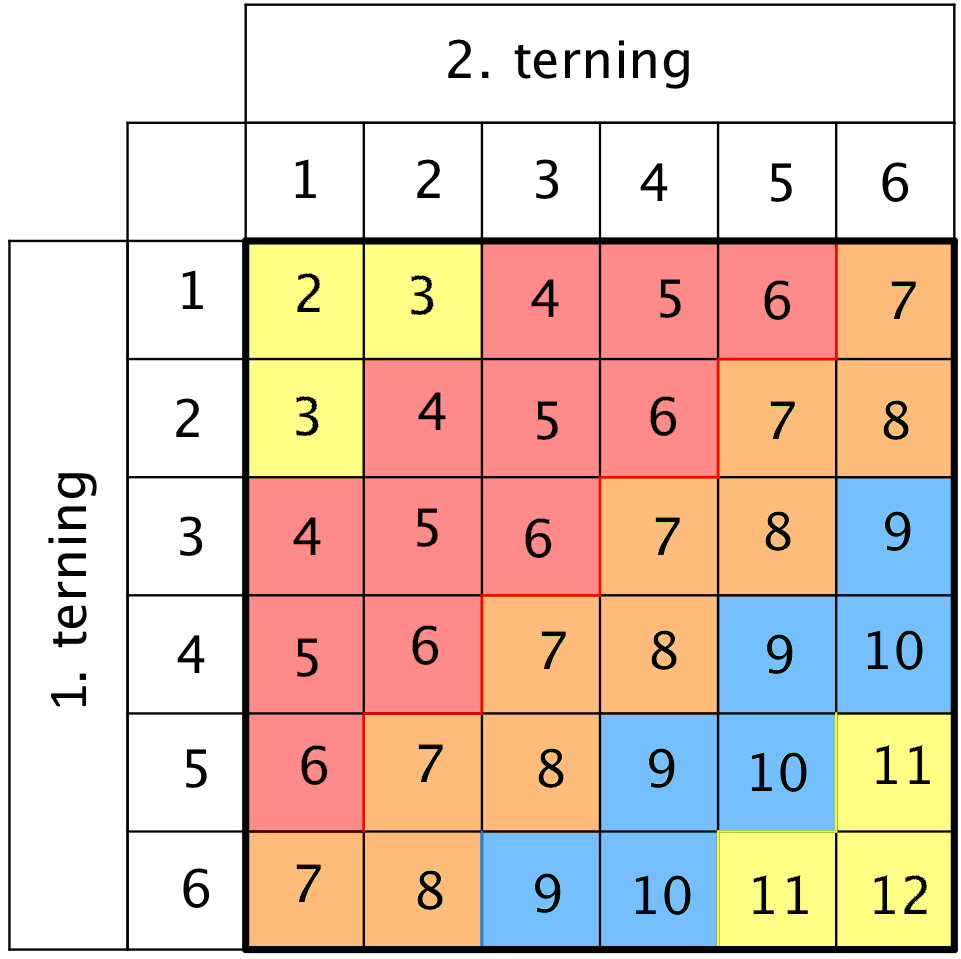
  3. Nedenfor er vist en tabel over summen af øjne for de to terninger. Hver tern med en bestemt farve svarer til en gevinstmulighed for feltet med samme farve på spillefladen. Der er 36 tern i alt. Det vil sige, at sandsynligheden for at få en sum af øjne på det...
    ...gule felt er 6/36 = 1/6 = 16,7%,
    ...røde felt er 12/36 = 1/3 = 33,3 %,
    ...orange felt er 11/36 = 30,6 % og
    ...blå felt er 7/36 = 19,4 %.
    Dermed har Rasmus ikke ret. Sandsynligheden for at vinde er størst på det røde felt.

Svar på opgave 5: Rasmus tegner en mandorla

  1. Nedenstående tegning er lavet i Geogebra.
  2. De fire sider er alle radier i ens cirkler. Dermed er de lige lange.
  3. Nedenunder er en tegning, hvor de to centre er forbundet. Det ses, at firkant AC1BC2 består af to ens ligesidede trekanter, hvor sidelængden er lig med radius i cirklerne. Dermed er alle vinkler i trekanterne 60°. Da vinkel C1 og vinkel C2 består af to vinkler på 60°, så er de 120° hver.
  4. Hver af mandorlaens sider er en sjettedel af omkredsen af en cirkel med radius 10 = (1/6)·2·π·10 = (20/3)·π. Dermed er hele omkredsen: 2·(20/3)·π = (40/3)·π = 41,9
  5. Arealet af mandorlaen er [(4π - 3√3)/6]·102 = 122,8
  6. Man kalder krydsningspunktet for diagonalerne for D. Det ses at ΔAC2D er en retvinklet trekant med vinklerne 30°, 60° og 90°,da den halverer en ligesidet trekant. Hypotenusen lig med 10. Den længste katete er 10·(√3/2). Dermed er den længste diagonal = 10·√3 = 17,3
  7. Man har som ovenfor, at halvdelen af længste diagonal er (√3/2)·r. Dermed er den længste diagonal r·√3.

Svar på opgave 6: Sonja tegner sekskanter

  1. Som vist nedenunder, så kan sekskanten inddeles i et rektangel (A) og et kvadrat (B). Dermed er arealet af sekskanten 7·2 + 3·3 = 14 + 9 = 23
  2. Sekskanten inddeles igen i et rektangel (A) og et kvadrat (B). Dette er vist nedenunder. Kvadratet har siden √5. Dermed er arealet af sekskanten (4·√5)·(2·√5) + (√5)·(√5) = 8·5 + 5 = 45
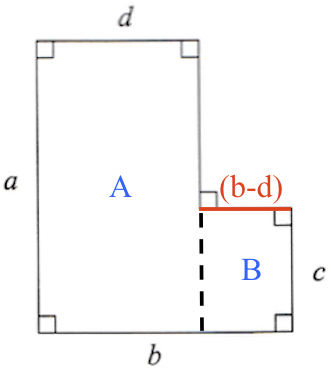
  3. Sekskanten inddeles i to rektangler: A med siderne a og d, B med siderne (b-d) og c. Arealet af sekskanten = a·d + (b-d)·c = a·d + b·c - c·d. Man undersøger nu, hvilke udtryk som ikke kan omskrives til dette:
    1. c·(b-d) + a·d = a·d + b·c - c·d
    2. a·b - (a - c)·(b - d) = a·b - a·b + a·d + b·c - c·d = a·d + b·c - c·d
    3. a·b - c·(b - d) = a·b - b·c + c·d
    4. d·(a - c) + b·c = a·d + b·c - c·d
    Formel 3 ses at være forkert.
  4. Omskrivning:
    d·(a - c) + c·(b - d) + c·d =
    d·a - d·c + c·b - c·d + c·d =
    a·d - c·d + b·c