Svar på opgave 1: Kan Charlotte få råd til at bo i lejlighed?

1. Hun skal betale: 1939 kr. + 265 kr. = 2204 kr.
2. Hun skal i gennemsnit betale: 400 kr. + 198 kr. + (1218/6) kr. + (4000/12) kr. + (1800/12) kr. = 1284,33 kr.
3. Hun får udbetalt: 3816 kr. + (5839 - 3816)·(100% - 37%) kr. = 3816 kr. + 1274.49 kr. = 5090,49 kr.
4. Hun får udbetalt: 3000·(100% - 8%)·(100% - 37%) kr. = 3000·0,92·0,63 kr. = 1738,80 kr.
5. Det beløb, som hun skal tjene er: (1500 kr.)/(0,92·0,37) = 2588 kr.

Svar på opgave 2: Patienter med forbrændinger

1. Man skal finde V i Parklands formel. V = 4·m·A·100 mL = 4·63·0,25·100 mL = 6300 mL
2. Patienten får: 3150 mL/(8 timer) = 3150 mL/(8·60 min.) = 3150/480 mL/minut = 6,56 mL/min.
3. Man skal finde A i Parklands formel: 10.000 = 4·85·A·100 ⇔ A = 10.000/(4·85·100) = 29,4 %
4. Væske pr. tidsenhed: 8 mL/min. = 8 mL/(1/60 time) = 8·60 mL/time = 480 mL/time
5. Tiden kaldes x:
   x·480 mL/time = 1.000 mL ⇔
   x = 1000/480 timer = 2 1/12 time = 2 timer og 5 min.
6. Da den tredje patient får 8 mL væke i minuttet, så giver det forskriften: y = 8·x, hvor x er antal minutter og y er antal mL væske.

Svar på opgave 3: Antal personer indlagt på hospitaler i Danmark

1. Summen er 26.771 + 21.155 + 19.192 + 45.334 + 56.915 + 36.921 + 37.525 + 47.316 + 46.509 + 49.680 = 387.318
2. Søjlediagram i Excel. Første-aksen er alder.
   
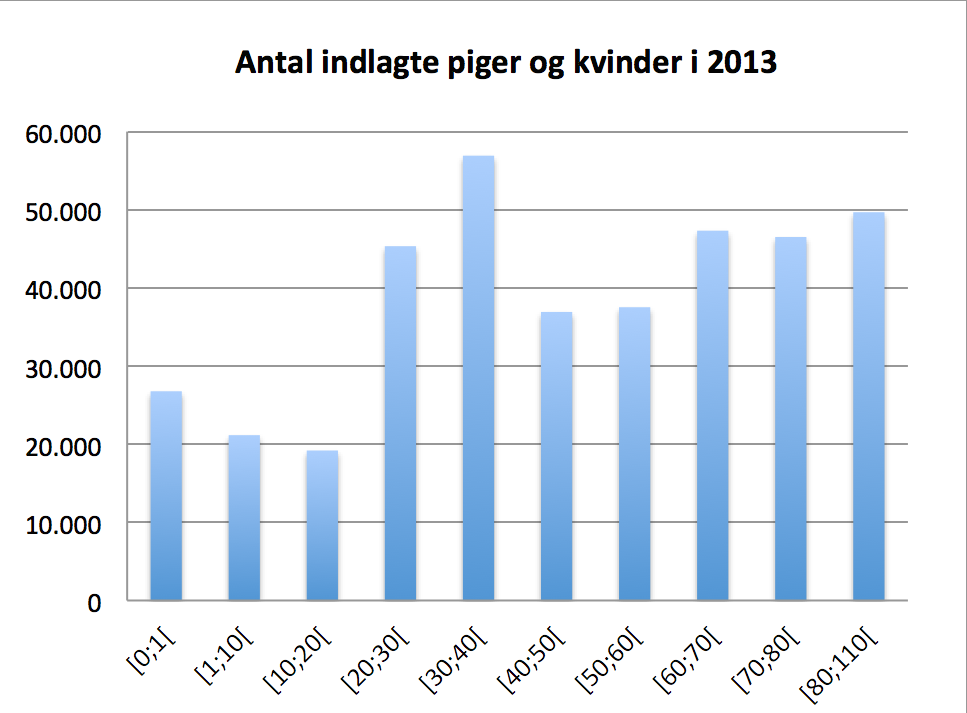
3. Sandsynligheden er antal indlagte divideret med antal personer for aldersgruppen. For mænd mellem 80 og 110 bliver det: 33448/86570 = 0,386 og for kvinder: 49680/147749 = 0,336. Dette viser at Charlotte har ret.
4. Det gennemsnitlige antal indlæggelsesdage for en person er den blå søljes højde divideret med den rødes i 2013. Dette giver: (4.300.000 dage·personer)/(700.000 personer) = 6,1 dage.
5. Det gennemsnitlige antal sengedage er faldet fra ca. 5/0,7 = 7 i 2006 til ca. 6 i 2013.

Svar på opgave 4: Figurfølger

1. Tegning af figur 4.
   
2. I figur nr. 5 er der 49 felter, da nederste række består af kvadrattal, og 49 er det næste.
3. Man sætter n = 10 i formlen for skraverede felter og får: 100·(100 + 2) = 100·102 = 10.200
4. Man reducerer udtrykket: 2 + 2·(n + 1) + n·(n + 2) = 2 + 2n + 2 ² + 2n = n² + 4n + 4
5. Hun har ret idet: (n + 2)² = (n + 2)·(n + 2) = n² + 4n + 4

Svar på opgave 5: Diofantiske trekanter

1. Trekant med siderne 8 cm, 6 cm og 5 cm
   
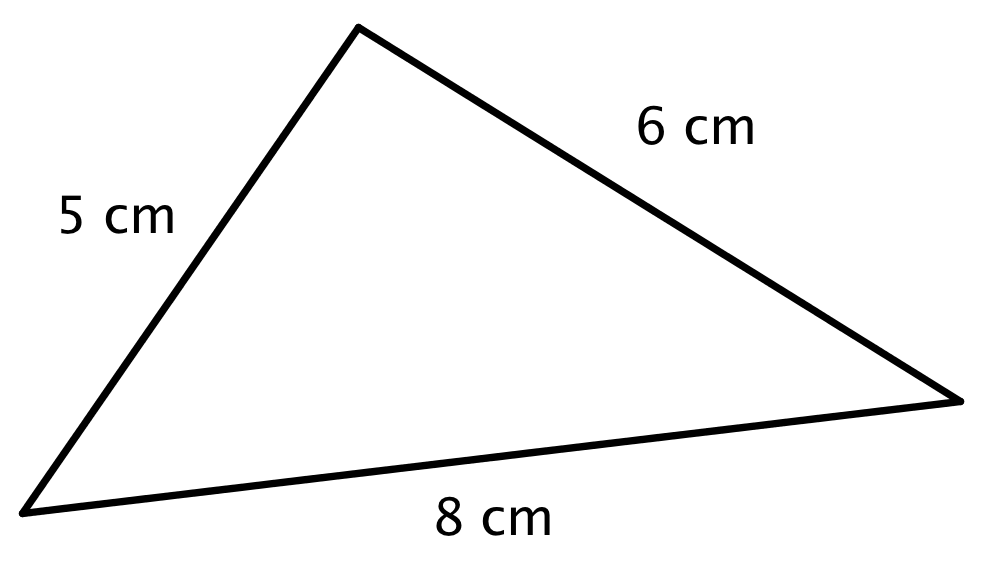
2. Trekant 2 er retvinklet fordi sidelængderne er en Pythagoræisk triplet. Det gælder ikke for de andre.
3. Den ligesidede trekant har det største areal, fordi de alle har samme omkreds, og en ligesidet trekant er den trekant, som har det største areal i forhold til sin omkreds.
4. Den kan højst være 7 cm. Summen af længderne af de to mindste sider er større end længden af den største. Dermed er den længste side mindre end halvdelen af omkredsen og dermed højst 7 cm, når den skal være et helt tal.
5. Der er 7 muligheder: 7-7-1, 7-6-2, 7-5-3, 7-4-4, 6-6-3, 6-5-4 og 5-5-4.
6. Som nævnt i spørgsmål 4, så er den længste side mindre end halvdelen af omkredsen, der er p/2. Dette viser, at Charlotte har ret, hvis hun mener: Det største hele tal som er mindre end eller lig med (p - 1)/2.