Svar på opgave 1: Huspriser

1. Af kurven aflæses, at den højeste pris var i 2008.
2. Gennemsnitsprisen pr. kvadratmeter for et hus den 1. januar 2014 aflæses til 12.500 kr. Dette giver, at den samlede pris for hus på 150 m² er: (150 m²)·(12.500 kr./m²) = 1.875.000 kr.
3. Man skal beregne prisen pr. kvadratmeter for et hus, der er på 150 m² og koster 2.000.000 kr. Denne er: (2.000.000 kr.)/(150 m²) = 13.333 kr./m²
4. Kvadratmeterprisen toppede ved 14.500 kr./m² i 2008. Det procentvise fald fra 2008 til 2014 er: [(14.500 - 12.500)/14.500]·100 % = 13,8 %
5. Kvadratmeterprisen er 8500 kr./m² i 2004 og stiger til 12.500 kr./m² i 2014. Man antager, at der sker et årligt procentuelt stigning på 4 % over de 10 år.
   Man bruger fremskrivnings-formlen og får: 8500·1,04¹⁰ = 12.500, hvilket passer med det som skulle vises.

Svar på opgave 2: Liggetider

1. På tegningen nendenunder deler en rød stiplet linje de liggetider, der er under henholdsvis over 120 dage. Linjen viser, at 33,5 % + 22,8 % = 56,3 % af lejlighederne har en liggetid på 120 dage eller derunder.
   
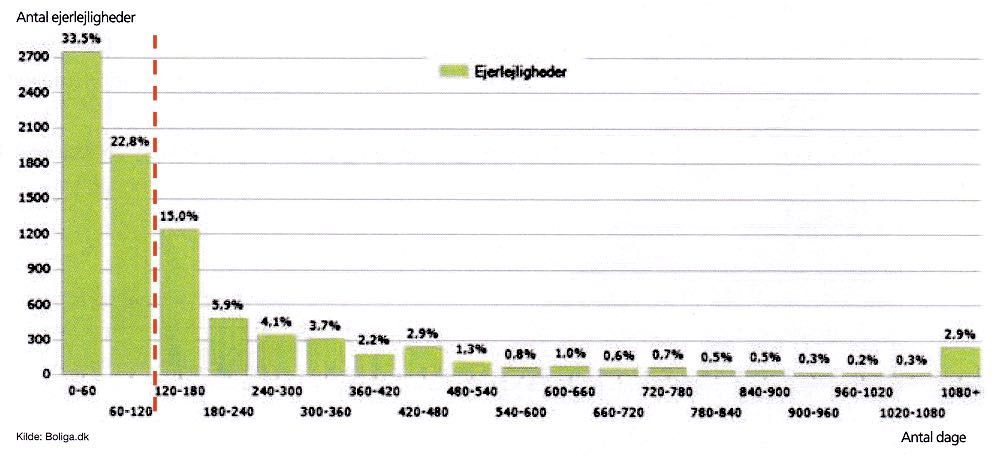
2. Helles påstand passer, idet mere end 50 % af liggetiderne i følge diagrammet har en liggetid på eller under 120 dage, og derfor må medianen, der svarer til de mindste 50 % af liggetiderne, også ligge på eller under 120 dage.
3. Helles påstand passer ikke, idet gennemsnittet trækkes op af de lange liggetider til højre i diagrammet.

Svar på opgave 3: Flyttepriser

1. 10.000 kr. + 6·(1249 kr.) = 17.494 kr.
2. Forskriften er 1249·x + 10.000, hvor x er antal timer og resultatet er prisen i kr.
3. Man skal finde x i ovenstående forskrift, når det samlede beløb er 16.895 kr. Man får: 1249·x + 10.000 = 16.895 ⇔ x = (16.895 - 10.000)/1249 = 5,520. Det vil sige, at det må højst tage 5 timer, hvis tilbud 1 skal være billigst
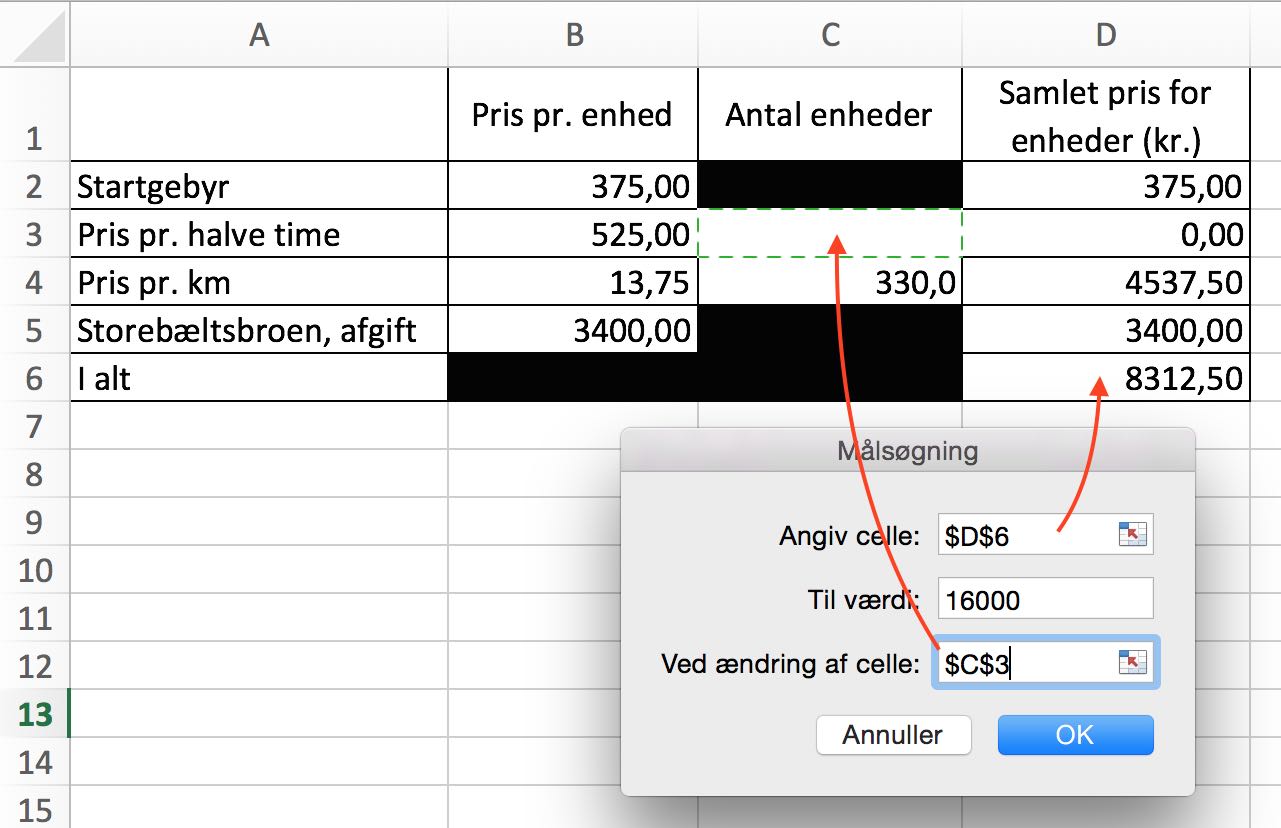
4. Man opstiller skemaet i Excel. Man finder værdien af feltet C3 ved hjælp af Funktioner - Målsøgning som vist. Man får resulatet, at flytningen må højst tage 14,6 timer, hvis prisen skal være 16.000 kr. eller derunder.
   

Svar på opgave 4: Højdemålinger i det gamle hus

1. Fra 1.3 1998 til 1.1 1999 er der 10 måneder. Fra 1.1 1999 til 1.9 1999 er der 8 måneder. I alt: 18 måneder, der er lig med 1 år og 6 måneder
2. Hun er vokset (170 - 85) cm = 85 cm på (2014 - 1999) år = 15 år. I gennemsnit er hun vokset: (85 cm/15 år) = 5,7 cm/år
3. Nedenfor er tegnet en graf i Excel for Helles højde som funktion af hendes alder.
   
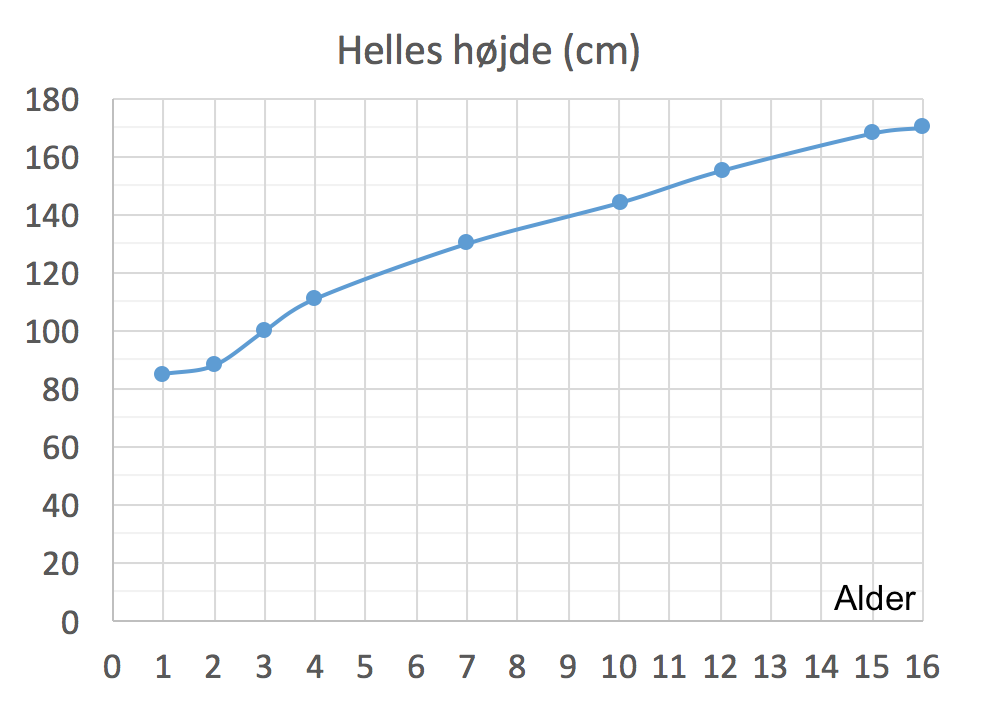
4. Hun voksede mest, da hun var mellem 2 og 3 år nemlig 12 cm.

Svar på opgave 5: Helles nye værelse

1. Arealet af gulvet er (5,5 m)·(4,3 m) = 5,5·4,3 m² = 23,7 m²
2. Højden måles til 3,9 cm på tegningen. Det svarer til, at værelset er 3,9 m højt.
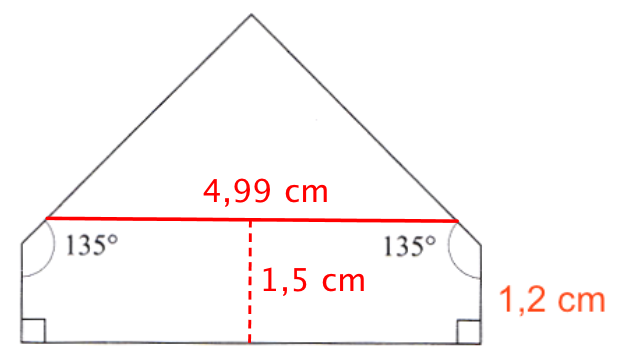
3. På tegningen nedenunder er det målt, at der er en længde i værelset på 4,99 cm, der har en loftshøjde på 1,5 cm eller mere. Rummets bredde måles til 4,3 cm på tegningen af værelset set fra oven. Det giver et boligareal på: (4,99 m)·(4,3 m) = 21,5 m²
   
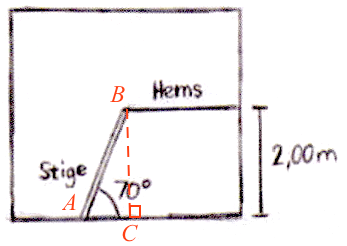
4. Nedenfor er der indtegnet en retvinklet trekant ABC på skitsen, hvor vinklen A er 70°, og dens modstående side er 2,0 m. Stigen er hypotenusen AB. Der gælder, at
   |AB|·sin(70°) = 2,0 ⇔
   |AB| = 2,0/sin(70°) ⇔
   |AB| = 2,128
   Det vil sige, at stigens længde er 2,13 m
   

Svar på opgave 6: Et ligebenet trapez

1. Nedenstående tegning er lavet i Geogebra.
   
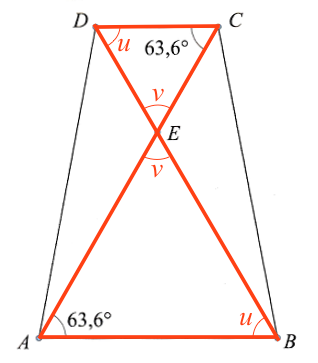
2. Begge trekanter indeholder vinklen 63,5°. De to vinkler kaldet v er ens, fordi de er topvinkler. De to vinkler kaldet u er ens som følge af reglen om, at summen af vinklerne i en trekant er 180°. Dermed er ΔABE og ΔCDE ensvinklede.
   
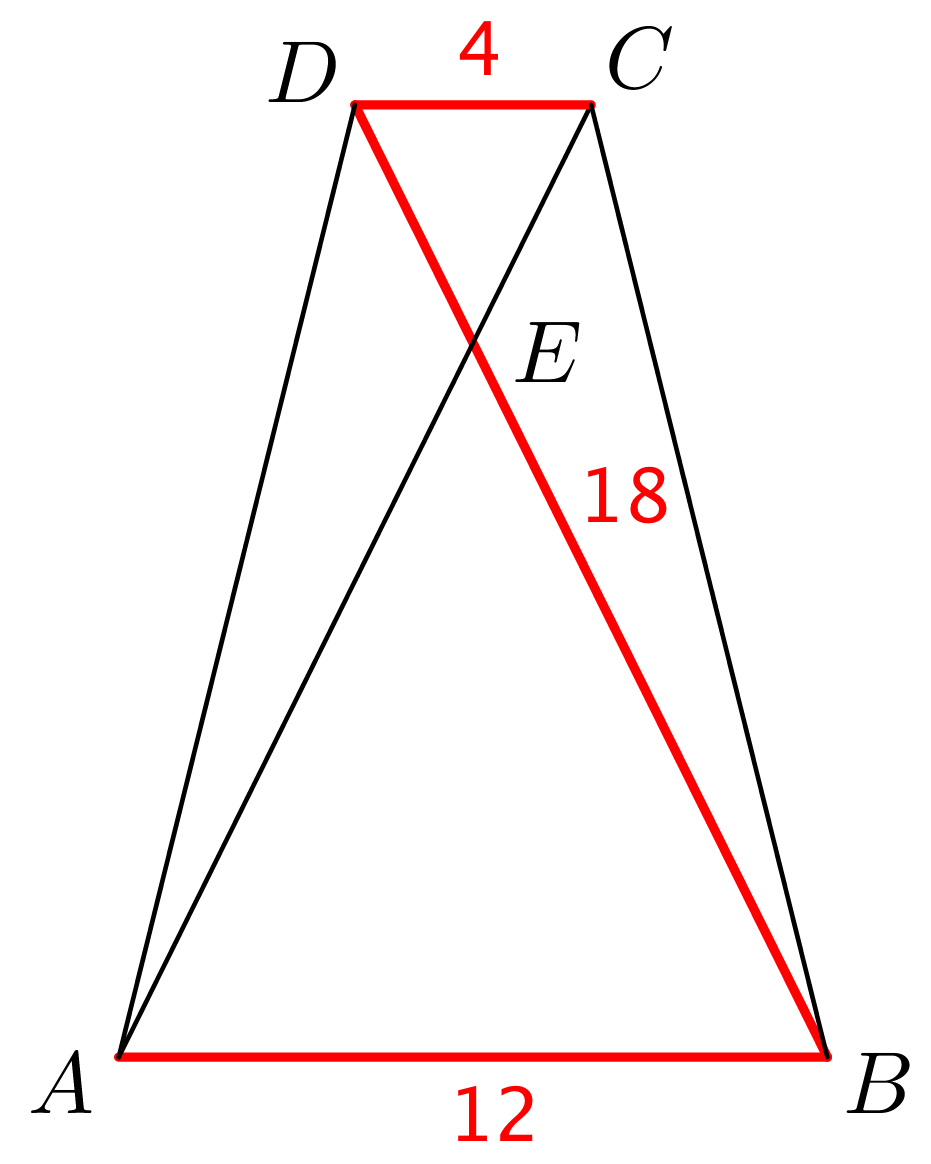
3. Man skal finde |DE| på nedenstående figur, hvor de kendte længder er sat ind. ΔABE og ΔCDE har skaleringsfaktoren: |AB|/|CD| = 12/4 = 3. Man ved, at |DE| + |BE| = 18. Desuden ved man, at |BE| = 3·|DE|. Man får: |DE| + 3·|DE| = 18 ⇔ |DE| = 18/4 = 4,5
   
4. Formlen for arealet af en vilkårlig trapez er h·(a+b)/2, hvor a og b er de parallelle sider og h er højden. Det giver her: Areal af trapez = tan(v)·[(a - b)/2]·(a + b)/2 = tan(72°)·(25 - 18)·(25 + 18)/4 = tan(72°)·7·43/4 = 231,6
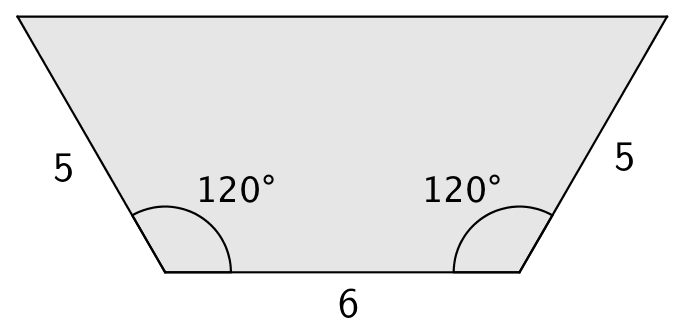
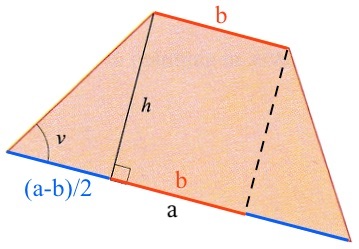
5. En ligebenet trapez kan inddeles i et rektangel og to ens retvinklede trekanter. Dette er vist på nedenstående tegning, hvor a er den lange af de parallelle sider og b er den korte. Vinklen v har den modstående katete h og den hosliggende katete (a - b)/2. Dermed gælder, at tan(v) = h/[(a-b)/2] ⇔ h = tan(v)·(a-b)/2.
   

Svar på opgave 7: Kvadrater i en additionstabel

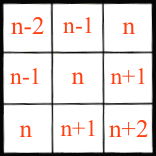
1. Summen af tal i første kvadrat er 4 + 5 + 6 + 5 + 6 + 7 + 6 + 7 + 8 = 54. Denne sum er 9 gange større end det midterste tal, som er 6 (9·6 = 54).
   Summen af tal i andet kvadrat er 11 + 12 + 13 + 12 + 13 + 14 + 13 + 14 + 15 = 117. Denne sum er 9 gange større end det midterste tal, som er 13 (9·13 = 117).
2. Når man går et felt mod venstre eller op i kvadratet bliver værdien af feltet een mindre, mens den bliver een større, når man går mod højre eller ned. Dette giver nedenfor viste værdier i kvadratet. Summen er: (n-2) + (n-1) + n + (n-1) + n + (n+1) + n + (n+1) + (n+2) = n + n + n + n + n + n + n + n + n - 2 - 1 - 1 + 1 + 1 + 2 = 9·n