Svar på opgave 1: På rejse til VM i fodbold

1. De skal vente fra 15:30 til 18:40, det er 3 timer og 10 minutter
2. Der er afgang fra København den 24. juni 14:35 dansk tid og ankomst i Sao Paulo den 25. juni 07:25 brasiliensk tid, som svarer til 07:25 + 5:00 = 12:25 dansk tid.
   Forskellen er (25 - 24) døgn + (12t + 25m) - (14t + 35m) = 1 døgn - 2t - 10m = 21 timer og 50 minutter
3. Biletterne koster: (2·495 + 2·175) USD = (990 + 350) USD = 1340 USD
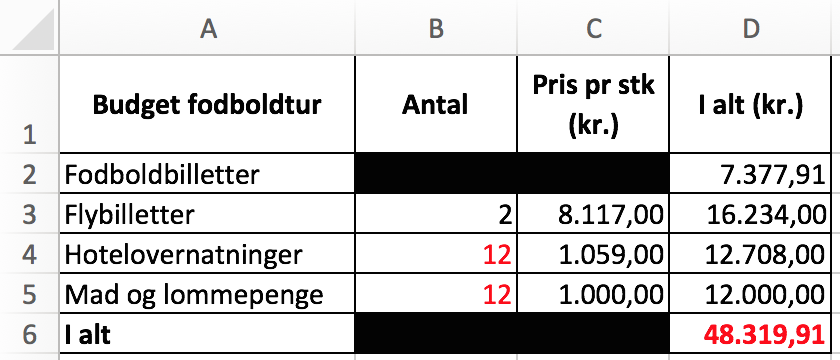
4. 1340 USD koster 7377,91 kr. Det vil sige, at 100 USD koster: 100·(7377,91/1340) kr. = 550,6 kr. Kursen for USD er dermed ca. 551
5. Løsningen er fundet i Excel ved at ændre antal dage indtil, man når et totalbeløb, der er større end 50,000 kr. Nedenfor ser man, at beløbet for 12 dage er mindre end 50.000 kr. For 13 dage er det større. De har dermed råd til at opholde sig i Brasilien i 12 dage
   

Svar på opgave 2: VM-fodbolden Brazuca

1. Boldens omkreds = diameter·π. Det vil sige, at boldens diameter = omkreds/π = (69,5 cm)/π = 22 cm
2. Rumfanget af en bold er (4/3)·π·r³, hvor r er boldens radius, som er lig med halvdelen af dens diameter. Det vil sige, at radius = (22 cm)/2 = 11 cm.
   Boldens rumfang er derfor: (4/3)·π·(11 cm)³ = 5.573 cm³ = 5.573 (0,1 dm)³ = 5,573 dm³ ≈ 5 L

Svar på opgave 3: Brasilien og Danmark

1. Brasiliens befolkning er: (201 mio mennesker)/(5,5 mio. mennesker) = 36,5 gange større end Danmarks
2. Befolkningstætheden i Brasilien er: (201 mio. mennesker)/(8,516 mio. km²) = 23,6 mennesker pr. km²
3. Københavns andel af Danmarks befolkningstal er: [(0,57 mio. mennesker)/(5,5 mio. mennesker)]·100 % = 10,4 %
4. Antallet af menensker i Brasilien, der bor i byer over 500.000, er: (201 mio. mennesker)·43 % = 86,4 mio. mennesker.
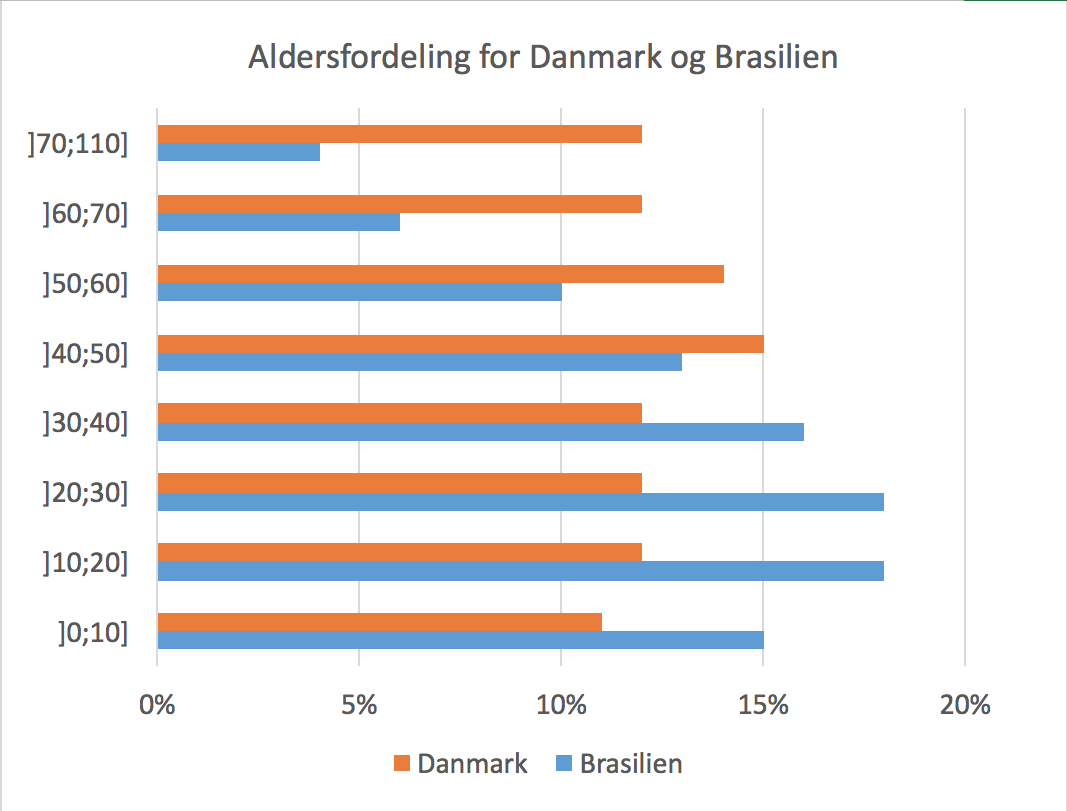
5. Aldersfordelingen i Danmark óg Brasilien vist i Excel. Der er omtrent lige mange mennesker i hver aldersgruppe i Danmark, mens der er flere unge end ældre i Brasilien.
   
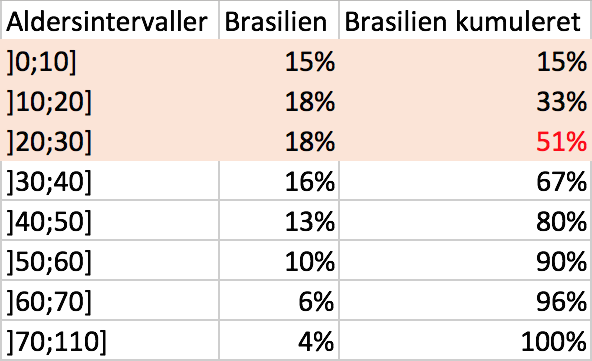
6. Medianen er den alder, som 50 % af befolningen ligger over. For at finde den, så lægger man procenterne sammen for hvert alderstrin fra mindst til størst og ser, hvornår man kommer over 50 %. Det giver nedenstående tabel. Heraf ses, at 51 % af Brasiliens er 30 år eller derunder. Det vil sige, at medianen for den Brasilianske befolknings alder er ca. 30 år
   
7. Man skal ud fra grafen finde det år, hvor Brasiliens befolkningstal var 2·75 mio. = 150 mio. mennesker. Dette årstal aflæses til 1990
8. Man bruger fremskrivningsformlen, hvor start-værdien er 75 mio., antal år er (2010 - 1961) = 49 og vækstraten er 2%.
   Dette giver en befokning i 2010 på (75 mio.)·(1+2%)⁴⁹ = 197,5 mio. ≈ 195 mio., der er det befolkningstal, som man kan aflæse på kurven. Det viul sige, at det passer, at der har være en årlig vækst på ca. 2%.
9. Danmarks befolkningstal voksede fra 4,5 mio. i 1961 til 5,5 i 2010. Hvis man forudsætter, at den vokser med 1 mio på 50 år så vil den være fordoblet efter 4,5·50 år = 225 år, det vil sige i år: 1961 + 225 = 2186

Svar på opgave 4: Kampplan

1. Antal lande i hver gruppe er 32/8 = 4
2. Antal kampe i en gruppe:
   Hold 1 mod de 3 andre hold. Det er 3 kampe.
   Hold 2 mod hold 3 og hold 4. Det er 2 kampe.
   Hold 3 mod hold 4. Det er 1 kamp.
   Samlet for alle grupper: 8·(1 + 2 + 3) kampe = 48 kampe i gruppespillet.
3. Bjarnes gevinst bliver (300 kr.)·4,33 = 1299 kr.
4. P(A) er sandsynligheden for at Brasilien vinder VM. Formlen for odds giver: 4,33 = 0,85/[P(A)] ⇒ P(A) = 0,85/4,33 ⇒ P(A) = 0,196
5. Bjarne har ikke ret fordi, at de satser 300 kr. og deres eneste chance for at få en netto gevinst er ved resultatet uafgjort.

Svar på opgave 5: Korde i en cirkel

1. Nedenstående tegning er lavet i Geogebra. Centervinklen er målt til 97,2°
   
2. Kordens længde bliver i følge formlen i den gule boks: k = 2·(4 cm)·sin(0,5·80°) = (8 cm)·sin(40°) = (8 cm)·0,6428 = 5,14 cm
3. Når centervinklen er 180° skal korden være lig med en diameter. Det vil sige, at korden i følge formlen skal være 8 cm. Man får: k = 2·(4 cm)·sin(0,5·180°) = (8 cm)·sin(90°) = (8 cm)·1 = 8 cm, hvilket viser, at formlen også passer for en centervinkel på 180°
4. Trekanten består af to sider, hvis længde er lig med radius og en side hvis længde er lig med korden. Hvis korden er lig med radius, har man en ligesidet trekant. I denne er alle vinkler lig med 60° og dermed er centervinklen = 60°
5. Ane har ret i sin påstand, fordi centervinklen er topvinkel i en ligebenet trekant og i denne gælder, at vinkelhalveringslinjen til topvinklen samtidig er median til grundlinjen, som her er lig med korden.
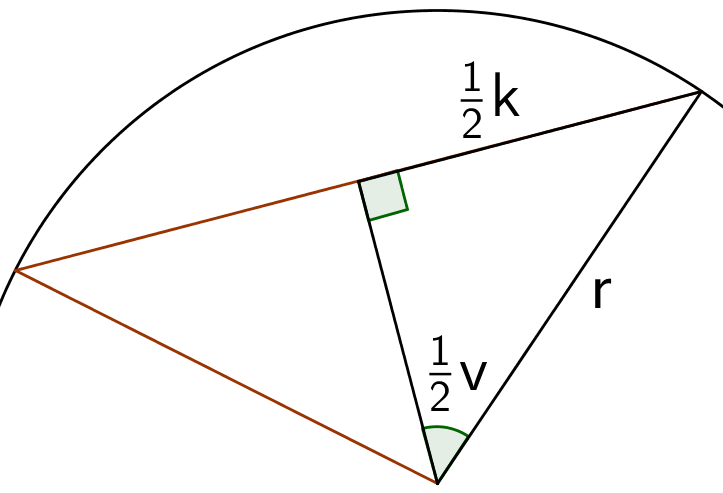
6. Som vist nedenfor kan trekanten kan deles op i to ens retvinklede trekanter. I hver af dem gælder: sin(v/2) = (modstående katete)/(hypotenuse) ⇒ sin(v/2) = (k/2)/r.
   
7. Man kan omskrive Anes formel til udtrykket i den gule boks på følgende måde:
   sin(v/2) = (k/2)/r ⇔
   r·sin(v/2) = k/2 ⇔
   k = 2·r·sin(v/2)