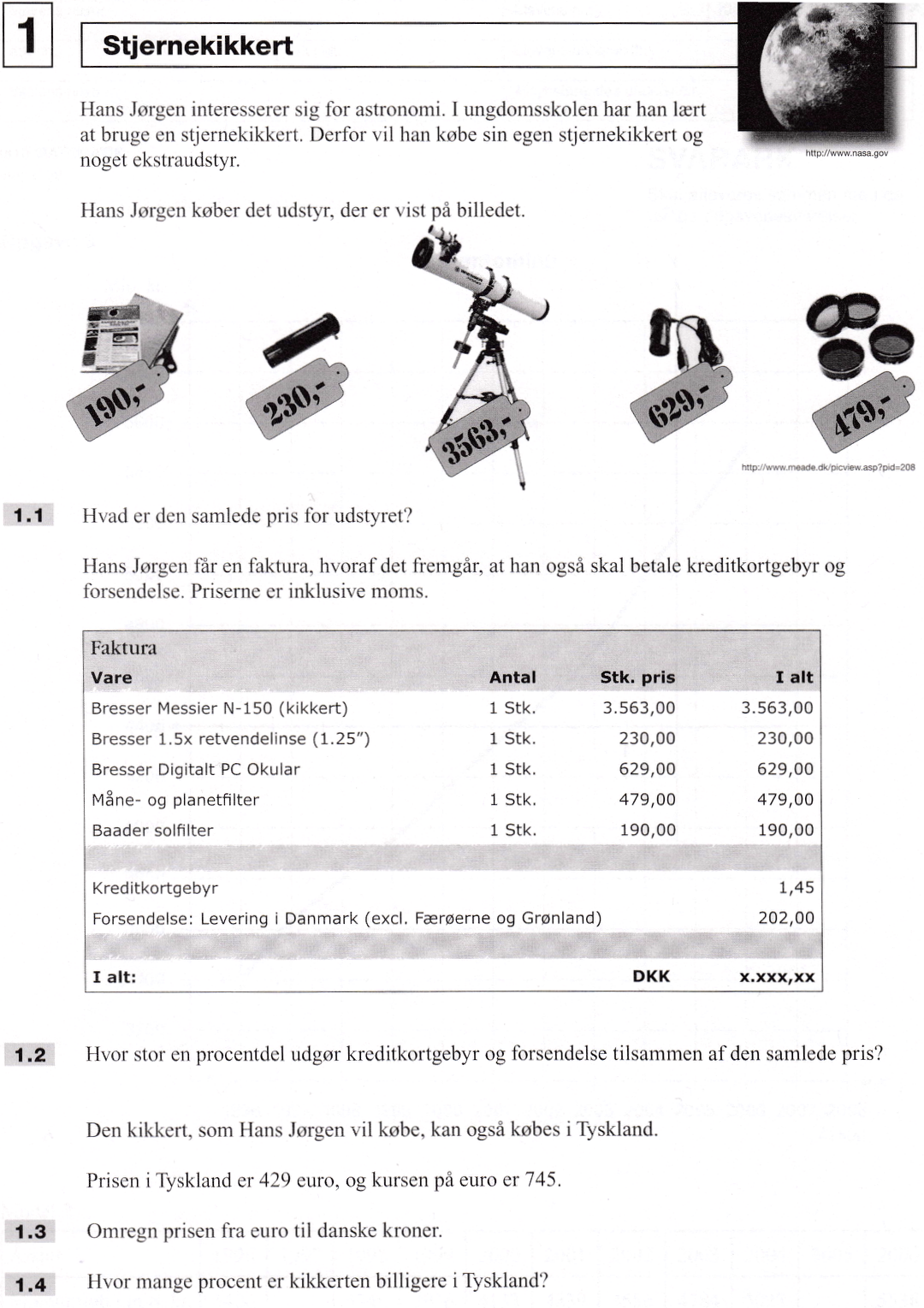
Svar på opgave 1: Stjernekikkert

1. Den samlede pris for udstyret er (190 + 230 + 3.563 + 629 + 479) kr. = 5.091 kr.

2. Kreditkort gebyr og forsendelse koster tilsammen: 1,45 kr. + 202 kr. = 203,45 kr. Den samlede pris med kreditkort gebyr og forsendelse er 5.091 kr. + 1,45 kr. + 202 kr. = 5.294,45 kr.

   Kreditkort gebyr og forsendelse udgør følgende procentdel af den samlede pris: [(203,45 kr.)/(5.294,45 kr.)]·100 % = 3,84 %

3. Kursen på euro betyder: prisen på 100 euro.

   Prisen på 100 euro er 745 kr., dvs. 100 euro = 745 kr. eller 1 euro = 7,45 kr.

   Prisen på kikkerten er 429 euro = 429·(1 euro) = 429·(7,45 kr.) = 429·7,45 kr. = 3.196,05 kr.

4. Antallet af kr. som kikkerten er billigere i Tyskland er: 3.563,00 kr. - 3.196,05 kr. = 366,95 kr.

   Dvs. den tyske pris er: (366,95/3.563,00)·100 % = 10,3 % billigere end den danske.

Svar på opgave 2: Jorden

1. En kugles omkreds er diameter gange pi, dvs. jordens omkreds er (12.740 km)·π = 40.024 km

2. En kugles overfladeareal er 4·π·r², hvor r = radius = diameter/2, som her = (12.740 km)/2 = 6.370 km.

   Dvs. jordens overfladeareal er 4·π·(6.370 km)² = 510 mio km²

3. Arealet der er dækket af saltvand er (510 mio. km²)·(71 %) = 362,1 km²

4. Den indre kerne ligger mellem 5200 km og 6300 km fra jordens overflade og udgør en kugle. Kuglens radius er (6370 - 5200) km = 1170 km

5. Den indre kernes rumfang er (4/3)·π·r³ =

   (4/3)·π·(1170 km)³ = 6,71 mia. km³

6. Forholdet mellem to kuglers rumfang kan beregnes som forholdet mellem deres radier opløftet i tredje potens, dvs.

   (jordens rumfang)/(kernens rumfang) = [(jordens radius)/(kernens radius)]³ =

   [(6370 km)/(1170 km)]³ = (6370/1170)³ = 161,4

   Dvs. jordens rumfang er 161 gange større end kernens.

7. Nedenfor er vist en tidslinje med universets opståen og nu.

   

8. Nedenfor er vist samme tidslinje som i ovenstående spørgsmål med de øvrige tidspunkter tilføjet.

   

Svar på opgave 3: Jupiter

1. Jupiters radius er dens diameter divideret med to = (142.984 km)/2 = 71.492 km

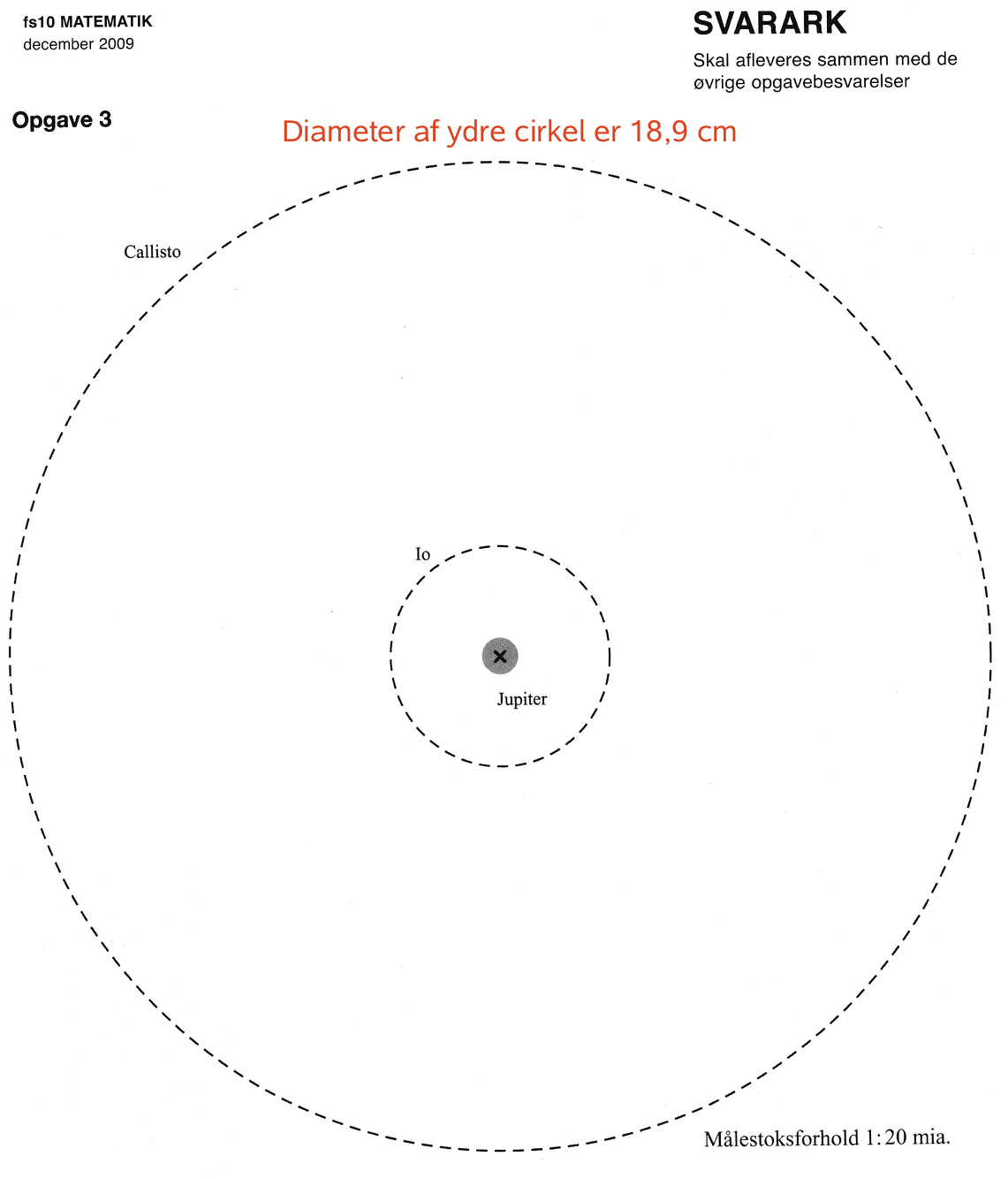
2. Diameteren i Callistos bane målt på papir er 18,9 cm. Dvs. radius af banen er 9,45 cm. Dette omregnes til km: 9,45·(1 cm) = 9,45·(0,01 m) = 0,0945·(1 m) = 0,0945·(0,001 km) = 0,0000945 km.

   Dette ganges med 20 mia. og man får, at Callistos bane-radius beregnet fra tegningen er (0,0000945 km)·20.000.000.000 = 1.890.000 km.

   Dette passer med Callistos rigtige bane-radius (afstand fra Jupiter) og dermed passer målestoksforholdet på 1:20 mia.

3. Man kan tegne banerne for de to sidste måner ved at beregne hvor mange gange større deres baner er end Io's. Dette er gjort i nedenstående tabel, hvor den tredje kolonne viser månernes bane-diameter divideret med Io's:

   

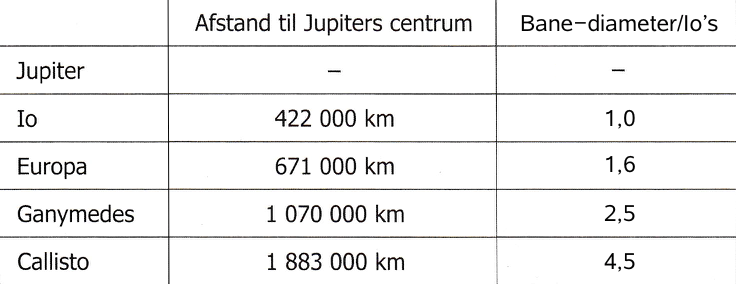
   På grundlag af tabellen tegnes de to midterste måners baner i Geogebra:

   

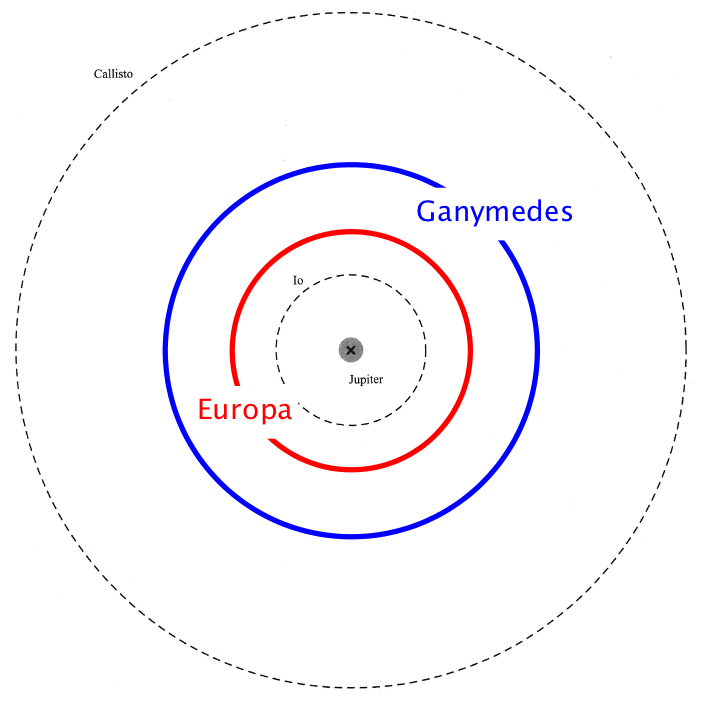
4. Europas omløbstid er: 1,55·10^-7·√[671.000³] timer = 85,195 timer = 85 timer

5. På 20 omløb bruger Io: 20·43 timer = 860 timer. Dette omregnes til døgn og timer:

   860 timer = 860·(1 time) = 860·(1/24 døgn) = 35,83 døgn = 35 døgn + 0,83 døgn =

   35 døgn + 0,83·(1 døgn) = 35 døgn + 0,83·(24 timer) = 35 døgn + 19,9 timer =

   35 døgn og 19,9 timer.

   Dvs. Europas omløbstid er 35 døgn og 20 timer

6. Lyset bevæger sig 90 mio. km på 5 min eller 90 mio. km pr. 5 min. Dette omregnes til km/s:

   Hastighed = (90 mio. km)/(5 min.) = (90.000.000 km)/(5·(60 s)) = (90.000.000 km)/(300 s) = 300.000 km/s

Svar på opgave 4: Orion

1. Lyset fra Rigel har været undervejs i 2009 - 1221 år = 788 år. Dvs. der er 788 lysår fra Rigel til jorden.

2. Man skal vide, hvor mange sekunder, der er på et år for at bruge samme enheder. 1 år = 365·(1 dag) = 365·(24 timer) = 365·24 (3600 sekunder) = 365·24·3600 s = 31.536.000 s.

   Et lysår er den distance lys bevæger sig på et år. Distance = hastighed gange tid, dvs. et lysår er:

   (300.000 km/s)·(31.536.000 s) = 9.460.800.000.000 km = 9,46·10¹² km

3. Afstanden til Betelguese er (427 lysår)·(9,46·10¹² km/lysår) = 4,04·10¹⁵ km

4. Lysstyrken for Rigel er 0,4⁰ = 1

   Lysstyrken for Bellatrix er 0,4² = 0,16

5. Nedenunder er grafen for y = 0,4^x tegnet i Geogebra.

   

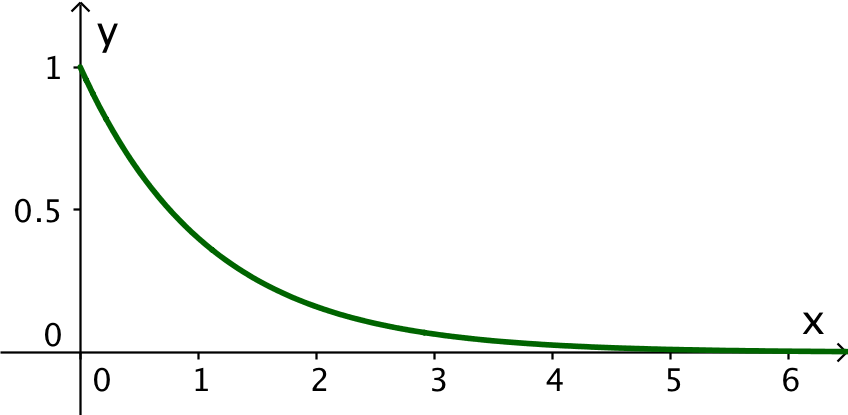
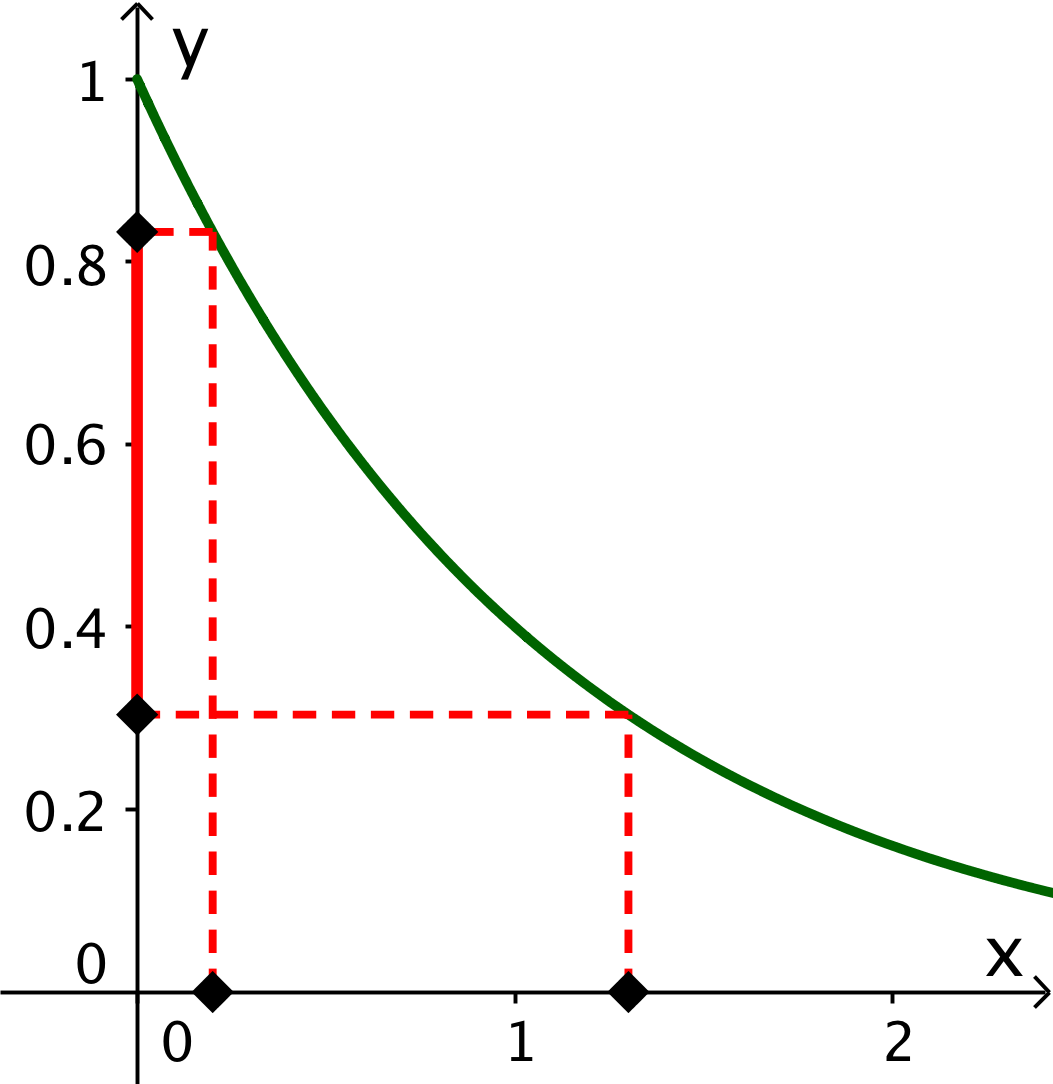
6. Nedenunder er størrelsesklasserne 0,2 og 1,3 afmærket på x-aksen. Ved hjælp af grafen findes de tilhørende y-værdier (lysstyrker) til 0,83 og 0,30. Disse lyssyrker er afmærket på y-aksen og intervallet mellem dem er tegnet op med et rødt linjestykke.

   

Svar på opgave 5: Galileo Galilei

1. Galilei blev (1642 - 1564) år = 78 år

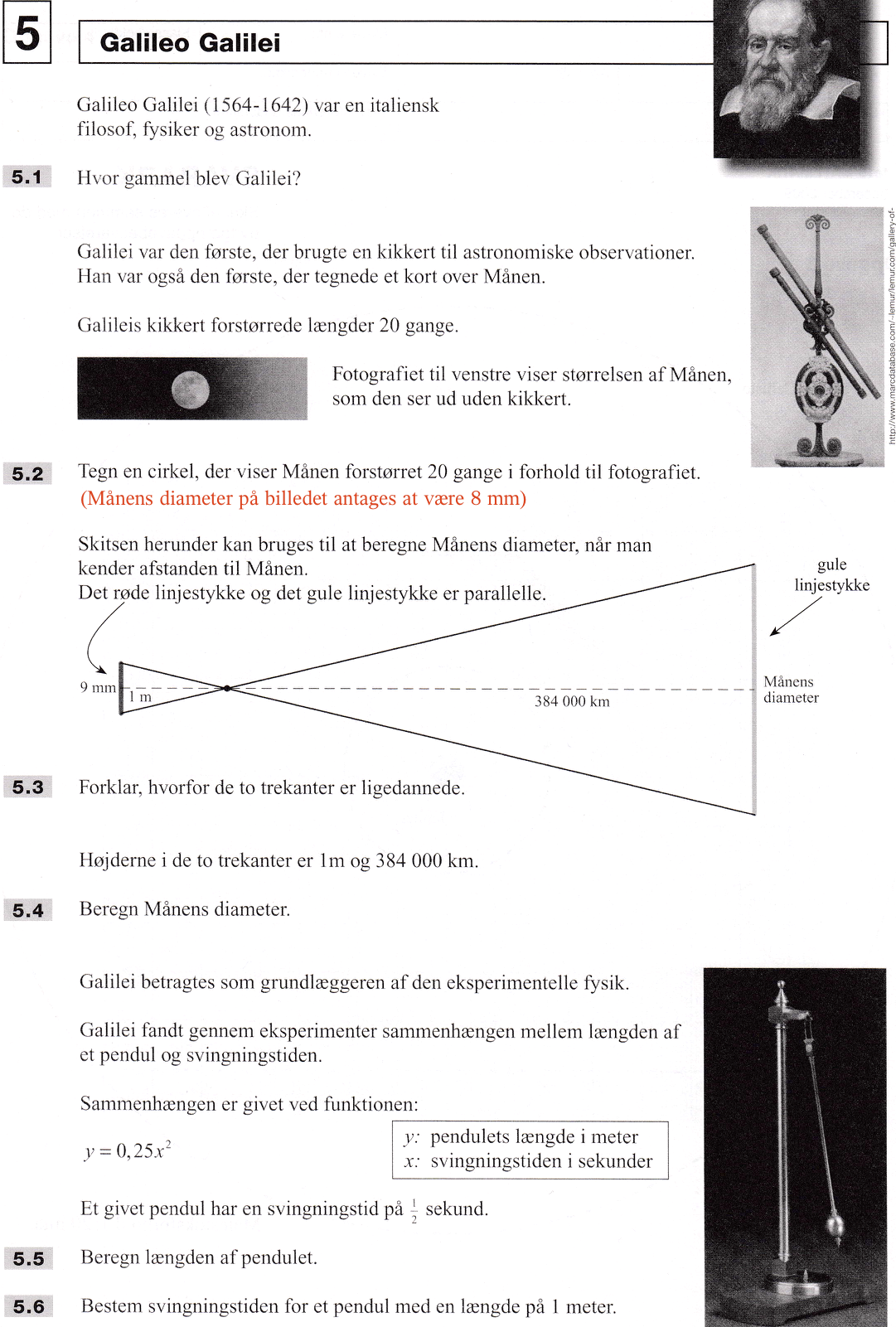
2. Man skal tegne en cirkel med en diameter, der er 20 gange månen på tegningen, som er 8 mm. Dette giver 20·8 mm = 160 mm. Dette er gjort nedenfor i Geogebra. Cirklen har en radius på 80 og dermed en diameter på 160.

   

3. De to trekanter er tegnet nedenunder. De to blå sider er parallelle. De to røde linjer er transversaler til de to parallelle linjer.

   

   De to transversaler krydser hinanden mellem de parallelle linjer. Dermed er de to trekanter, der dannes, ligedannede.

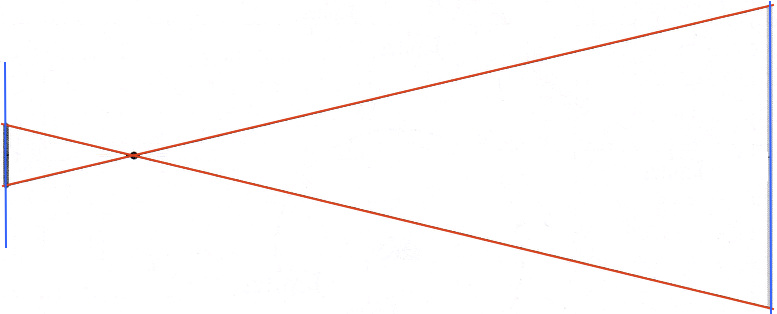
4. De to ligedannede trekanter er vist nedenunder. Den stiplede linje er højden i de to trekanter i forlængelse af hinanden.

   

   For to ligedannede trekanter vil forholdet mellem ensliggende sider og ensliggende højder være ens.

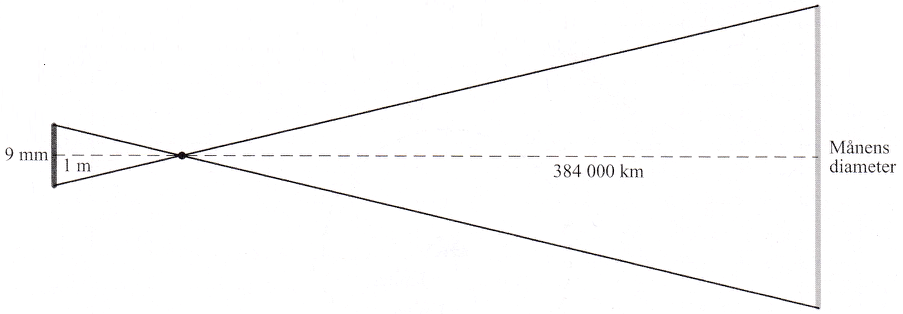
   Idet månens diameter kaldes x, får man: (384.000 km)/(1 m) = x/(9 mm) ⇔

   (9 mm)·(384.000 km)/(1 m) = x ⇔

   (9·(0,001·(0,001 km)))·(384.000 km)/(1·(0,001 km)) = x ⇔

   (9·0,000001 km)·(384.000 km)/(0,001 km) = x ⇔

   [(9·384.000·0,000001)/(0,001)] km = x ⇔

   (9·384.000·0,000001·1000) km = x ⇔

   (9·384) km = x ⇔

   x = 3.456 km

   Dvs. månens diameter er 3.456 km

5. Længden af pendulet er 0,25·(0,5)² m = 0,25·0,25 m = 0,0625 m = 0,063 m

6. For at finde svingningstiden skal man løse ligningen: 1 = 0,25·x² ⇔

   4·1 = 4·0,25·x² ⇔

   4 = x² ⇔

   x = √4 ⇔

   x = -2 eller x = 2. Her kun den positive løsning gyldig, da svingningstiden skal være et positivt tal.

   Dvs. svingningstiden er 2 s