Svar på opgave 1: Fra Felsted til Nordborg
- Han kører 11 km + 10 km hver vej = 2·(11 + 10) km om dagen = 42 km om dagen
- Transporttid på knallert = (21 km)/(30 km/t) = 0,7 timer = 0,7·(1 time) = 0,7·(60 min.) = 42 min.
-
På hverdage går den første færge fra Ballebro kl. 5:15. Derefter går de hver halve time. (Tabellens oplysninger om weekenden er overflødige).
Man skal regne ud hvilken færge, som han senest må tage. Man starter med at beregne, hvor lang tid han skal bruge på at køre fra færgen til Nordborg. Dette giver: (10 km)/(30 km/t) = (1/3)·(1 time) = (1/3)·(60 min.) = 20 min.
Dette trækkes fra kl. 7 og man får: 7:00 - 20 min. = 6:00 + 60 min - 20 min. = 6:40. Dvs. han kan ikke nå det, hvis han tager færgen 6:45 og må derfor tage den, der går 6:15.
Han skal derfor tage hjemmefra 22 min. før 6:15, hvilket giver: 6:15 - 22 min. = 5:00 + (60 min. + 15 min.) - 22 min. = 5:00 + 53 min. = 5:53 -
Knallert inkl. fører koster 25 kr. Han tager færgen to gange om dagen 200 dage om året. Det giver sammenlagt: 2·200·25 kr = 10.000 kr. om året.
Et værdikort kan bruges i stedet for billetter til en værdi af 1250 kr. Niels køber for 10000 kr. billetter. Det svarer til 10000/1250 værdikort = 8 værdikort. Prisen på 8 værdikort er 8·700 kr. = 5600 kr.
Dvs. værdikortene er 4400 kr. billigere om året.
Svar på opgave 2: Uddannelsen til klejnsmed
- Skoleopholdet er 10 + 10 + 10 + 5 uger = 35 uger
- Antal uger i praktik: antal uger i alt minus sum af skoleophold og grundforløb = 4·40 uger - (35 uger + 20 uger) = 160 uger - 55 uger = 105 uger
- Basisløn er antal timer gange sats (grundlæggende timeløn) = (160,33 timer)·(63,40 kr./time) = 10164,92 kr.
- Gennemsnitskarakteren er sum af karakterer divideret med antal karakterer = (10 + 2 + 7 + 7 + 4 + 12 + 7 + 4)/8 = 6,625
-
Skolekarakteren rundes op til 7. Man får gennemsnittet: (4 + 4 + 7 + 7 + 10 + 10 + 2 + 7)/8 = 6,325
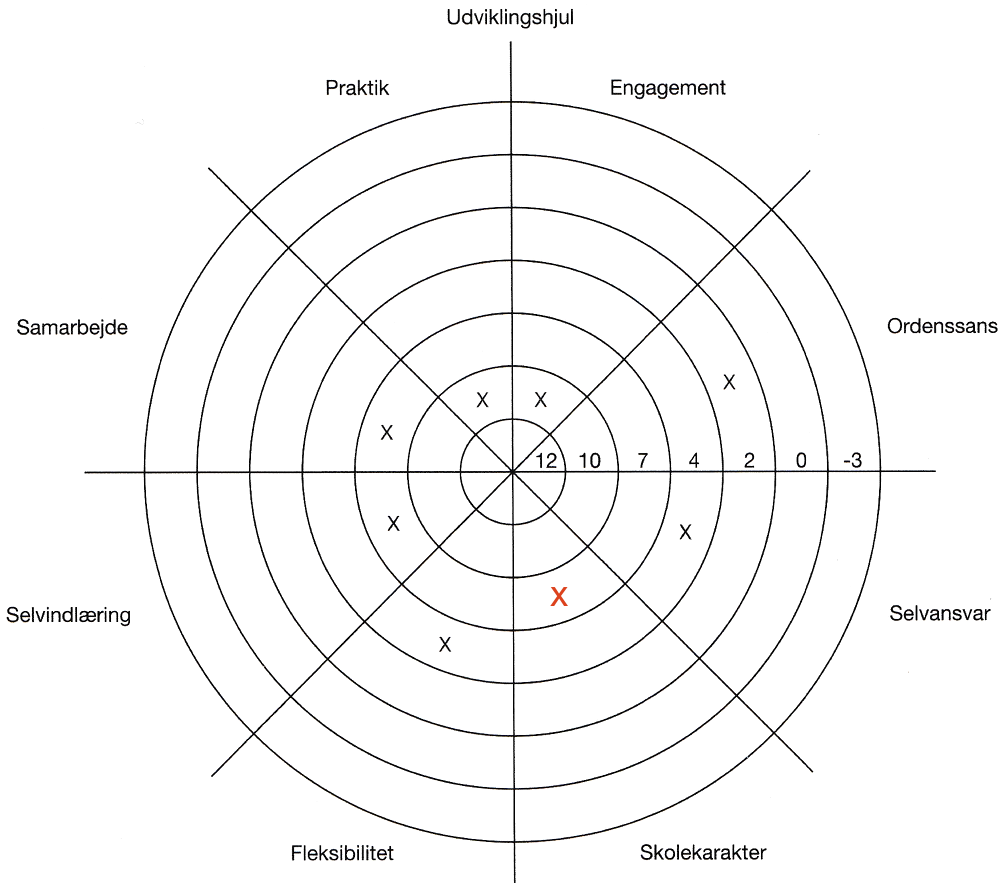
-
De 6,325 rundes op til 7. Dermed bliver den personlige lønsats 9,45 kr.

- Man skal gange 160,33 timer med den personlige sats på 9,45 kr./time. Dette sættes ind i skemaet som vist ovenfor.
-
A-skat = (10670,84 kr. - 3720 kr.)·39 % = (6950,84 kr.)·0,39 = 2710,83 kr.
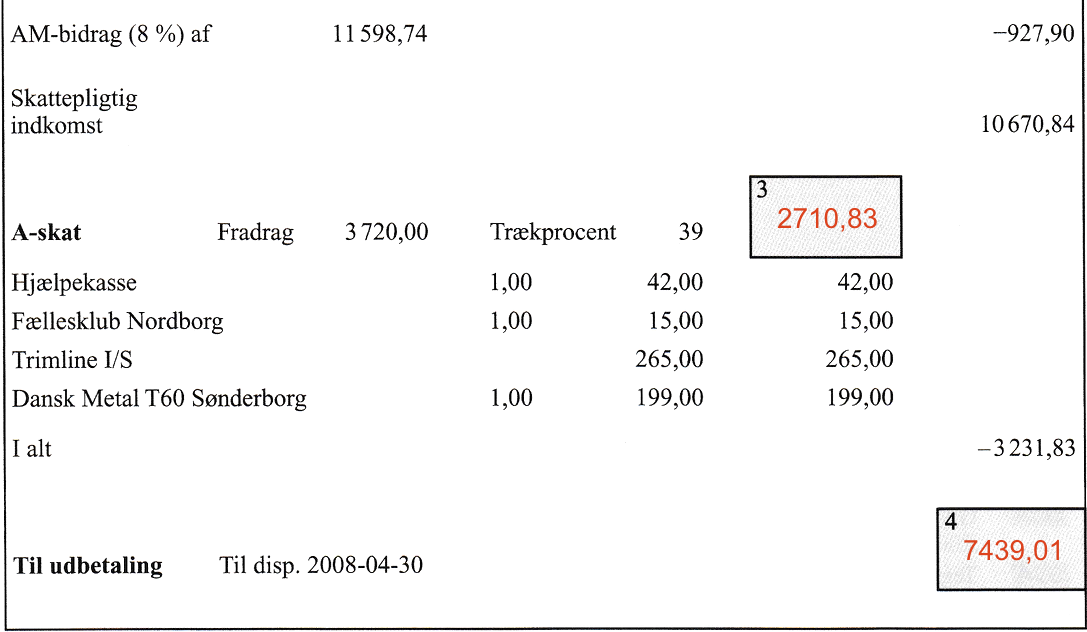
-
Man får i alt udbetalt skattepligtig indkomst minus skat = 10670,84 kr. - 3231,83 kr. = 7439,01 kr.
Dette sættes ind i skemaet som vist ovenfor.

Svar på opgave 3: Virksomhedens regnskab
- Bruttoresultat = (871 + 5366 - 5210) mio. kr. = 1027 mio. kr.
- Forholdet mellem produktionsomkostninger og nettoomsætning i 2005 er (4419/5339)·100 % = 82,8 %
- Forholdet mellem produktionsomkostninger og nettoomsætning i 2006 er (5270/(871 + 5366))·100 % = 83,5 %
- Bruttoresultat = [(871 + 5366) - (871 + 5366)·0,828] mio. kr. = (871 + 5366)·(1 - 0,828) mio. kr. = 6237·0,172 mio. kr. = 1072,8 mio. kr.
Svar på opgave 4: Virksomhedens medarbejdere
-
Man måler vinklen til 99,4° i Geogebra som vist nedenunder.
Det giver en andel af den samlede cikel på (99,4/360)·100 % = 27,6 %
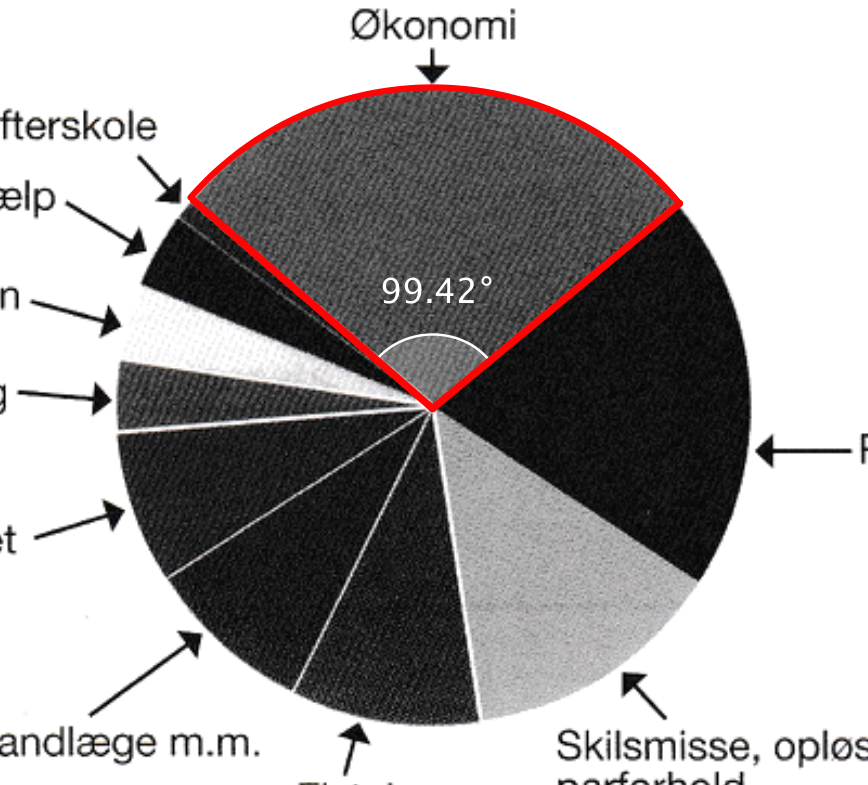
-
Det samlede beløb kaldes x. Man ved at 27,6 % af det samledede beløb er 1102 mio. kr., dvs. man får ligningen:
0,276·x = 1102 ⇒
x = 1102/0,276 = 3992,75 mio. kr.
Dvs. det samlede beløb som fonden uddelte i 2006 var 3992,8 mio. kr. - Den største procentvise stigning fandt sted fra 1950 til 1955. Her var stigningen: ((2321 - 581)/581)·100 % = 299 %
-
Udviklingen er vist nedenunder som en ret linje fra 1970 til 2015
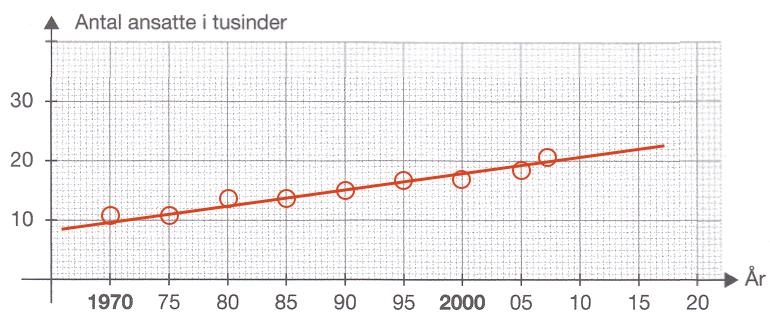
- Ud fra kurven aflæses antallet af ansatte i 2015 til ca. 22.000
Svar på opgave 5: Produkter
- Besvarelsen kræver en papirtegnig. Man skal vise at tegningen er dobbelt så stor som virkeligheden.
-
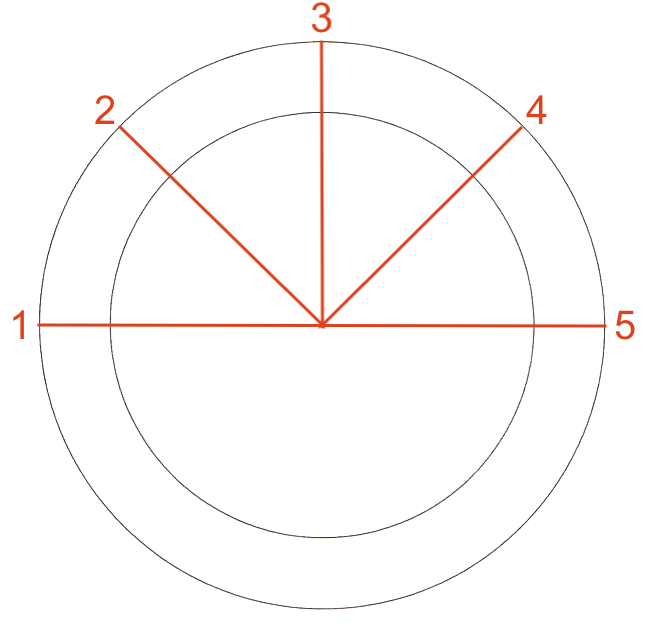
Konstruktionen af inddelingerne er vist nedenfor.
Man tegner en vandret linje gennem cirklens centrum og opretter den vinkelrette i centrum. Derved fremkommer to rette vinkler, som halveres. Tallene 1-5 skrives på med uret rundt hvor linjerne skærer cirklen.
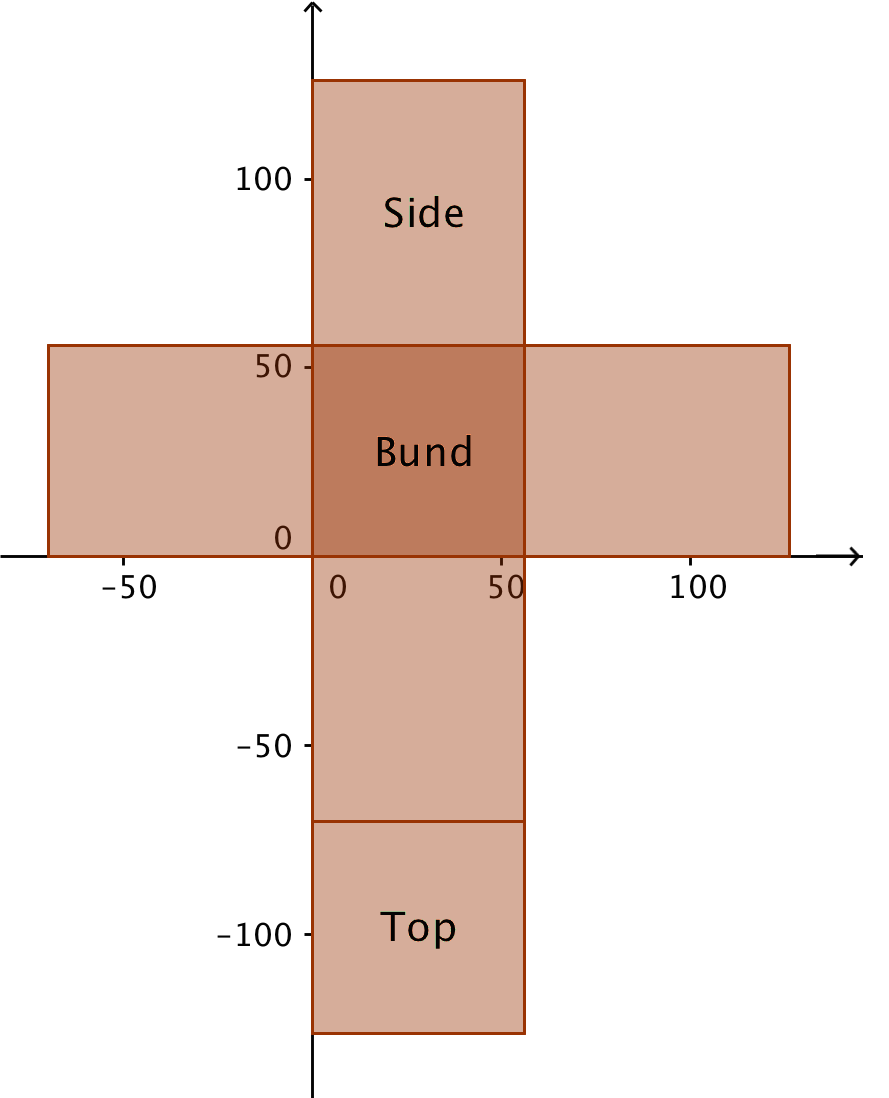
- Kassen grundflade skal minimum være 56 mm gange 56 mm. Højden skal minimum være 40 mm + 30 mm = 70 mm. Dvs. kassens dimensioner er LxBxH = 56 mm x 56 mm x 70 mm
-
Nedenunder er en udfoldning vist i Geogebra. Det rigtige målestoksforhold kan kun gengives på en papirtegning.