Svar på opgave 1: Sofie spiller ishockey

1. Den samlede pris for Sofies ishockey-udstyr er: (299 + 449 + 249 + 289) kr. = 1286 kr.

2. Med rabat skal Sofie betale følgende for udstyret: 1286 kr. - (1286 kr.)·12,5 % =

   (1.286 kr.)·(1 - 12,5 %) = (1.286 kr.)·(1 - 0,125) = (1.286 kr.)·0,875 = 1125,25 kr.

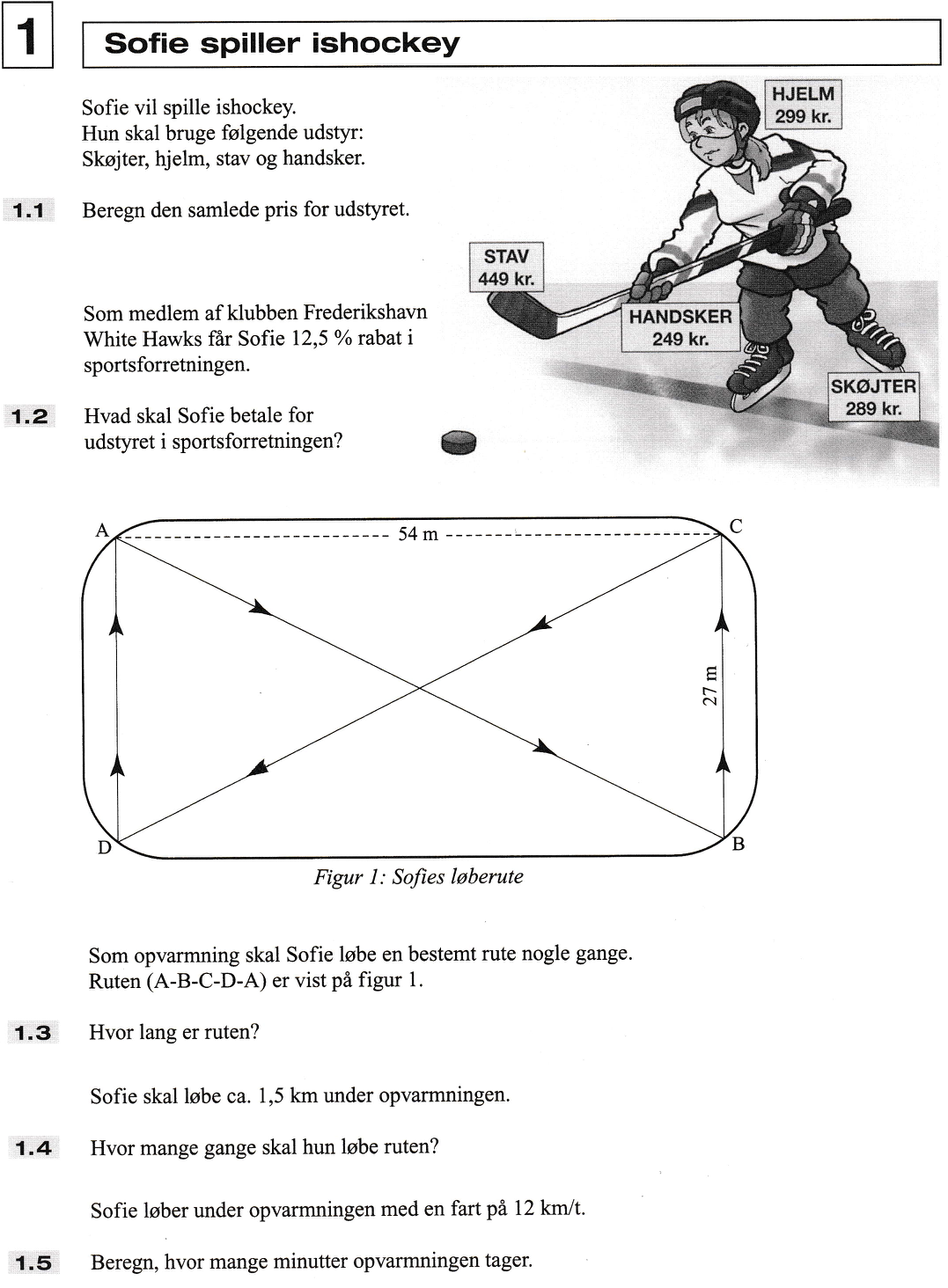
3. Punkterne ABC danner en retvinklet trekant, hvor |AB| er hypotenusen og kan findes ved hjælp af Pythagoras læresætning.

   

   Der gælder uden enheder at: |AB|² = 54² + 27² ⇔

   |AB|² = 3645 ⇒

   |AB| = √3645 ⇔

   |AB| = 60,4.

   Dvs. længden af ruten, som hun skal løbe, er 2·(27 m) + 2·(60,4 m) = 174,8 m

4. Hun skal løbe ruten (1500 m)/(174,8 m) = 8,58 gange = 9 gange

5. Tid = distance/fart. Dvs. den tid hun skal varme op i er (1500 m)/(12 km/t) = (1500 m)/[12·(1000 m)/(60 min.)] =

   [(1500·60)/(12·1000)] min. = 7,5 min.

Svar på opgave 2: Banen

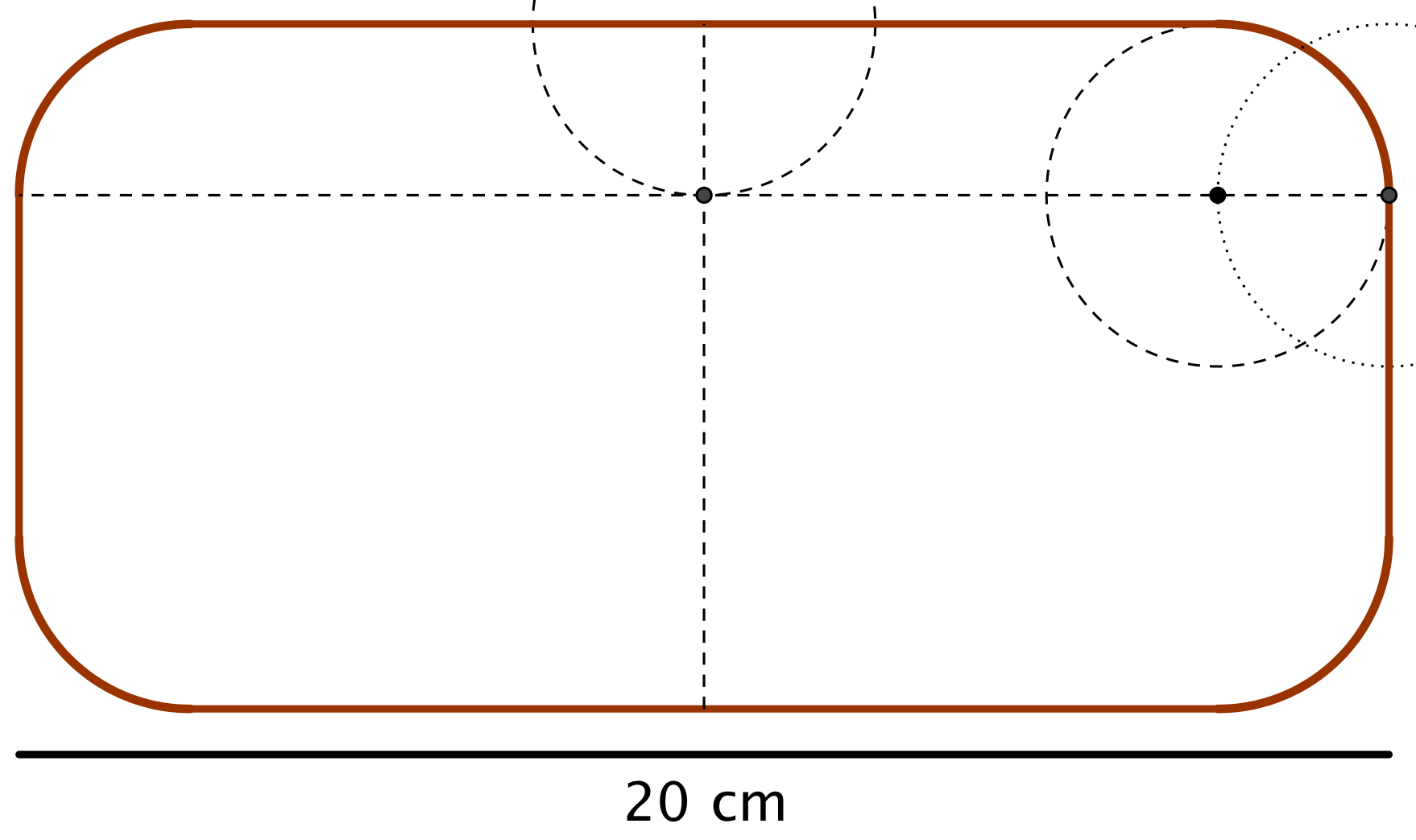
1. Nedenfor er tegningen af banen vist og banens længde på papiret.

   

2. Banen kan som vist nedenunder deles ind i fire firskellige figurer der kaldes A, B, C og D.

   

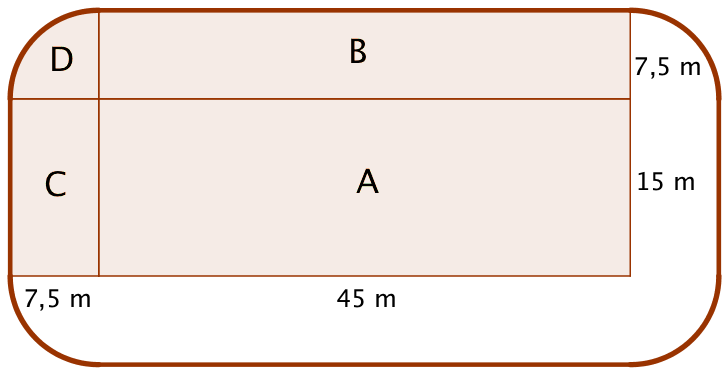
   Arealet af A er (15 m)·(45 m) = 675 m²

   Arealet af B er (7,5 m)·(45 m) = 337,5 m² (går igen to gange)

   Arealet af C er (7,5 m)·(15 m) = 112,5 m² (går igen to gange)

   De fire kvartcirkler mage til D har tilsammen arealet: π·(7,5 m)² = 176,715 m²

   Banens areal er: 675 m² + 2·337,5 m² + 2·112,5 m² + 176,715 m² = 1751,72 m² ≈ 1750 m²

3. Rumfanget af slangen er længde gange tværsnitsareal. Tværsnitsarealet er π·(radius)². Radius = (16 mm)/2 = 8 mm

   Man får følgende rumfang af køleslangen: (20 km)·π·(8 mm)² =

   (20·(1000 m))·π·(8·(0,001 m))² =

   (20.000 m)·π·(0,008 m)² =

   20.000·π·0,008² m³ =

   20.000·π·0,000064 m³ =

   4,02124 m³ = 4 m³

4. Isens rumfang er: rumgang af is med køleslange minus rumfang af køleslange. Rumfang af is med køleslange = areal af ishockeybane gange isens tykkelse.

   Man får følgende rumfang af is: (1750 m²)·(4 cm) - 4 m³ =

   (1750 m²)·(4·(0,01 m)) - 4 m³ =

   1750·0,04 m³ - 4 m³ =

   70 m³ - 4 m³ =

   66 m³

5. Massefylde er masse divideret med rumfang. Man får massefylden af is til:

   (49,44 tons)/(66 m³) =

   0,75 tons/m³

   (At det er mindre end 0,90 tons/m³, der er tabelværdien for is massefylde, kan forklares ved, at tabelværdien gælder is af rent vand uden luftbobler, og i praksis vil is altid indeholde luftbobler.)

Svar på opgave 3: Spillere

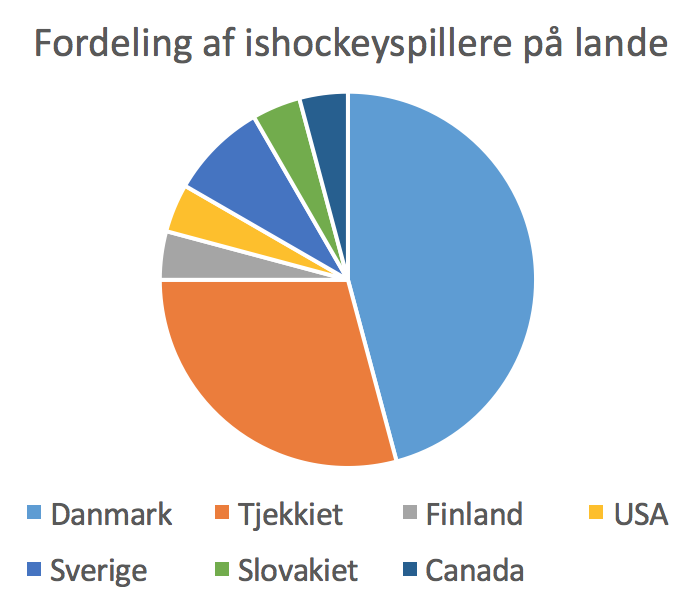
1. Nedenunder er et cirkeldiagram for fordelingen af Frederikshavns ishockeyspillere på lande lavet i Excel.

   

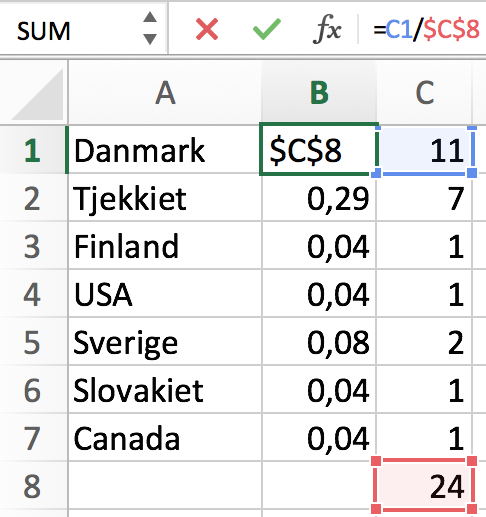
   Herunder er vist beregningerne af andele i Excel. Formlen =C1/$C$8 betyder, at summen på 24 spillerere, der står i feltet C8, holdes fast i nævneren hele vejen ned.

   

   Sådan markerer man de data, som skal bruges i diagrammet:

   

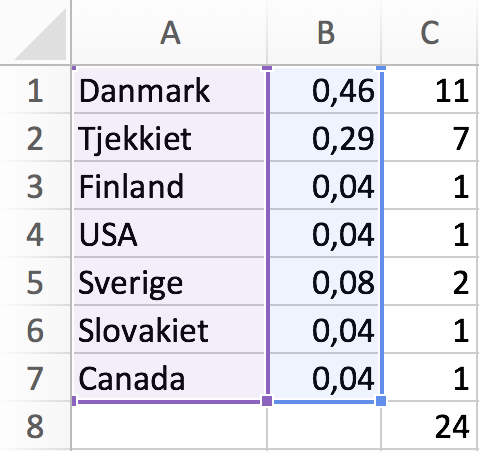
2. Der er 11 danske og 24 - 11 = 13 udenlandske spillere. Andelen af udenlandske spillere er (13/24)·100 % = 54,2 %.

   Dvs. Frederikshavn har lidt flere udenlandske spillere end gennemsnitet

3. Aldersgennemsnittet er [(24 + 16 + 22 + 27 + 26 + 21 + 21 + 31 + 21 + 21 + 19 + 29 + 41 + 31 + 21 + 24 + 32 + 24 + 31 + 36 + 29 + 24 + 26 + 29)/24] år = 26,1 år

4. Nedenunder er hyppighederne (antallet i hvert interval) indsat med rødt.

   

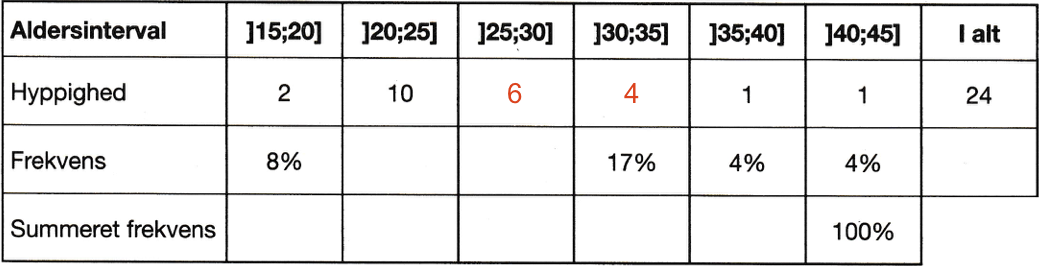
5. Frekvenserne er hyppighederne divideret med det samlede antal spillere, som er 24. De er indsat med rødt nedenunder. Frekvenser skal summere op til 100 %.

   

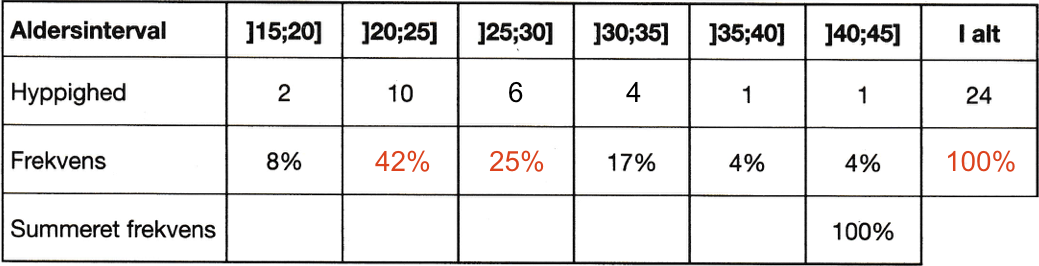
6. De summerede (eller kumulerede) frekvenser er vist i skemaet nedenunder.

   

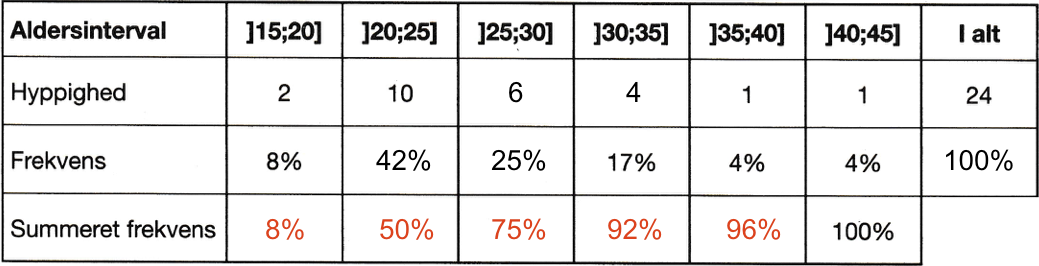
7. De summerede frekvenser er vist i en sumkurve nedenunder. Man sætter den mindste alder (15 år) i første interval til 0 %. Dernæst indsætter man de summerede frekvenser fra tabellen ud fra de øvre grænser i hvert interval.

   

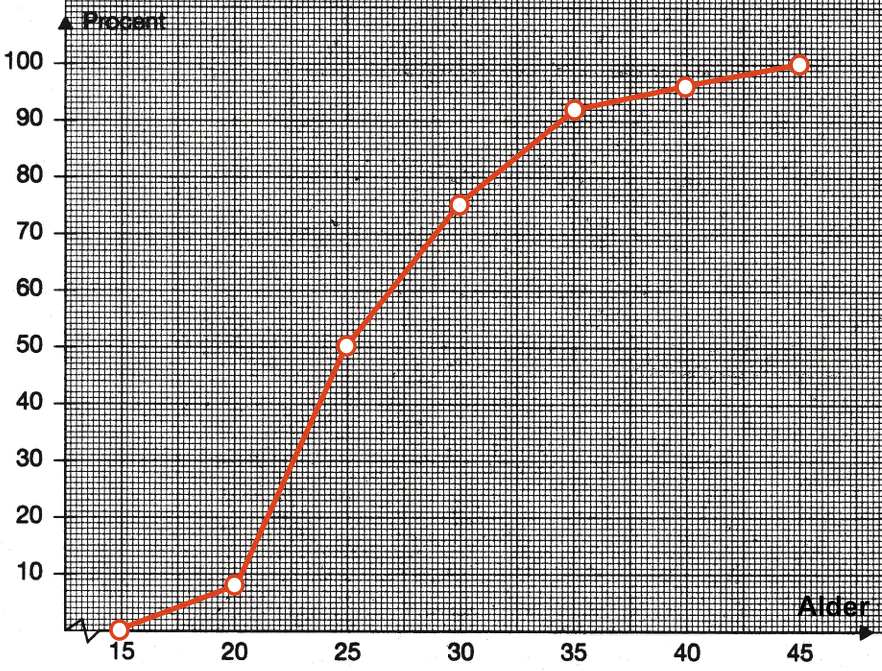
   Kurven viser, at ingen af spillerne er yngre end 15 år. 50 % er yngre end 25 år og 100% er yndre end 45 år.

8. Medianen aflæses af sumkurven som vist nedenunder med hvide pile. Man finder det tal på x-aksen (eller første-aksen), der svarer til 50% på y-aksen (eller anden-aksen).

   

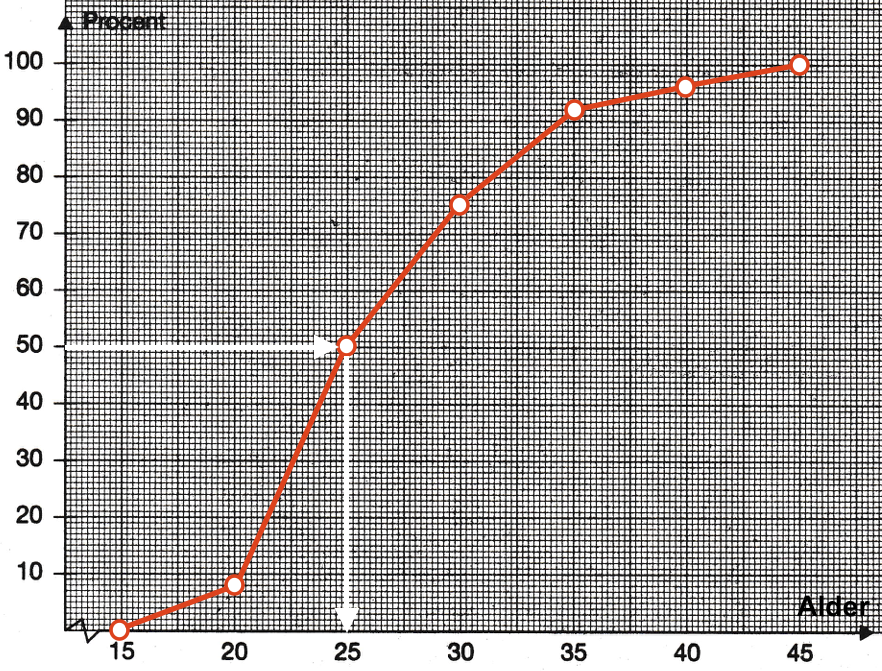
   Det ses, at medianen er 25 år

9. Medianen er den alder, som halvdelen af spillerne har eller ligger under

Svar på opgave 4: Resultater og stillinger

1. SønderjyskE skal spille 6 gange mod hver af de 2 andre hold i SønderjyskE's derbygruppe og derudover 4 gange mod hver af de 3 hold i hver af de 2 andre derbygrupper.

   Det giver tilsammen 6·2 + 4·3·2 = 36

2. Der er 9 hold, der skal spille 36 kampe hver. Hvis man regner på den måde er alle kampe talt to gange, idet den samme kamp både bliver talt som en kamp mellem hold A og hold B og som en kamp mellem hold B og hold A.

   Det giver tilsammen 9·36/2 kampe = 168 kampe.

3. Nedenunder tabellen er der vist med rødt de kampe for Frederikshavn White Hawks, der giver point.

   

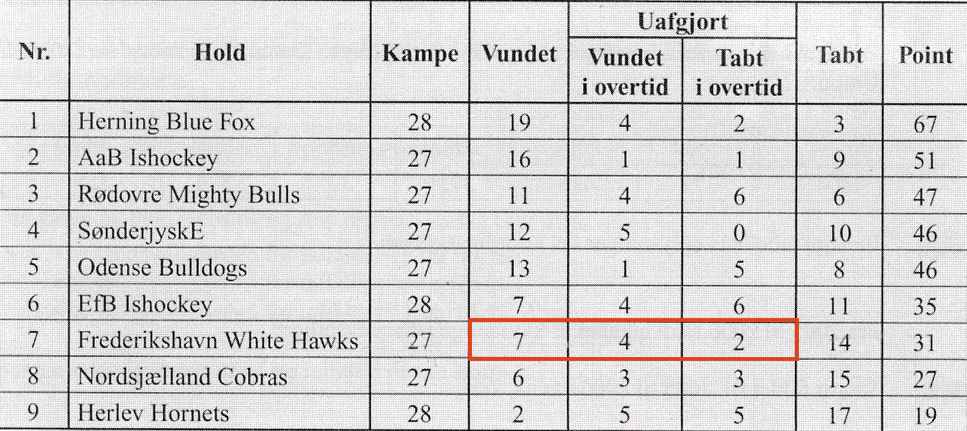
   Der er 7 vundne kampe, som giver 3 point hver, 4 uafgjorte kampe som giver 2 point, fordi Frederikshavn scorede i overtiden, og 2 kampe som endte uafgjort og kun giver 1 point, fordi det andet hold vandt i overtiden.

   Dette giver tilsammen følgende antal point: 7·3 + 4·2 + 2·1 = 31

4. På skemaet nedenunder er de hold, der kan komme på tredjepladsen efter næste runde indrammet med rødt.

   

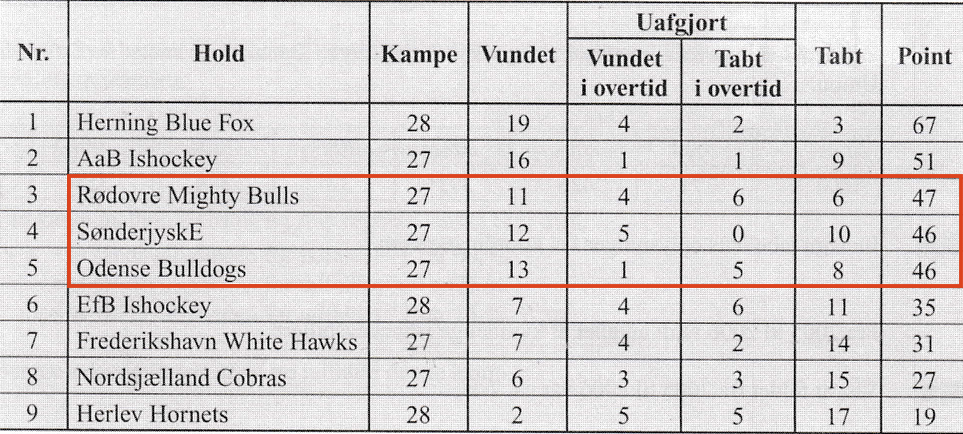
   Rødovre Mighty Bulls taber og har fortsat 47 point.

   SønderjyskE spiller uafgjort og vinder overtiden. Det giver 2 ekstra point, og de har samlet 48 point.

   Odense Bulldogs vinder og får 3 point. De har i alt 49 point.

   Dvs. Odense Bulldogs ligger på tredjepladsen efter den næste spillerunde.

Svar på opgave 5: Kvindelige ishockeyspillere

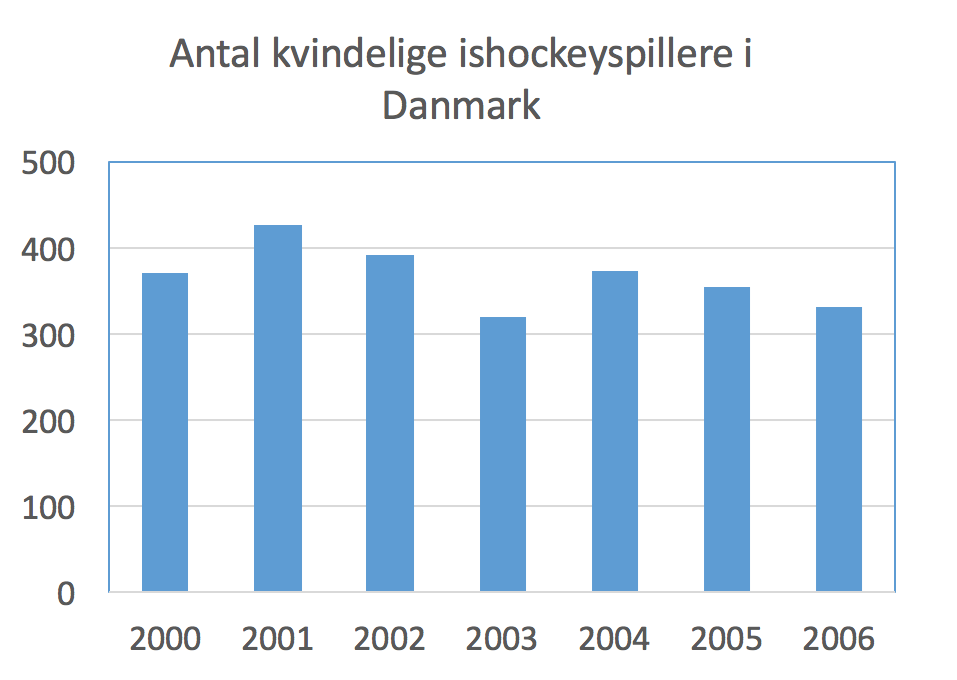
1. Herunder er vist et søjlediagram lavet i Excel over udviklingen i antallet af kvindelige ishockeyspillere i Danmark fra 200 til 2006.

   

2. Faldet var fra 355 i 2005 til 331 i 2006, dvs. start = 355 og slut = 331. Dermed er faldet i procent:

   [(355 - 331)/355]·100 % = 6,8 %

3. Man skal bruge fremskrivningsformlen eller opsparingsformlen: K = K₀·(1 + r)ⁿ, hvor K₀ = 331, r = -7% og n = 2009-2006 = 3. Man skal finde K. Man får:

   K = 331·(1 - 7%)³ = 331·(1 - 0,07)³ = 331·(0,93)³ = 266,24

   Dvs. antallet af kvindelige ishockeyspillere i 2009 vil være 266

4. Man skal løse ligningen 331/2 = 331·0,93^x, hvor x er antallet af år, der går før antallet af kvindelige ishockeyspillere er halveret. Det giver:

   331/2 = 331·0,93^x ⇔

   (331/2)/331 = 0,93^x ⇔

   1/2 = 0,93^x ⇔

   ln(1/2) = ln(0,93^x) ⇔

   ln(1/2) = x·ln(0,93) ⇔

   ln(1/2)/ln(0,93) = x ⇔

   x = 9,55

   Dvs. antallet af kvindelige ishockeyspillere vil være halveret efter 10 altså i 2016

   (Kontrol af afrunding. Man skal finde det første år, hvor antallet af spillere er mindre eller lig med 331/2 = 165,5.

   Efter 9 år er antallet: 331·0,93⁹ = 172,3, dvs. større end halvdelen.

   Efter 10 år er antallet: 331·0,93¹⁰ = 160,2, dvs. mindre end halvdelen.)

Svar på opgave 6: Ishockey og spil

1. Oddset for, at SønderjyskE vinder kampen, er 2,20, som det fremgår af skemaet:

   

2. Jørgen spiller 20 kr. på odds 4. Hvis dette resultat er det rigtige, vil det give en gevinst på (20kr.)·4 = 80 kr.

3. Odds for "1" er (87%)/(60%) = 87/60 = 1,45

   Odds for "x" er (87%)/(25%) = 87/25 = 3,48

   Odds for "2" er (87%)/(15%) = 87/15 = 5,80

4. Sandsynligheden (i %) for udfaldet "1" kaldes x. Man skal finde x af ligningen:

   (87%)/x = 2,9 ⇔

   (87%) = 2,9·x ⇔

   (87%)/2,9 = x ⇔

   x = 30 %

   Dvs. udfaldet for udfaldet "1" er 30 %

5. Det største samlede odds får man ved at gange de odds, der er markeret med rødt i skemaet nedenunder:

   

   Det største samlede odds i de to kampe er 4,00·6,35 = 25,4

6. Hvis man spiller på en kombination, skal begge resultater være rigtige for, at man får gevinst.

   Hvis man spiller på to enkelstående kampe, får man gevinst bare det ene resultat er rigtig.

   Antag at Jørgen spiller enten 2 kr. på kombination eller 1 kr. på hvert af de to resulater enkeltvis.

   Hvis ingen af resultaterne er rigtige, giver ingen af fremgamgsmåderne gevinst.

   Hvis "x" i kamp 1 er rigtigt, mens "x" i kamp 2 er forkert, vil kombinationen ikke give gevinst, mens spil på enkeltresulateter vil give 4 kr.

   Hvis "x" i kamp 1 er forkert, mens "x" i kamp 2 er rigtigt, vil kombinationen ikke give gevinst, mens spil på enkeltresulateter vil give 6,35 kr.

   Hvis begge resultaterne er rigtige giver kombinationsspil 25,40 kr. i gevinst, mens spil på enkeltkampe giver 4,00 kr. + 6,35 kr. = 10,35.

   Samlet set giver kombinationsspil 25,40 kr., mens spil på enkeltkampe giver 20,70 kr.

   Dvs. i dette tilfælde vil kombinationsspil kunne betale sig.