Svar på opgave 1: Operaøen

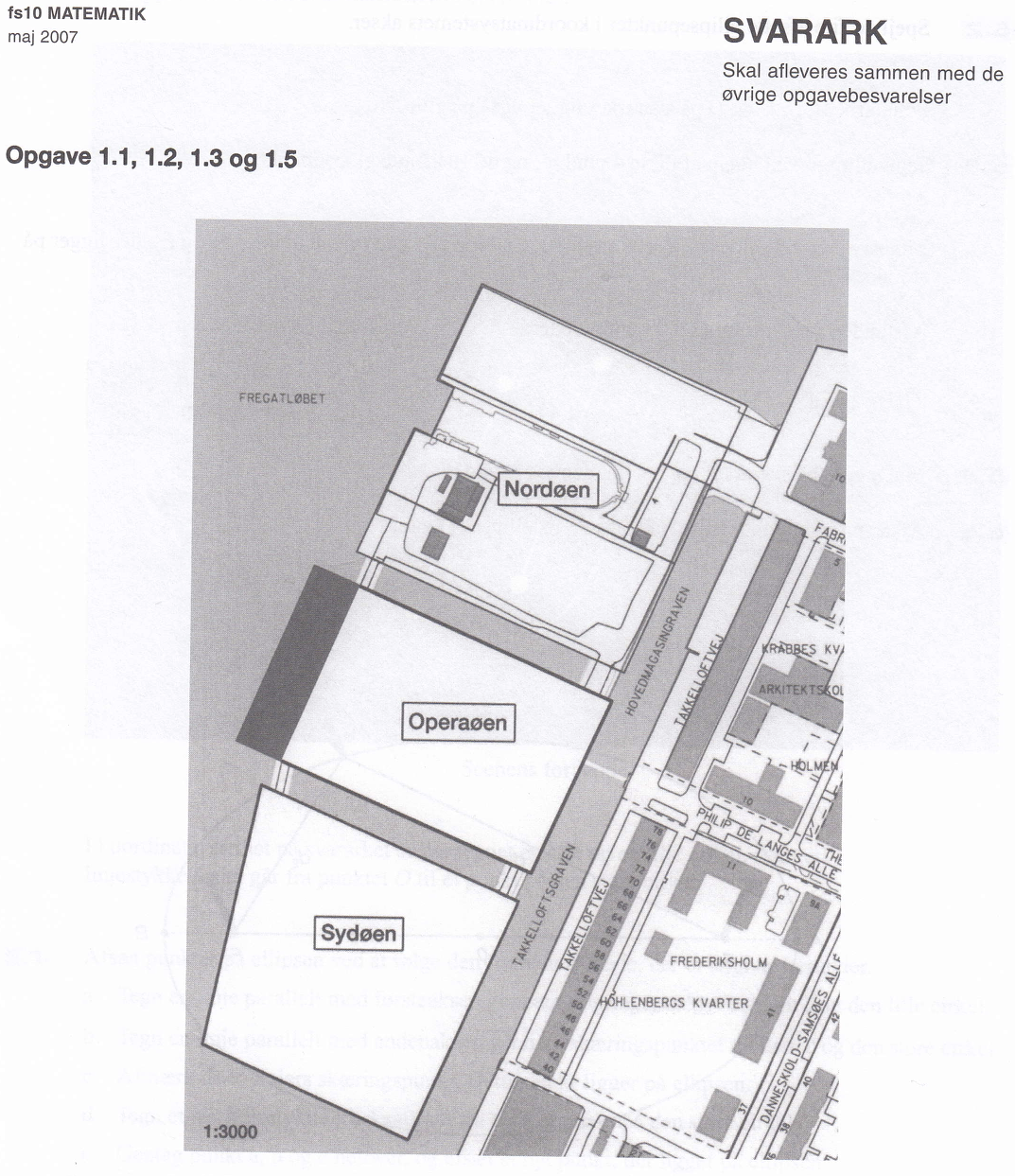
1. Operaøen er en rektangel og Sydøen er en trapez

2. Rektangel: modstående sider er lige store og parallelle, alle vinkler er rette.

   Trapez: to af siderne er parallelle.

3. Operaøens areal: (5,8 cm)·3000·(3,4 cm)·3000 = 177.480.000 cm² = 177.480.000·(0,01 m)² = 177.480.000·0,0001 m² = 17.748 m²

   Sydøens areal: (4,7 cm)·3000·[(5,0 cm)·3000 + (4,0 cm)·3000]/2 = (4,7 cm)·3000·(9,0 cm)·3000/2 = 190.350.000 cm² = 190.350.000 (0,01 m)² = 190.350.000·0,0001 m² = 19.035 m²

   Areal i alt: 17.748 m² + 19.035 m² = 36.783 m²

4. Det nuværende areal er 36783 m² + 22671 m² = 59454 m².

   Forøgelsen i areal er: 59454 m² - 54767 m² = 4687 m²

5. Rumfang er areal gange dybde. Areal = (0,9 cm)·3000·(3,4 cm)·3000 = 2754 m²

   Rumfang = 2754·7 m³ = 19278 m³

6. Jorden til opfyldningen vejer: (19278 m²)·(1500 kg/m³) = (19278 m²)·(1,5 tons/m³) = 28917 tons.

   Antal vognlæs = (28917 tons)/(30 tons/vognlæs) = 963,9 vognlæs = 964 vognlæs

Svar på opgave 2: Operaen

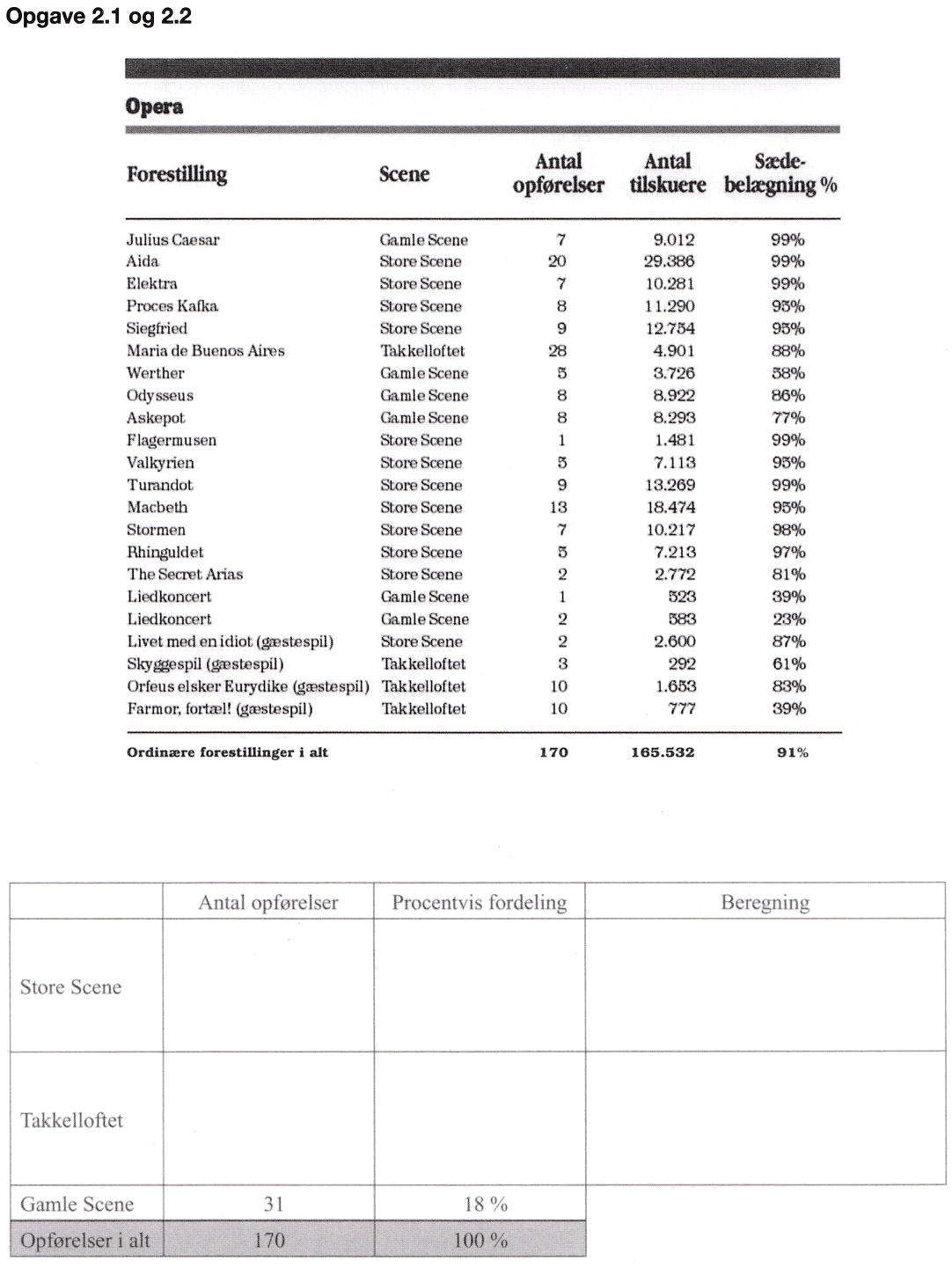
1. Antal opførelser på Stor scene: 20 + 7 + 8 + 9 + 13 + 7 + 5 + 2 + 2 = 88

   Antal opførelser på Takkelloftet: 28 + 3 + 10 + 10 = 51

2. Samlet antal operaer og koncerter er 170.

   Procentdel på stor scene: Samlet antal operaer og koncerter er 170.

   Procentdel på Stor scene = (88/170)·100 % = 51,8 %

   Procentdel på Takkelloftet = (51/170)·100 % = 30,0 %

3. Tyve gange 99 % af sæderne er lig med 29386 sæder.

   Dermed er 99 % af sæderne ved een forestilling lig med 29386/20 sæder = 1469,3 sæder.

   1 % af sæderne ved een forestilling er lig med 1469,3/99 sæder = 14,84 sæder

   100 % af sæderne ved een forestilling er lig med (14,84 sæder)·100 = 1484 sæder

4. Nedenfor er tegnet et søjlediagram med belægningsprocenterne for de forskellige forestillingsformer.

   

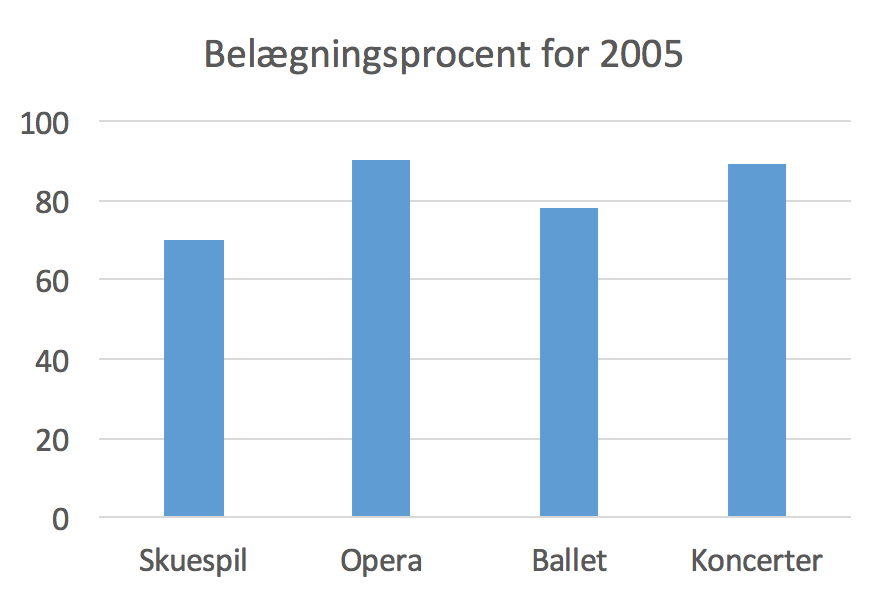
5. Diagrammet er valgt fordi, det er enkelt. Man kunne også vælge et cirkeldiagram.

Svar på opgave 3: Med klassen i operaen

1. Prisen er 2·36 kr. = 72 kr.

2. De ankommer til Nyhavn 10:56 + 5 min. 10 timer + 61 min. = 11 timer + 1 min. = 11:01.

   Den næste færgebus fra Nyhavn afgår 11:07. Denne færgebus ankommer i følge tidsplanen til operaen kl. 11:10.

   Samlet rejsetid = 11:10 - 10:56 = (11 timer + 10 min.) - (10 timer + 56 min.) = 1 time - 46 min. = 14 min.

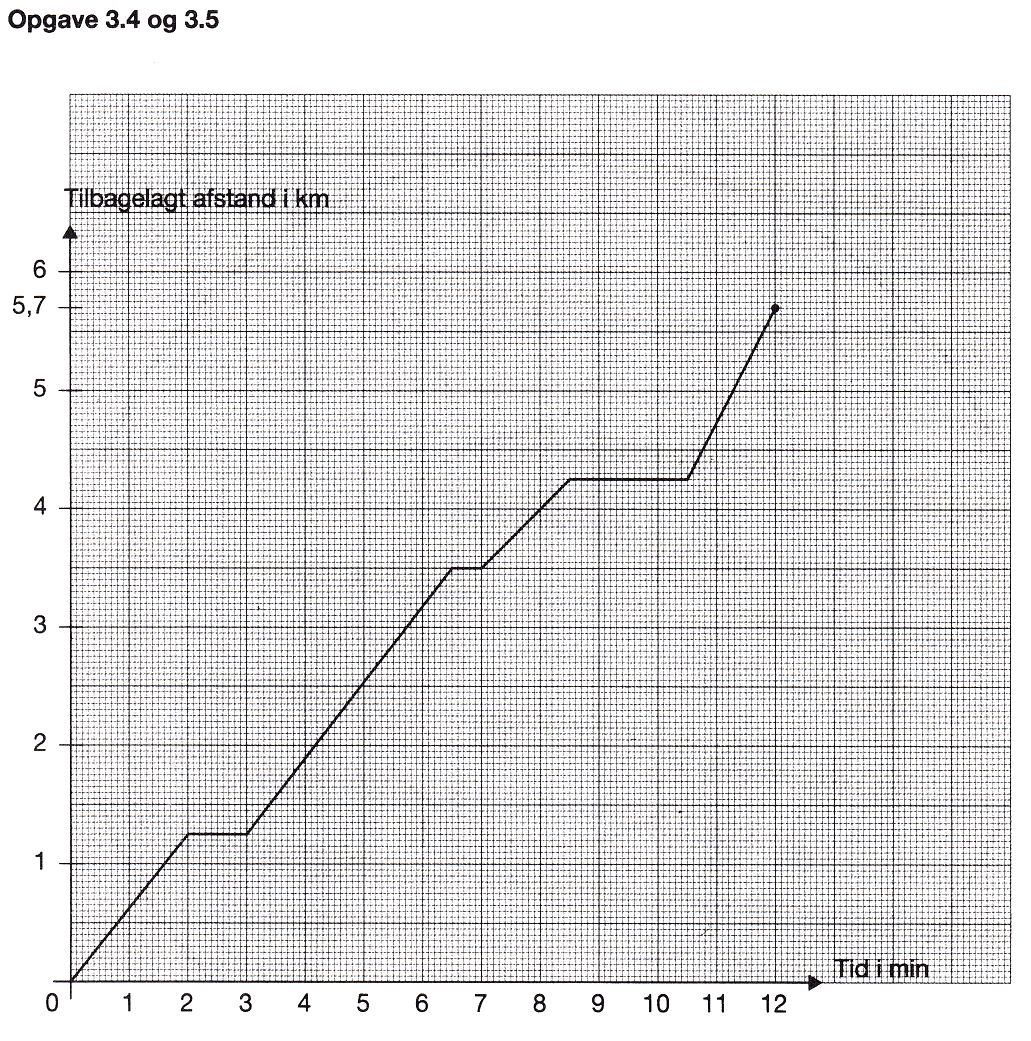
3. Gennemsnitsfarten for taxien er: (5,7 km)/(12 min.) = 0,475 km/min. = 0,475 km/(1/60 time) = 0,475·60 km/t = 28,5 km/t

   Her er farten: (5,7 km - 4,25 km)/(12 min. - 10,5 min.) = 1,45/1,5 km/min. = 0,967 km/min. = 0,967 km/(1/60 time) = 60·0,967 km/time = 58 km/t.

   Dvs. hastighedsgrænsen overskrides.

4. Farten for taxien er lig med stigningen på et stykke af grafen. Den største stigning findes mellem 10,5 min. og 12 min.

   Her er farten: (5,7 km - 4,25 km)/(12 min. - 10,5 min.) = 1,45/1,5 km/min. = 0,967 km/min. = 0,967 km/(1/60 time) = 60·0,967 km/time = 58 km/t.

   Dvs. hastighedsgrænsen overskrides.

5. Hver gang grafen er vandret holder taxien stille. Det gør den sammenlagt i: 1 min. + 0,5 min. + 2 min. = 3,5 min.

6. Pris for taxien er 19 kr. + (3,5 min.)·(6 kr./min.) + (5,7 km)·(11 kr./km) = 102,70 kr.

7. De to måder at komme frem på er næsten lige hurtige, men taxituren er dyrest.

Svar på opgave 4: Pladser i operaen

1. De skal betale for 24 elever og 2 lærere, det giver en samlet pris på: 24·40 kr. + 2·40 kr. = 1040 kr.

2. Den første kan sidde på 4 måder. For hver af disse 4 måder kan den næste sidde på 3 måder. Dette giver i alt 12 måder. For hver af disse 12, kan den tredje sidde på to måder. Dette giver i alt 24 måder. Den sidste kan kun sidde på en måde og øger dermed ikke antallet af måder.

   Dvs. de kan sidde på 24 måder

3. Brian kan sidde på 4 pladser, hvoraf de 2 er ved siden af Lis. Dette giver sandsynligheden 2/4 = 0,5 = 50 %

4. Antag af Caroline sidder på den ene side af Lis. Der er 3 sæder som Anne kan sidde på. Et sæde ved siden af Caroline og de 2 andre er ikke. Sandsynligheden for at Anne kommer til at sidde ved siden af Caroline er der for 1 ud af 3 eller 1/3 = 0,333 = 33,3 %

Svar på opgave 5: Operaens logo

1. Tegningen nedenfor er lavet i Geogebra. En tegning med de rigtige mål kræver papir.

   

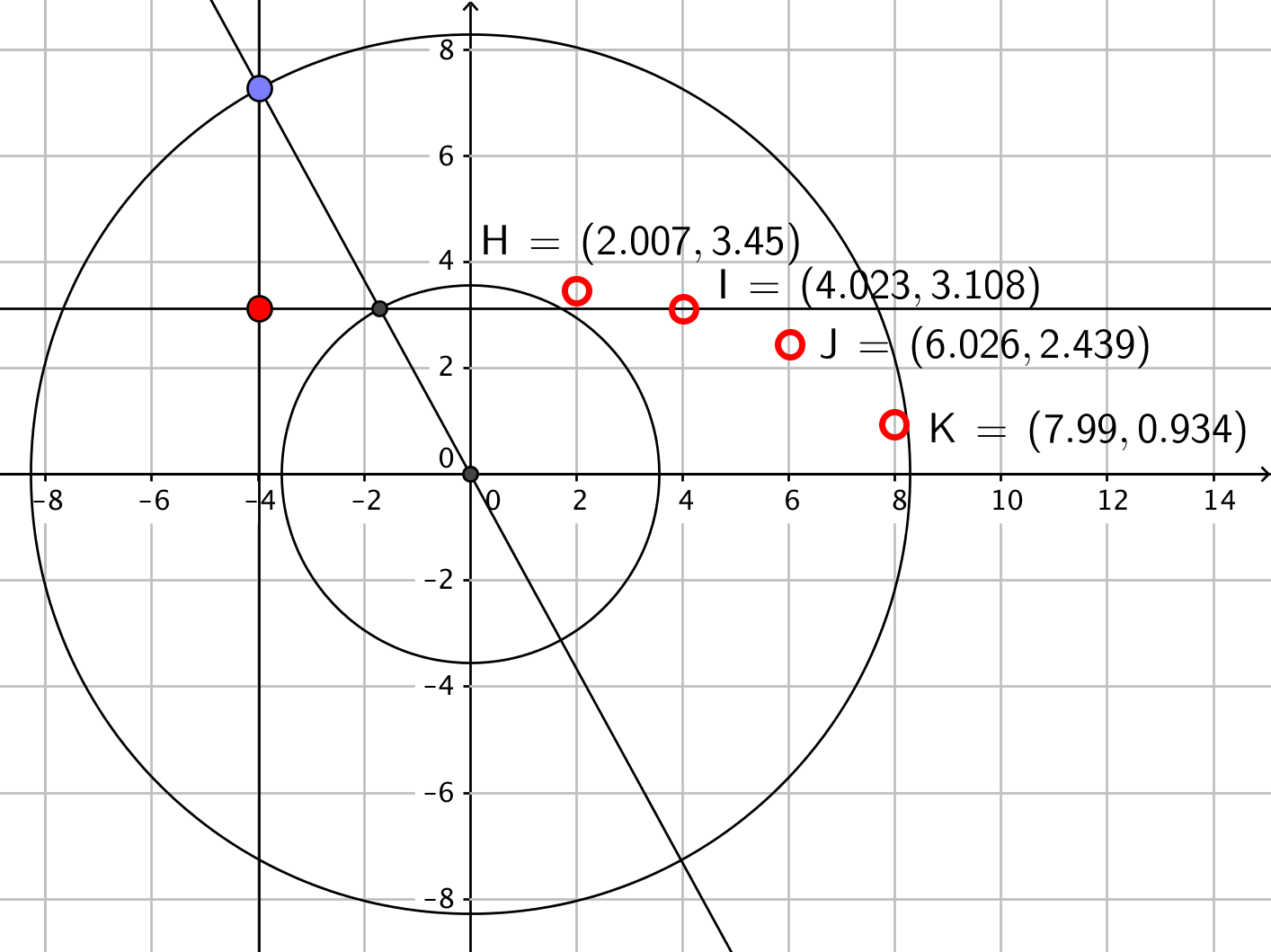
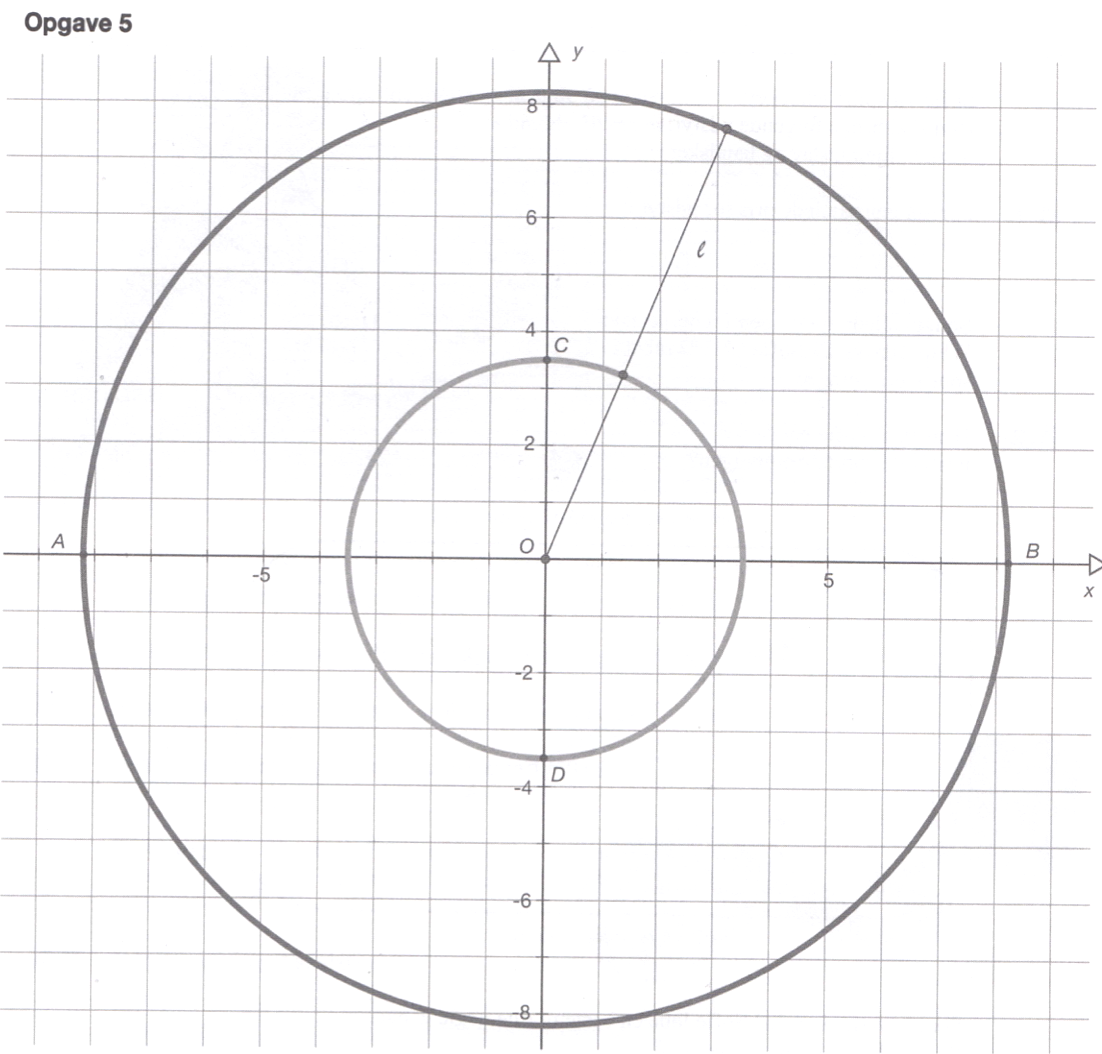
2. De fire punkter fra opgave 1 er spejlet i x-aksen og y-aksen.

   

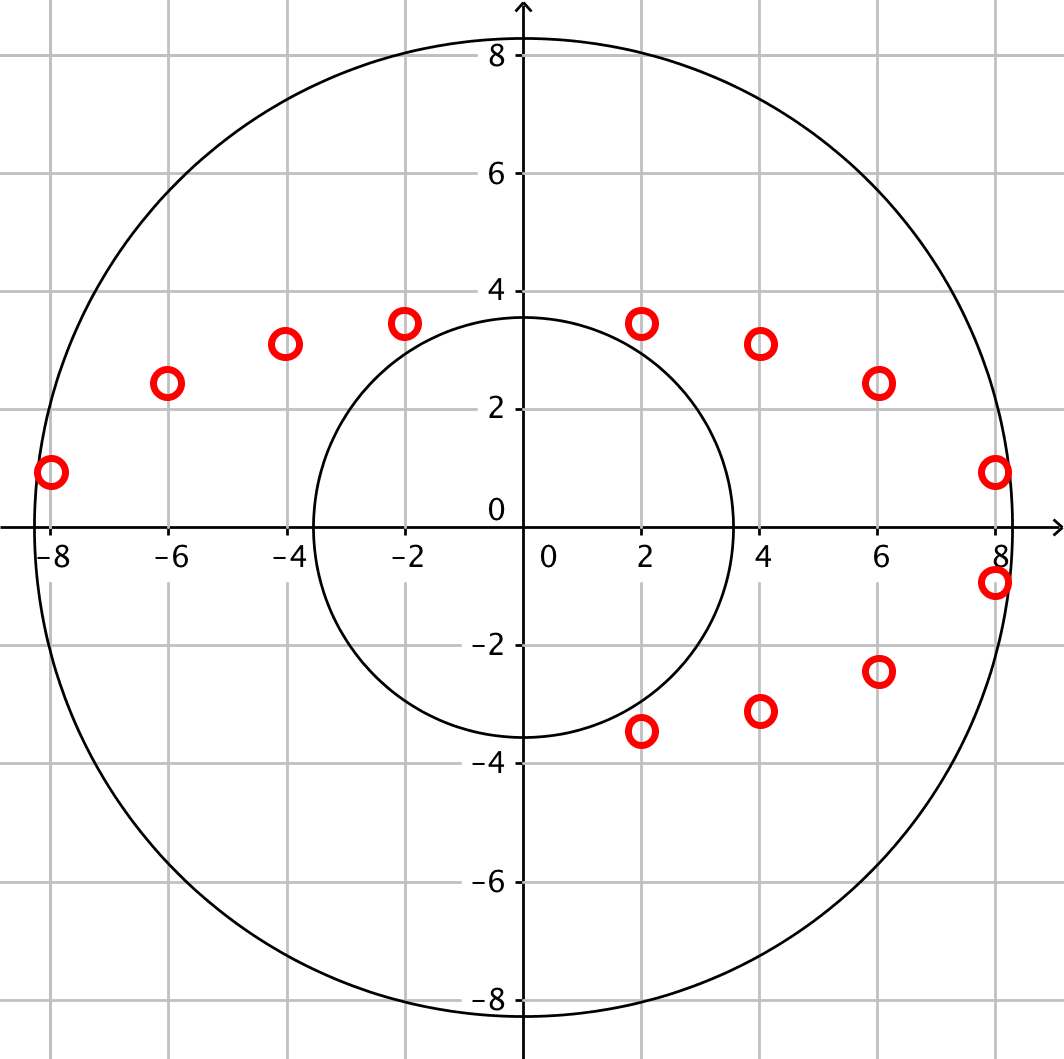
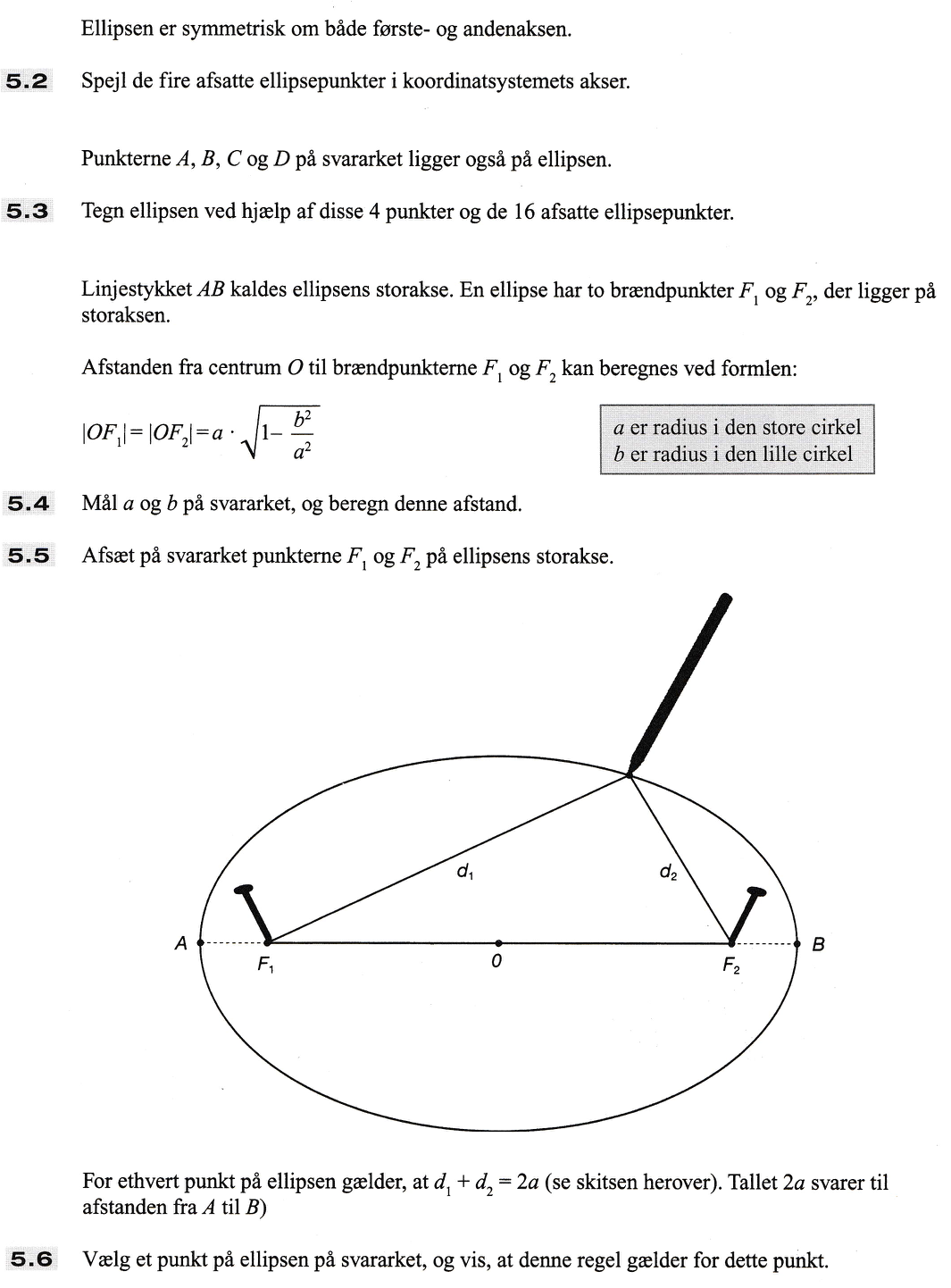
3. Ellipsen nedenunder er tegnet i Geogebra ved hjælp af fem af de viste punkter.

   

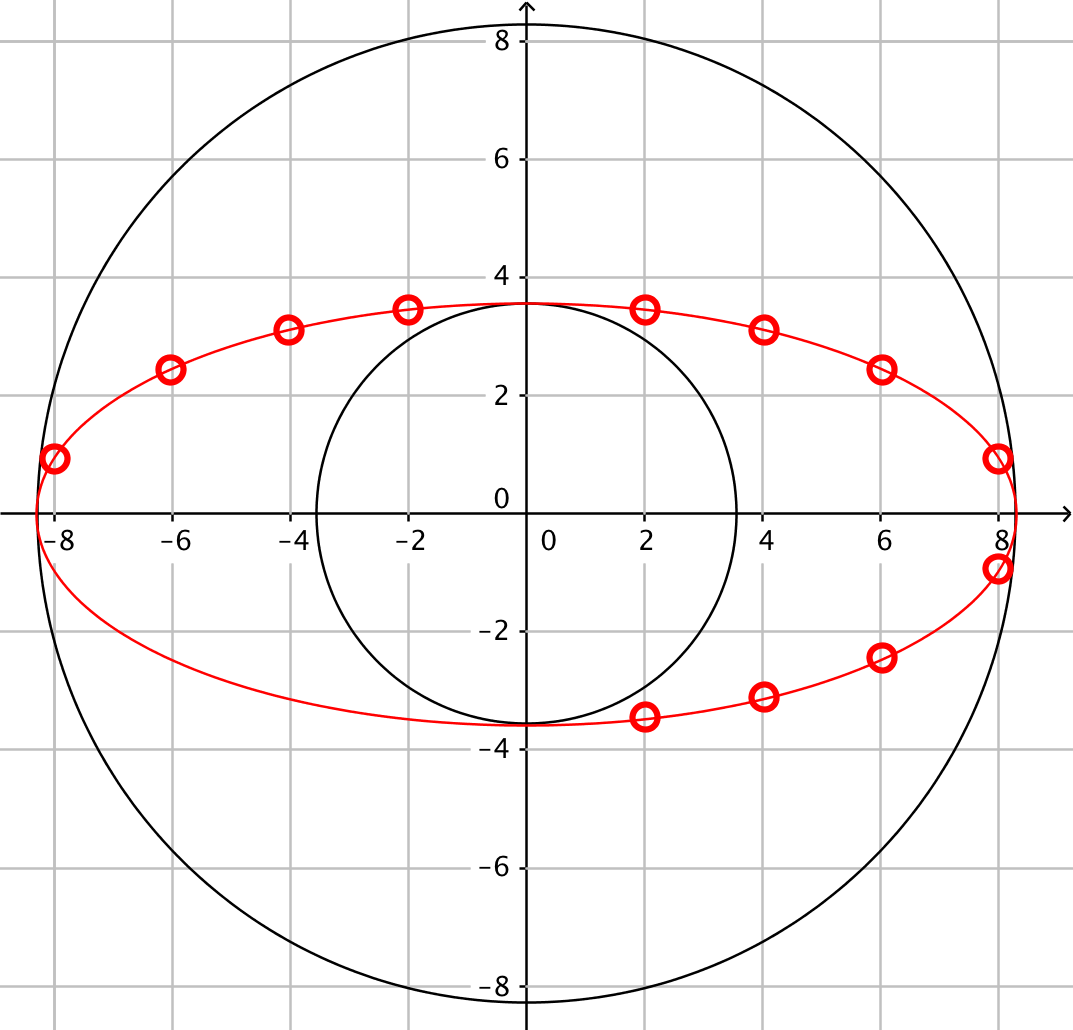
4. Tallene a og b er vist på figuren nedenunder.

   

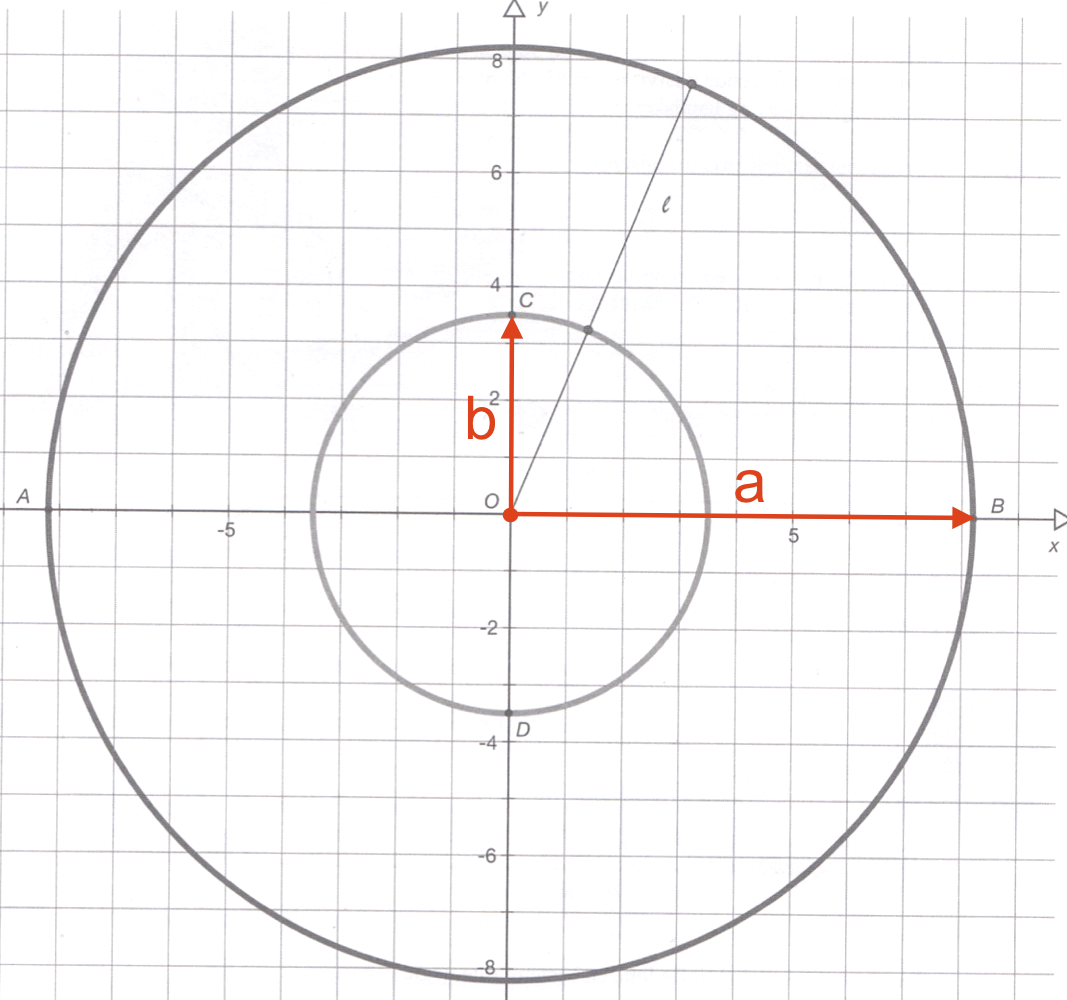
   a måles til 8,2 og b til 3,5. Dette indsættes i formlen og man får:

   for |OF₁| = 8,2·√[1 - (3,5²/8,2²)] = 7,42

5. Nedenfor er vist F₁ og F₂ som røde punkter i ellipsen. De har begge afstanden 7,4 til koordinatsystemets centrum.

   

6. Nedenfor er valgt et punkt på ellipsen i Geogebra og afstandene til brændpunkterne er målt.

   

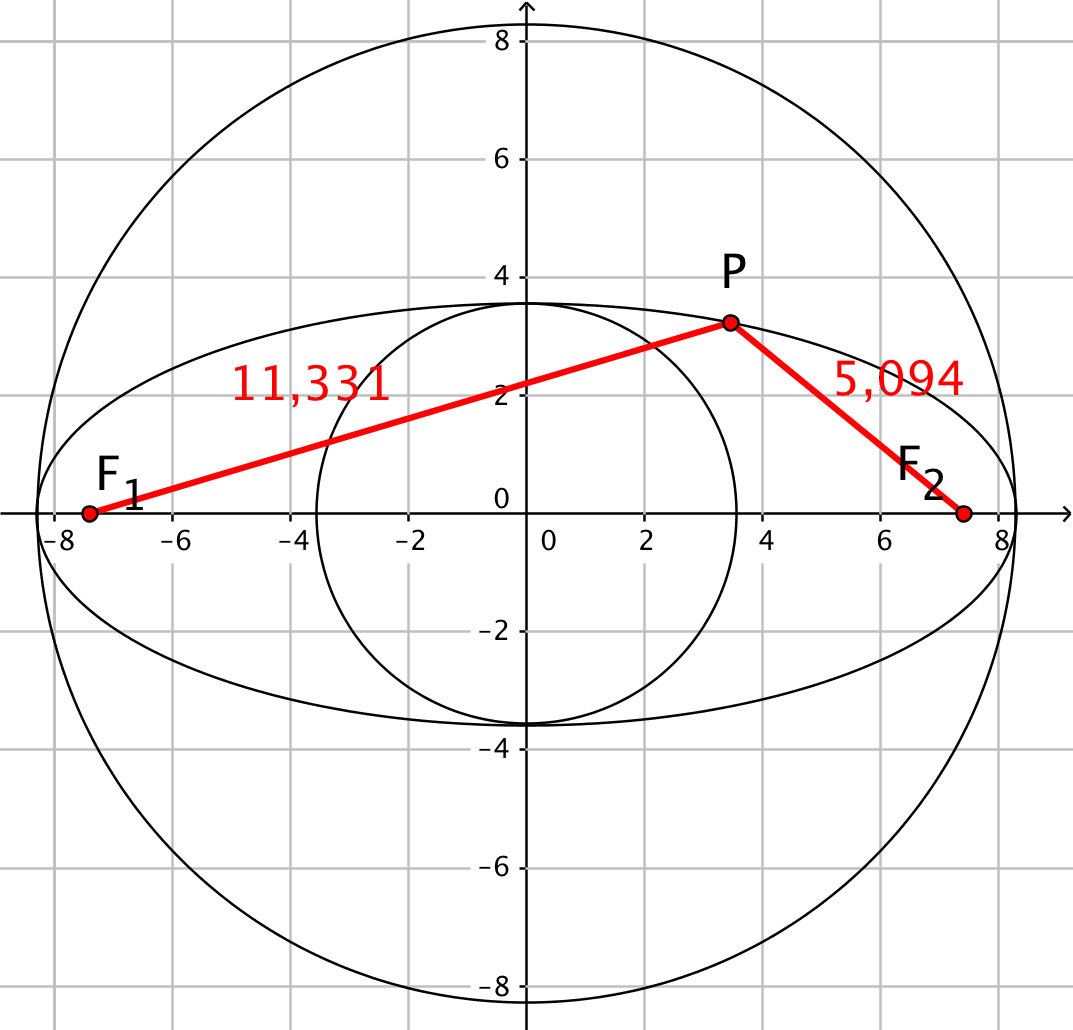
   Afstandene giver: 11,331 + 5,094 = 16,4. Dette er lig med 2 gange a = 2·8,2 = 16,4, som man skulle vise.