Man må kun anvende skriveredskab, passer, lineal og vinkelmåler. Klik på hver enkelt opgave for at se facit.
To personer køber varer, der koster 60 kr., 32 kr. og 25 kr.
1) Hvor meget koster varerne tilsammen?
2) Hvor meget betaler de hver, hvis de deler prisen ligeligt?
Svar på opgave 1:
1) (60 + 32 + 25) kr. = 117,00 kr.
2) 117/2 kr. = 58,50 kr.
En sælger får et grundbeløb på 85 kr. om dagen og 0,50 kr. for hver vare, som hun sælger.
1) Hvor meget tjener sælgeren på en dag, hvor hun sælger 150 varer?
2) Hvor mange varer har sælgeren solgt på en dag, hvor hun har tjent i alt 150 kr?
Sælgeren tjerner 90 kr. en mandag og 110 kr. en onsdag.
3) Hvor mange procent tjener sælgeren mere om onsdagen end om mandagen?
Svar på opgave 2:
1) 85,00 kr. + (0,5 kr.)·150 = 160,00 kr.
2) 85,00 kr. + (0,5 kr.)·x = 150,00 kr. ⇒ x = 130 stk.
3) (110,00 kr. - 90,00 kr.)/(90,00 kr.) = 0,222 = 22,2 % (Det som står efter "end" skal i nævneren).
En vares salgspris er 200 kr. før rabat. Der gives derefter 15 % i rabat.
1) Hvad koster varen efter rabat?
En vares salgspris er 300 kr. efter 20 % rabat.
2) Hvad kostede varen før rabat?
En vares salgspris er 60 kr. før moms. Momssatsen er 25 %.
3) Hvad er varens salgspris efter moms?
En vares salgspris er 100 kr. efter 25 % moms.
4) Hvad var salgsprisen før moms?
Købsprisen for en vare er 100 kr. Der lægges 10 % fortjeneste og derefter 25 % moms oveni.
5) Hvad er salgsprisen uden moms?
6) Hvad er salgsprisen med moms?
7) Hvor meget er momsen i kr?
Salgsprisen med 25 % moms for en vare er 150 kr.
8) Hvor meget er momsen i kr?
Svar på opgave 3:
1) (200 kr.)·(1 - 0,15) = (200 kr.)·0,85 = 170 kr.
2) (300 kr.)/(1 - 0,20) = (300 kr.)/0,80 = 375 kr.
3) (60 kr.)·(1 + 0,25) = (60 kr.)·1,25 = 75 kr.
4) (100 kr.)/(1 + 0,25) = (100 kr.)/1,25 = 80 kr.
5) (100 kr.)·(1 + 0,10) = (100 kr.)·1,10 = 110,00 kr.
6) (100 kr.)·(1 + 0,10)·(1 + 0,25) = (100 kr.)·1,10·1,25 = 137,50 kr.
7) (100 kr.)·(1 + 0,10)·0,25 = (100 kr.)·1,10·0,25 = 27,50 kr.
8) [(150 kr.)/(1 + 0,25)]·0,25 = (150/1,25)·0,25 kr. = 30,00 kr.
Bemærk at når noget gør varen billigere ved rabat, så skal procentdelen af dette (skrevet som decimaltal) trækkes fra 1. Når noget gør varen dyrere ved fortjeneste eller moms, så skal procentsatsen af disse lægges til 1. Det tal, som man får, skal så ganges med prisen, hvis man går fra før til efter og divideres op i prisen, hvis man går fra efter til før. I spørgsmål 8 gør man begge dele: Først går man tilbage til salgspris før moms, og derefter går man frem for at beregne momsen i kr.
En dreng cykler 2,5 km for at komme til skole. Det tager ham 8 minutter.
1) Hvor hurtigt kører han i gennemsnit i km/t?
2) Hvor lang ville han komme i km, hvis man cyklede med denne fart i 15 minutter?
Svar på opgave 4:
1) (2,5 km)·(60 min/t)/(8 min) = 18,8 km/t
2) (18,8 km/t)·(15/60 t) = 4,7 km
To piger deler 600 kr., så den ene får dobbelt så meget som den anden.
1) Hvor meget får de hver?
Svar på opgave 5:
1) Den, der får mindst, får beløbet x. Den, som får mest, får 2·x. Tilsammen får de beløbet: 3·x.
Dette giver følgende ligning: 3·x = 600 kr ⇔ x = 200 kr.
Dermed får den ene: 200 kr. og den anden: 2·200 kr. = 400 kr.
1) 398 - 87 = _____
2) 1076 + 2104 = _____
3) 48·17 = _____
4) 9801:9 = _____
Svar på opgave 6:
1) 398 - 87 = 311
2) 1076 + 2104 = 3180
3) 48·17 = 816
4) 9801:9 = 1089
1) 3 - (9 + 7) = _____
2) 38 + 2·(8 - 7) = _____
3) 2·102 + 76·2 + 10 = _____
4) 4,8 - 1,7 = _____
5) (1/2)·32·4 = _____
Svar på opgave 7:
1) 3 - (9 + 7) = 3 - 16 = -13
2) 38 + 2·(8 - 7) = 38 + 2·1 = 40
3) 2·102 + 76·2 + 10 = 2·100 + 152 + 10 = 362
4) 4,8 - 1,7 = 3,1
5) (1/2)·32·4 = (1/2)·3·3·4 = (1/2)·36 = 18
1) 3/8 + 1/2 = _______
2) (2/3)·(3/4) = _______
3) Skriv en uforkortelig brøk, der er dobbelt så stor som 1/3_______
4) Skriv et decimaltal, der ligger mellem 0,5 og 0,6_______
5) Skriv en brøk, der ligger mellem 1/2 og 2/3_______
6) Hvor mange procent er 40 kr. af 200 kr.?
7) Hvad er 20 % af 800 kr.?
Svar på opgave 8:
1) 3/8 + 1/2 = 3/8 + 4/8 = 7/8 (Otte er fællesnævner; det mindste tal som begge nævnere går op i).
2) (2/3)·(3/4) = 6/12 = 1/2 (Man ganger tæller med tæller og nævner med nævner. Til sidst forkortes).
3) 2/3 (1/3 gange 2)
4) 0,55 (Der er flere muligheder. Her er taget gennemsnittet: (0,50 + 0,60)/2 = 0,55)
5) 7/12 (Der er flere muligheder. Her er taget gennemsnittet: (1/2 + 2/3)/2 = 7/12)
6) 40/200 = 0,2 = 20 %. (Bemærk at ordet "af" her oversættes til et divider-tegn).
7) (20 %)·(800 kr.) = 0,20·(800 kr.) = 160 kr. (Bemærk at ordet "af" her oversættes til et gange-tegn).
En pige tager et tal, som kaldes n. Hun lægger 4 til tallet og ganger summen med sig selv.
1) Hvilken af nedenstående formler svarer til denne beregning?
a) n + 4·n + 4
b) (n + 4)2
c) (n + 4)·2
Svar på opgave 9:
1) b) (n + 4)2
Løs følgende ligninger med hensyn til x:
1) 12 - x = 10 x = ___
2) x - 8 = 2x + 1 x = ___
3) 5x + 3 = -x + 21 x = ___
4) ⅔·x - 6 = 4 x = ___
Svar på opgave 10:
1) 12 - x = 10 ⇒ x = 2
2) x - 8 = 2x + 1 ⇒ x = -9
3) 5x + 3 = -x + 21 ⇒ x = 3
4) ⅔·x - 6 = 4 ⇒ x = 15
1) 12 - x = 10 ⇒ 12 - x - 12 = 10 - 12 ⇒ -x = -2 ⇒ x = 2
2) x - 8 = 2x + 1 ⇒ x - 8 + 8 = 2x + 1 + 8 ⇒ x - 2x = 2x + 9 - 2x ⇒ -x = 9 ⇒ x = -9
3) 5x + 3 = -x + 21 ⇒ 5x + 3 - 3 = -x + 21 - 3 ⇒ 5x = -x + 18 ⇒ 5x + x = -x + 18 + x ⇒ 6x = 18 ⇒
6x/6 = 18/6 ⇒ x = 3
4) ⅔·x - 6 = 4 ⇒ ⅔·x - 6 + 6 = 4 + 6 ⇒ ⅔·x = 10 ⇒ ⅔·x·(3/2) = 10·(3/2) ⇒ x = 15
1) Hvilket udtryk svarer til beskrivelsen "x er seks mindre end y"?
1a) x = y - 6
1b) x = y + 6
1c) 2·y = x - 3
2) Hvilket udtryk svarer til beskrivelsen "x er en sjettedel af y"?
2a) x = y·6
2b) x = y/6
2c) 2·y = x·3
Svar på opgave 11:
1a) x = y - 6, svarer til "x er seks mindre end y".
1b) x = y + 6, svarer til "x er seks større end y".
1c) 2·y = x - 3, kan omskrives til x = 2·y + 3, der svarer til "x er tre større end det dobbelte af y".
2a) x = y·6, svarer til "x er seks gange større end y".
2b) x = y/6, svarer til "x er seks gange mindre end y" eller "x er en sjettedel af y".
2c) 2·y = x·3, kan omskrives til x = (2/3)·y, der svarer til "x er to tredjedele af y".
På nedenstående figur er vinklerne som vist, og sidernes længder er angivet ved hjælp af a og b:
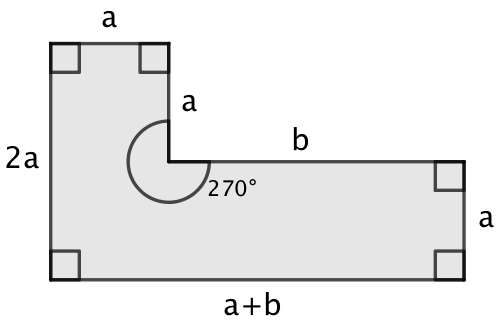
1) Hvad er omkredsen på figuren (angivet ved hjælp af a og b)?
2) Hvad er arealet af figuren?
Svar på opgave 12:
1) Omkreds: 6a + 2b
2) Areal: 2·a2 + a·b
1) 2035 g = _______kg
2) 1,35 L = _______dL
3) 3,6 t = _______kg
4) 750 m = _______km
Svar på opgave 13:
1) 2035 g = 2035·(0,001 kg) = 2,035 kg
2) 1,35 L = 1,35·(10 dL) = 13,5 dL
3) 3,6 t = 3,6·(1000 kg) = 3600 kg
4) 750 m = 750·(0,001 km) = 0,75 km
En retvinklet trekant ABC er skitseret nedenunder.
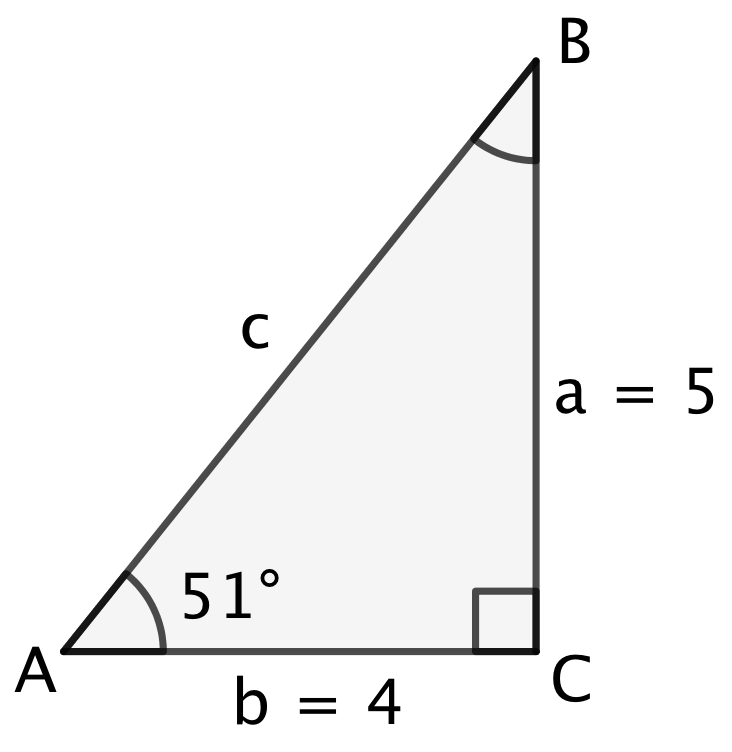
1) Hvor stor er vinkel B?
2) Hvad er trekantens areal?
3) Hvad er længden af hypotenusen c med een decimal? (Der gælder: a2 + b2 = c2)
Svar på opgave 14:
1) Summen af vinklerne er 180°. Man ved, at vinkel A er 51° og vinkel C er 90° (vist som firkant). Derfor er
vinkel B = 180° - 90° - 51° = 39°
2) Arealet er ½·a·b for den retvinklede trekant = ½·4·5 = 10
3) Hypotenusen c = √(42 + 52) = √(16 + 25) = √41 = 6,4
En cylinder er skitseret nedenunder.
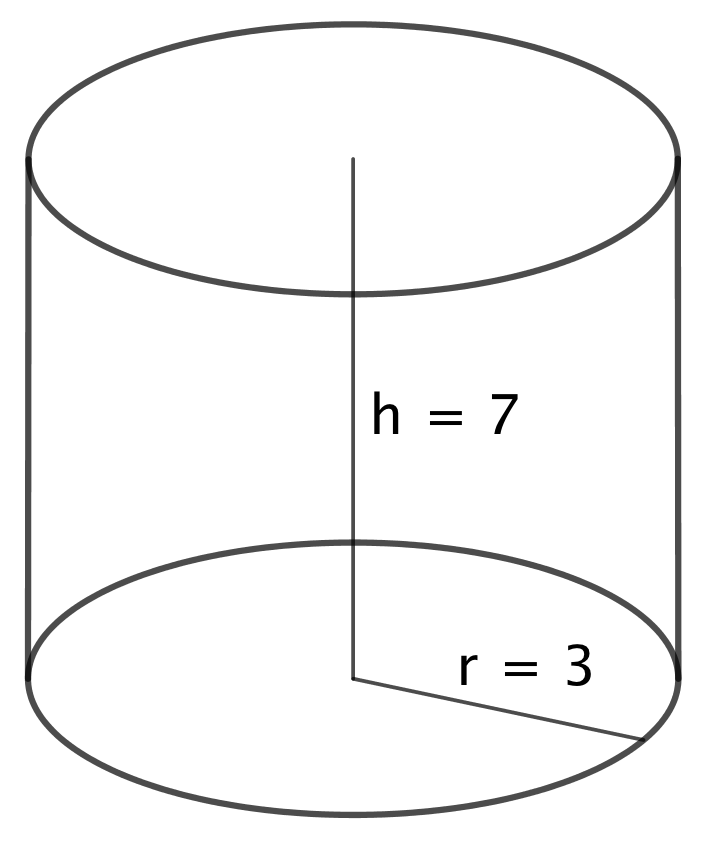
Der gælder følgende formler for cylinderen:
Rumfang = π·r2·h
Areal af krum overflade = 2·π·r·h
π kan sættes lig med 3,1.
1) Hvad er cylinderens rumfang?
2) Hvad er arealet af cylinderens krumme overflade?
Svar på opgave 15:
1) Rumfang = 3,1·32·7 = 195,3
2) Areal = 2·3,1·3·7 = 130,2
Tegningen nedenunder viser en lille og en stor terning (eller kubus).
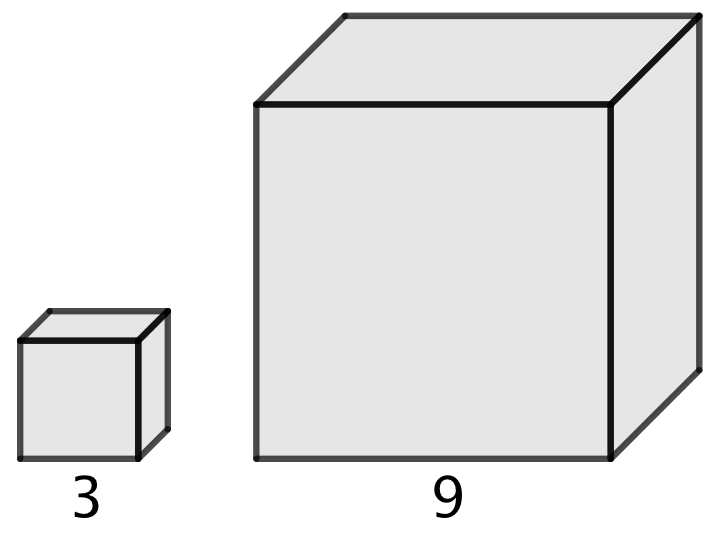
1) Hvad er forholdet mellem terningernes sidelængder?
2) Hvad er rumfanget af den lille terning?
3) Hvad er overfladearealet af den store terning?
Svar på opgave 16:
1) Forholdet er 9/3 = 3
2) Rumfanget er 33 = 27
3) Overfladearealet er 6·92 = 486
Tegningen nedenunder viser 5 forskellige trekanter kaldet A, B, C, D og E.
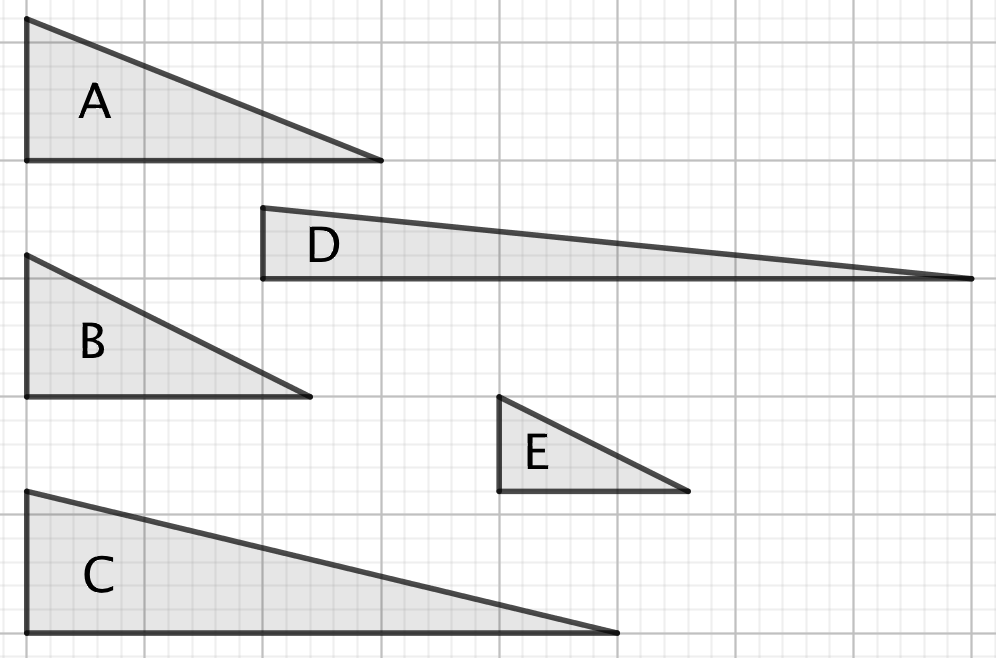
1) Hvilken trekant har samme areal som trekant A?
2) Hvilken trekant er ligedannet med trekant B?
Svar på opgave 17:
1) Trekant D. (Højden er det halve, mens grundlinjen er det dobbelte).
2) Trekant E. (Den er det halve på hver led af og dermed ligedannet med A).
Tegningen nedenunder viser to ligedannede trekanter ΔABC og ΔADE inden i hinanden. Nogle mål er vist.
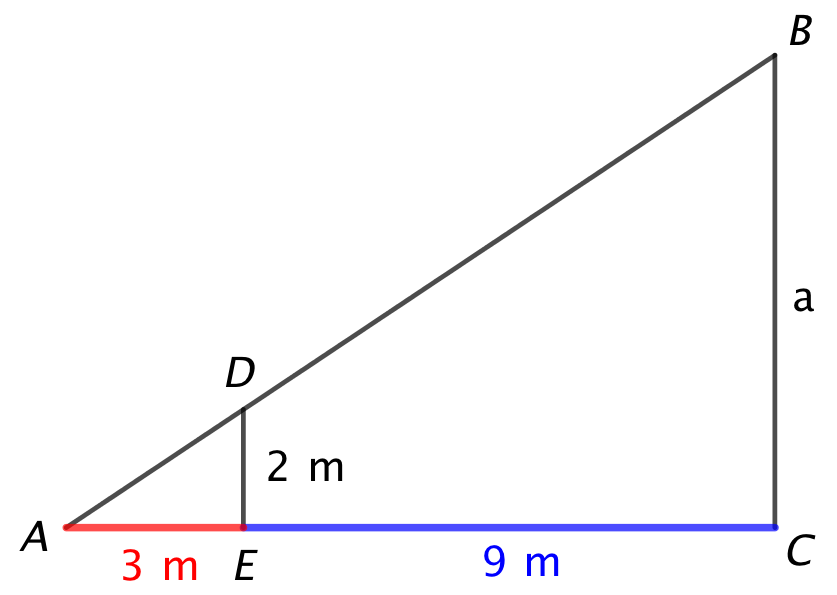
1) Find skaleringsfaktoren for de to ligedannede trekanter____
2) Find a_____
3) Hvor mange gange er ΔABC's areal større end ΔADE's?____
Svar på opgave 18:
1) 4 (Skaleringsfaktor = |AC|/|AE| = (3+9)/3 = 4. Her er det en fælde at sige 9/3=3)
2) 8 m (a/|DE| = skaleringsfaktor ⇒ a/2 = 4 ⇒ a = 8)
3) 16 gange (Forholdet mellem arealer er lig med skaleringsfaktoren i anden)
Diagrammet nedenunder viser udviklingen fra 2013 til 2016 i unges forbrug af tre tjenesteydelser.
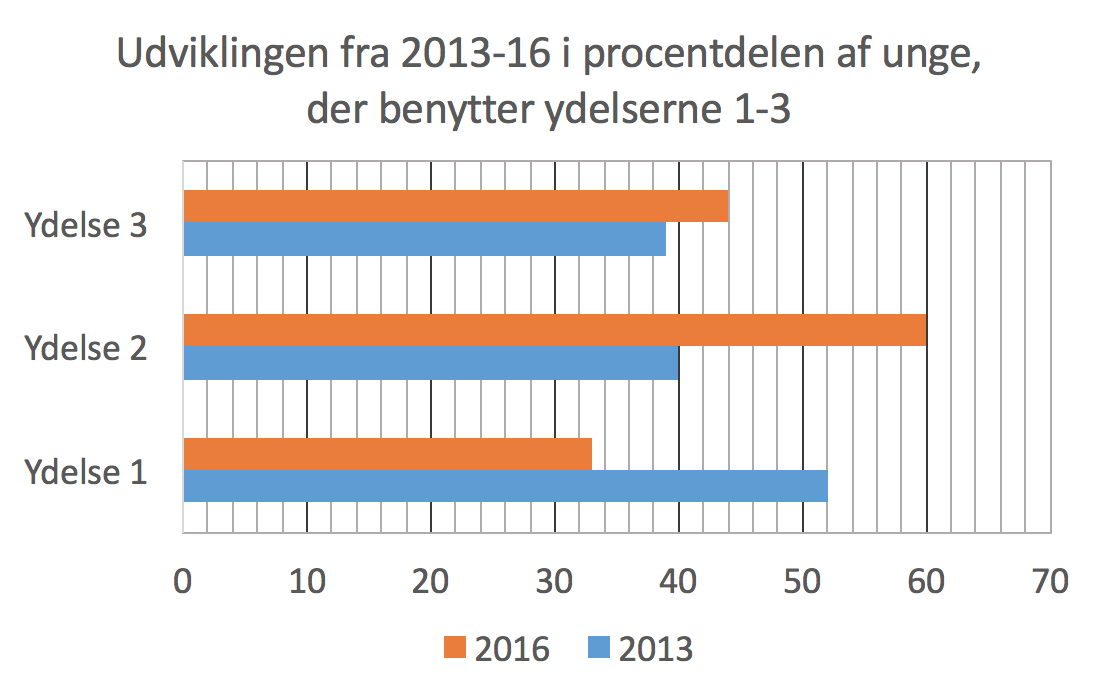
1) Hvor mange procent af de unge brugte ydelse 1 i 2013?
2) Hvor meget er andelen af unge, der bruger ydelse 2, vokset forholdsmæssigt fra 2013 til 2016?
Svar på opgave 19:
1) 52 %
2) (60 % - 40 %)/(40 %) = 0,5 = 50 % (I %-point er den vokset med 20 %-point)
Nedenstående tabel viser, hvor mange timer som 11 elever bruger på internettet dagligt. Eleverne er inddelt i syv grupper som vist.
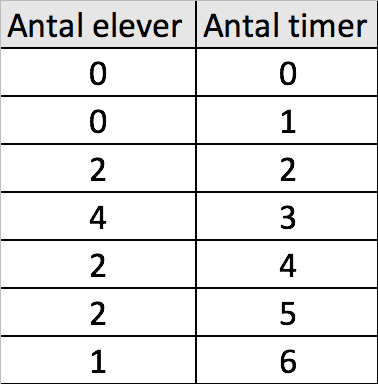
1) Hvad er det mindste antal timer, som nogen elev bruger dagligt på internettet?
2) Hvad er medianen for elevernes daglige tidsforbrug på internettet?
3) Hvad er gennemsnittet af elevernes daglige tidsforbrug på internettet?
Svar på opgave 20:
1) 2 timer. (Ingen brugte hverken 0 eller 1 time).
2) 3 timer.
(Eleverne er i tabellen ordnet efter forbrug fra mindst til størst. Man finder medianen ved at tælle fra oven i kolonnen med antal elever indtil, man når til 6, der er det midterste af tallene fra 1 til 11. Medianen aflæses så til højre).
3) (0·0 + 0·1 + 2·2 + 4·3 + 2·4 + 2·5 + 1·6)/11 timer = 3,6 timer.
En person kaster en sort og en hvid terning.
1) Hvad er sandsynligheden for, at den hvide terning viser et antal øjne, der er mindre end 3?
2) Hvad er sandsynligheden for, at den hvide terning viser et antal øjne, der er mindre end 3 samtidig med, at
den sorte viser et antal, der er større end 3?
3) Hvad er sandsynligheden for, at den hvide terning viser en sekser samtidig med, at den sorte ikke gør?
Svar på opgave 21:
1) 1/3 (Der er to antal øjne, der er mindre end 3. Der er seks mulige antal øjne i alt. 2/6 = 1/3)
2) (1/3)·(1/2) = 1/6. (Der er 1/3 sandsynlighed for, at hvid terning giver et antal øjne mindre end 3, og der er 1/2
sandsynlighed for, at sort terning giver et antal øjne, der er større end 3. Når det skal ske samtidig, så skal
sandsynlighederne ganges.)
3) (1/6)·(5/6) = 5/36. (Der er 1/6 sandsynlighed for, at hvid terning giver en sekser og 5/6 sandsynlighed for, at
sort terning giver noget andet end en sekser. Når det skal ske samtidig, så skal sandsynlighederne ganges.)