Svar på opgave 1: Julekort

1. For 500 pakker går der: 500·27,50 kr. = 13.750 kr. til julehjælp.
2. Procentdelen, der går til nødhjælp pr. pakke er: (27,50/40,00)·100 % = 68,75 %
3. Grafen er lavet i Excel og vist nedenunder.
   
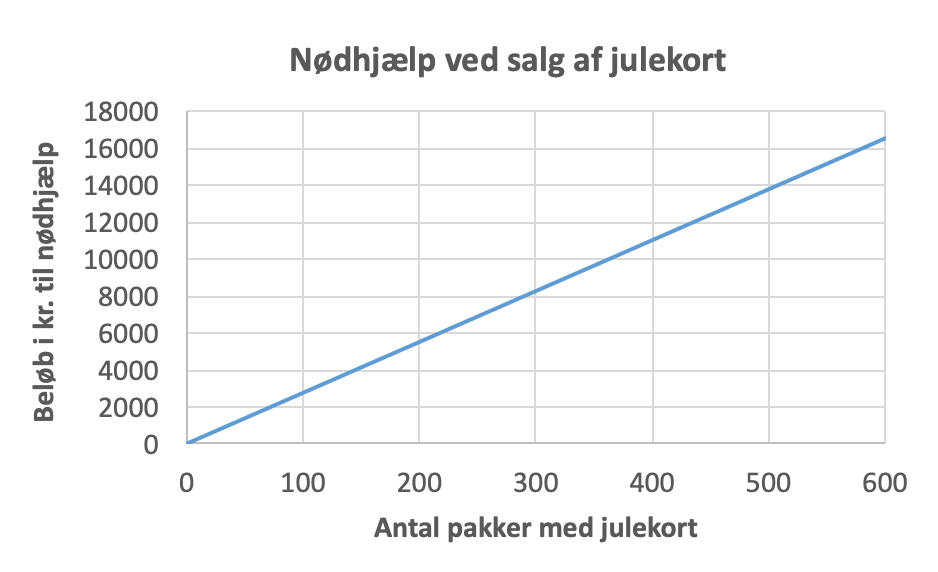
4. Virksomheden bidrager med: (750·40,00 kr.)·15 % = 4500 kr.
5. Funktionsforskriften er: f(x) = x·6, hvor x = antal solgte julekort-pakker og f(x) er virksomhedens bidrag i kr.

Svar på opgave 2: Risengrød

1. Til 4 personer skal der bruges: 4·(360 )/6 g risengrød = 240 g
2. Han skal bruge: (240 g)/((90 g)/(1 dL)) = (240/90) dL = 2,67 dL grødris.
3. Der går 4,5·(10/6) = 7,5 spiseskefulde sukker til 4 1/2 teskefulde kanel.
4. Mælk til 4 personer vejer: (2,5 L)·(4/6)·(100 g/0,97 dL) = (1,6667 L)·(100 g/0,097 L) = 1718,25 g.
   Antal gram fedt i sødmælk til risengrød for 4 personer er: (1718,25 g)·((3,5 g fedt)/(100 g)) = 60,14 g fedt.
   Antal gram fedt i letmælk til risengrød for 4 personer er: (1718,25 g)·((1,5 g fedt)/(100 g)) = 25,77 g fedt.
   Mængden af ekstra fedt i risengrød til 4 personer med sødmælk i stedet for letmælk, er: (60,14 - 25,77) g fedt = 34,4 g fedt

Svar på opgave 3: Gaveindpakning

1. Sofies gavepapir er (30 cm)·(35 cm) = 1050 cm²
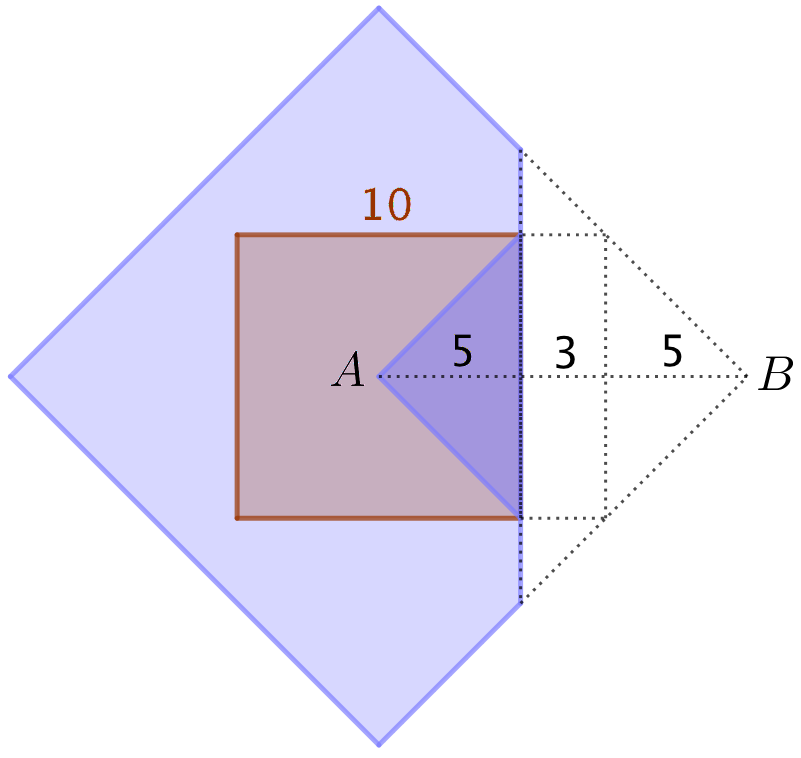
2. Midten af æsken ligger oven på midten af papiret, der kaldes A. Det ene hjørne af papiret, der kaldes B, er bukket rund om æsken. Tegningen viser papiret før og efter bukningen. For at gavepapiret skal kunne nå rundt om pakken, skal |AB| være: 5 cm + 3 cm + 5 cm = 13 cm. Hele diagonalen er 2·|AB| = 26 cm
   
3. Det fremgår af tegningen fra foregående opgave, at halvdelen af diagonalen skal være lig med æskens bredde, s, plus dens højde, h.
   Dette giver: ½·diagonal = s + h ⇔ diagonal = 2·(s + h)
4. Arealet af et kvadrat med diagonalen, d, er (d/√2)² = d²/2. Derfor er gavepapirets areal: 26²/2 cm² = 338 cm²

Svar på opgave 4: Pakkeleg

1. Sofies onkel har ikke ret. Med en ærlig terning er sandsynligheden ens for alle antal øjne.
2. Nedenstående diagram viser, at der var 1 spil ud af 100, der gav 5 seksere eller flere. Det vil sige, at 1 % simuleringerne gav mindst 5 seksere.
   
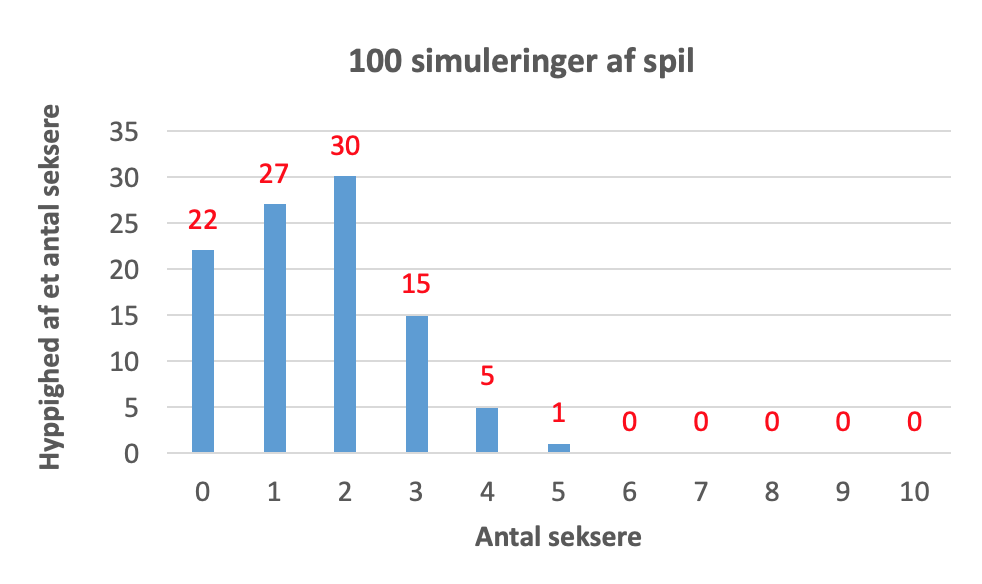
3. Sandsynligheden for at få 0 seksere i 10 kast er (5/6)¹⁰ = 0,162 = 16 %, som er mindre end 20%. Dermed har Sofie ikke ret

Svar på opgave 5: Dragefirkanter

1. Nedenfor er tegnet en dragefirkant i Geogebra med vinkler forskellge fra 90°.
   
2. Man indsætter v = 45°, a = 5 og b = 12 i formlen for at se, om man får det samme på begge sider:
   Venstre side: tan(45°/2) = tan(22,5°) = √2 - 1 = 0,414
   Højre side: a/b = 5/12 = 0,417
   Man får næsten det samme, hvilket vil sige, at v er ca. 45°.
3. Vinkelsummen i en firkant er 360°. Da v = 45°, og to af de andre vinkler er 90°, så får man, at den stumpe vinkel er: 360° - 45° - 2·90° = 135°
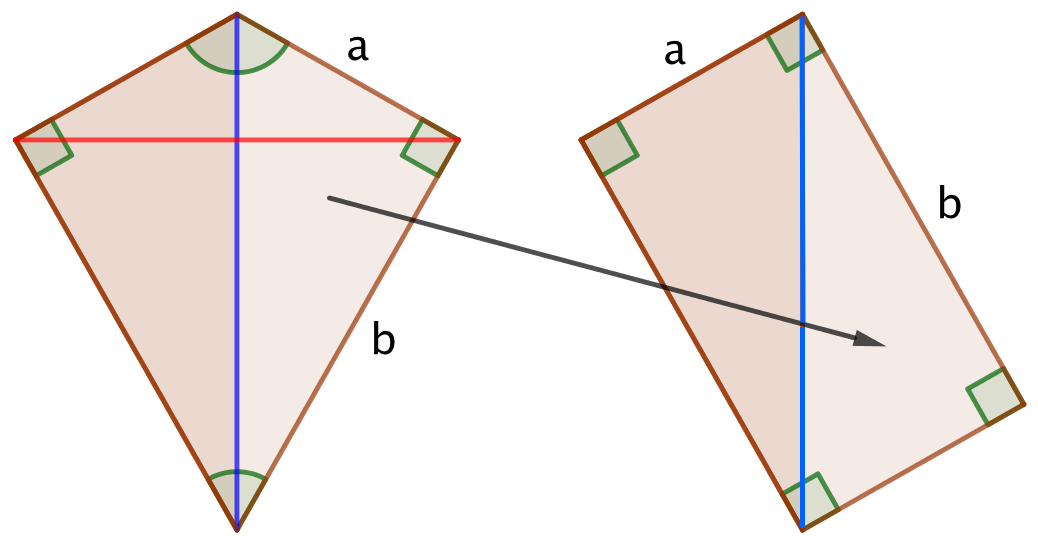
4. En dragefirkants areal er halvdelen af produktet af dens diagonaler. Dette er kun lig med produktet af den korte og den lange side, når der er tale om en dragefirkant med retvinklede hjørner som vist nedenfor.
   

Svar på opgave 6: Taltrylleri

1. Lasse får: (idet a = 10 og b = 9):
   2) 10² - 9² = 19
   3) 10 + 9 = 19
2. Man har følgende to ligninger:
   a = b + 1 og b + 1 + b = -11 ⇔
   a = b + 1 og 2b = -12 ⇔
   a = -5 og b = -6
   Det vil sige, at Lasse har valgt a som -5
3. Fordi man har valgt, at a skal være 1 større end b.
4. Når b = a - 1 gælder, at
   2) a² - b² = a² - (a - 1)² = a² - (a² - 2a + 1) = 2a - 1
   3) a + b = a + (a - 1) = 2a - 1
   Det vil sige, at man får det samme i begge tilfælde.