Svar på opgave 1: Lucas vil anlægge en terrasse

1. Terrassens areal er: (6,30 m)·(4,20 m) = 6,30·4,20 m² = 26,46 m² ≈ 26,5 m²
2. Antallet af sække kaldes x. Rumfanget af grus til terrassen er: (26,46 m²)·(0,15 m) = 3,969 m³. Der gælder, at: x·0,5 m³ = 3,969 m³ ⇔ x = 7,94.
   Det vil sige, at der skal købes 8 sække
3. Der kan være: (630 cm)/(21 cm) = 30 hele fliser på en række. Antal rækker af fliser er: (420 cm)/(14 cm) = 30. De 15 af rækkerne består af 2 halve sten og 29 hele, mens de 15 andre består af 30 hele fliser. Det giver, at der er: 15·30 + 15·29 = 885 hele fliser og 15·2 = 30 halve.
4. Det procentvise fald er: (100 %)·(2 cm)/(100 cm) = 2 %
5. Hvis Lucas mor har ret, så skal der gælde, at: 100·cos(88°) er 2. Der gælder imidlertid, at: 100·cos(88°) = 3,49 ≈ 3. Det vil sige, at Lucas mor har ikke ret!

Svar på opgave 2: Merle vil sy en stjerne

1. Antallet af romber kaldes x og man får: x·40° = 360° ⇒ x = 360°/40° = 9 gange. Det vil sige, at Merle skal bruge 9 romber til stjernen.
2. Summen af vinklerne i en firkant er 360°. Da u og v er lige store, og da de to øvrige vinkler er 40° hver, så gælder: 2·v + 2·40° = 360° ⇔ v = 140°
3. Den røde rombe kan bruges til at lave en 5-takket stjerne. (Tegnet i Geogebra).
   
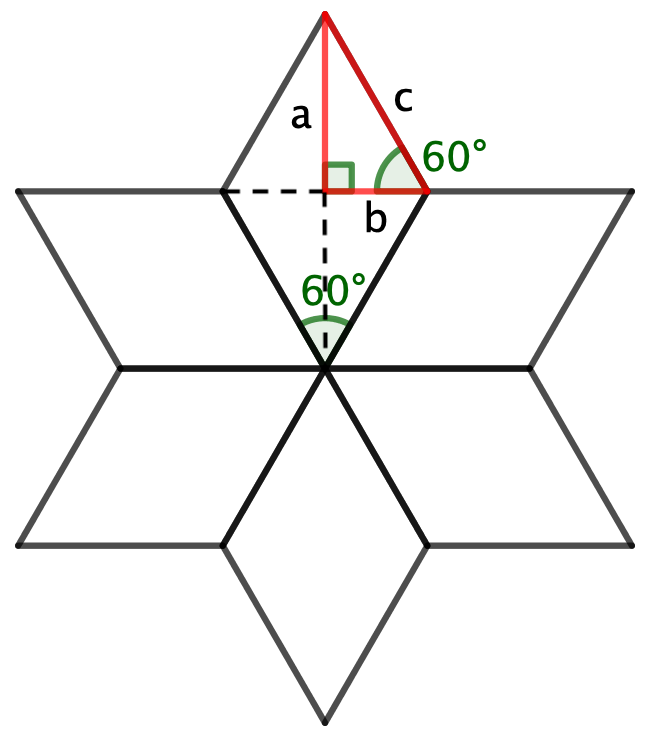
4. Nedenfor er en rombe delt i 4 ens retvinklede trekanter ved dens diagonaler. Den ene trekant er vist med rødt. Siden c er den, som man skal finde. Siden a = 10, da den er en fjerdedel af højden. Trekantens ene vinkel halverer rombens spidse vinkel på 360°/6 = 60° og er dermed 30°. Dens sidste vinkel i trekanten er 180° - 90° - 30° = 60°. For en trekant med vinklerne 30°, 60° og 90° gælder, at c = 2·a/√3. Det vil sige, at rombens sidelængde er 20/√3 cm = 11,5 cm
   

Svar på opgave 3: Clara vil fremstille æblemost

1. Clara og hendes far skal købe 100 kg æbler. Af tabellen kan man se, at 20 kg æbler koster 75 kr., og dermed koster 100 kg æbler 5 gange så meget. Det vil sige, at de skal betale 375 kr. for at lave æblemost af 96 kg æbler.
2. Clara og hendes far kan fremstille (96 kg)·(10 L)/(20 kg) = 48 L æblemost af 96 kg æbler.
3. Forholdet mellem vægten af æbler og rumfang af æblemost er 20/10 = 2. Dermed skal de bruge 2·x kg æbler til at fremstille x L æblemost.
4. Nedenunder er opgaven løst i Geogebra. Den blå trappekurve viser, hvordan prisen for at lave æblemost hos Æblelunden stiger, når man øger antallet af kg æbler. Den røde linje viser det samme for Saftpressen. Det ses, at Saftpressen er billigst, når antal kg æbler er mellem 40 og 45, og når antal kg er større end 60
   

Svar på opgave 4: Asbjørn vil så ærter

1. Sandsynligheden for at ét ærtefrø vil spire er 70 %. Heraf får man, at ud af 12 frø vil 12·(70/100) = 8,4 ≈ 8 spire.
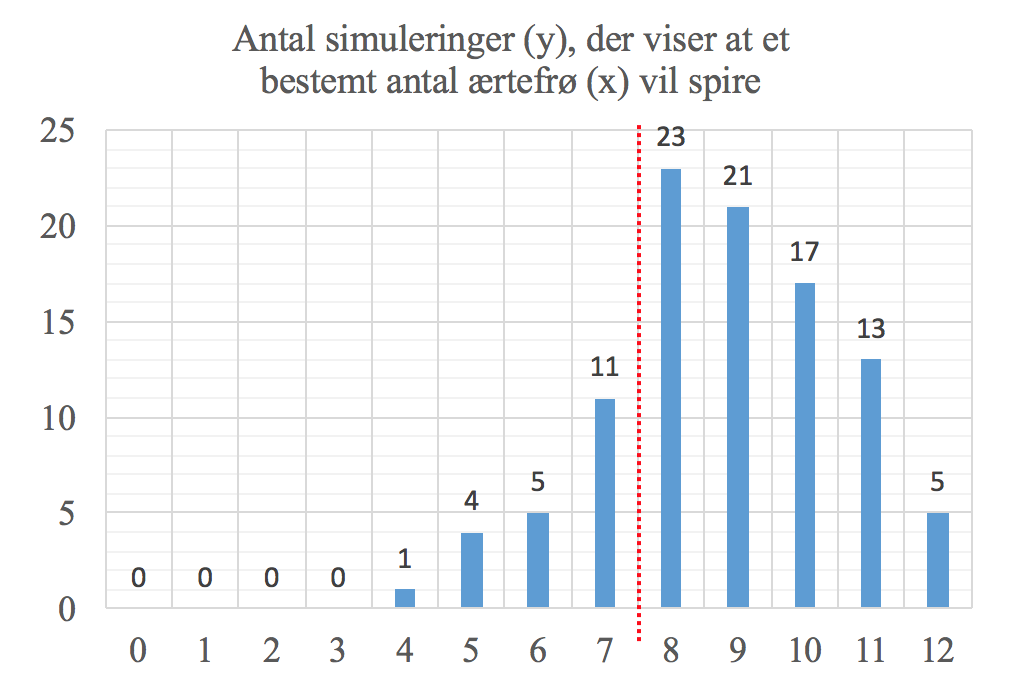
2. De simuleringer, der står til venstre for den røde linje på nedenstående figur, er de, der giver mindre end 8 spiringer. Dermed er sandsynligheden for at færre end 8 ærtefrø vil spire: (1 + 4 + 5 + 11)/100 = 0,21 = 21 %
   
3. Sandsynligheden for, at alle 12 ærter vil spire, er 0,7¹² = 0,014 = 1,4 %. Dette er mindre end 5 %.
   

Svar på opgave 5: Ligebenede trekanter

1. Et eksempel er en ligesidet trekant med alle sider lig med 6. Den har omkredsen 3·6 = 18.
2. Grundlinjen + 2·s = 18, der giver: Grundlinjen = 18 - 2s.
3. Den retvinklede trekant til højre for højden, har kateterne: h og 4 samt hypotenusen 5. Pythagoras læresætning giver: h² = 5² - 4² ⇔ h² = 9 ⇒ h = 3
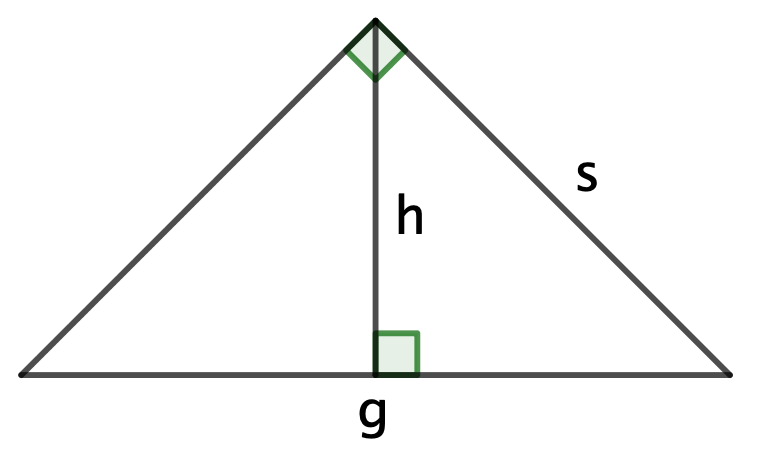
4. Man kan lave en ligebenet retvinket trekant med højden h, grundlinjen g og benlængden s. Denne er vist på nedenfor.
   Der gælder for en sådan trekant, at h = g/2, s = g/√2 og areal = g²/4.
   Trekanten skal have samme areal som figur 1, der er: 0,5·8·3 = 12.
   Heraf fås, at g²/4 = 12 ⇔ g = 4√3, h = 2√3 og s = 2√6. Disse sidelængder er alle forskellige fra figur 1's.
   

Svar på opgave 6: Trappefigurer

1. Trappefiguren er vist nedenunder:
   
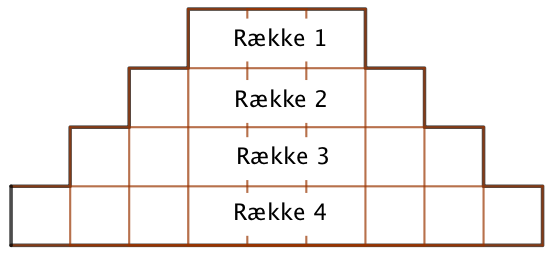
2. En trappefigur med 10 rækker og 1 kvadrat i række 1, vil i følge formlen have: 10² kvadrater = 100 kvadrater
3. En trappefigur med 2 kvadrater i række 1 svarer til en trappefigur med 1 kvadrat i række 1, hvor man lægger et ekstra kvadrat til i hver række. Dette er vist nedenunder. Formlen bliver: K₂ = r² + r
   
4. Man skal finde K_n, når n = 10 og r = 100. Dette antal er 100·(100 - 1 + 10) = 10900
5. K_n = r·(r - 1 + n) =
   r² - r·1 + r·n =
   r·n - r·1 + r² =
   r·(n - 1) + r²