Svar på opgave 1: I svømmehallen

1. Astrid skal have følgende beløb tilbage: 200 kr. - 2·(46 kr.) = (200 - 92) kr. = 108 kr.
2. Antallet af gange, som Victor går i svømmehallen, kaldes x. Den årlige pris for x ture i svømmehallen er x·(46 kr.). Dette beløb må ikke være større end 900 kr.
   Det x, som gør de to beløb lige store, findes af følgende ligning: 900 kr. = x·(46 kr.) ⇔ (900 kr.)/(46 kr.) = x ⇔ x = 900/46 gange ⇔ x = 19,6 gange.
   Det vil sige, at hvis han går 20 gange i svømmehallen eller mere, kan det bedst betale sig for ham at købe et årskort.
3. Den procentvise besparelse ved at bruge et ti-turskort frem for ti enkeltbiletter er:
   (100 %)·[(10·46 kr.) - (375 kr.)]/(10·46 kr.) =
   (100 %)·(85 kr.)/(460 kr.) = 18,48 % ≈ 18 %
   Det vil sige, at oplysningen er rigtig, når man runder af til et helt tal.
4. x ti-turskort koster x·375 kr. Dette sættes lig med prisen på et årskort, som er 900 kr.:
   x·375 kr. = 900 kr ⇔ x = 900/375 ti-turskort ⇔ x = 2,4 ti-turskort.
   Det rundes op til 3 ti-turskort, der svarer til mellem 21 og 30 besøg i svømmehallen.
   De skal derfor gå mindst 21 gange i svømmehallen før et årskort er billigere end at bruge ti-turskort.

Svar på opgave 2: Regnvandstank

1. Areal = 2·(10,1 m)·(5,9 m) ≈ 119 m²
2. Tangens til v er lig med (3,8m)/(4,5m) = 0,8444, hvilket giver, at v = tan^-1(0,8444) = 40°.
3. I følge modellen er vandforbruget: 119·(40/360 + 0,6)·900 L = 78.540 L
4. En cyliderformet tank har rumfanget:
   (1,8m)·(1,6m/2)²·π =
   (1,8·0,64·π) m³ =
   3,61911 m³ = 3619 L.
   Det passer, at den kan rumme 3500 L.
5. Rumfanget af hullet er i følge formlen: (1/3)·π·(1,8 m)·((4,3/2)²+(1,6/2)²+(4,3/2)·(1,6/2)) = 13,2 m³

Svar på opgave 3: Vandforbrug i brusebadet

1. Vandforbruget er (14 L/min.)·(8,5 min.) = 119 L
2. Prisen for et fem minutters brusebad er (5 min.)·(14 L/min.)·(0,10 kr./L) = 7,0 kr.
3. Funktionsforskriften er 7·n kr.
4. Prisen for et bad, der varer i x minutter, er x·(8 L/min.)·(0,10 kr./L) = x·0,8 kr. Dette skal være lig med 7,0 kr. Man får ligningen: x·0,8 = 7,0 ⇔ x = 8,75.
   Det vil sige, at hun kan tage bad i 8 min. 45 sek. for 7,0 kr. med den nye bruser.
5. Et bad på 5 minutter koster 7,0 kr. med den gamle bruser. Med den nye bruser koster et bad på 5 minutter: (5 min.)·(8 L/min.)·(0,10 kr./L) = 4,0 kr.
   Besparelsen pr. bad er (7,0 - 4,0) kr. = 3,0 kr. Den nye bruser koster 995 kr. Antallet af bade er: 995 kr./3 kr. = 332 før den nye bruser er tjent hjem.

Svar på opgave 4: Vandforbrug i en boligforening

1. Forbrug af vand:
   Nyvej 3: (82 + 51 + 144 + 84 + 120 + 148 + 148 + 108 + 160 + 86) m³ = 1131 m³
   Nyvej 5: (144 + 153 + 93 + 130 + 150 + 108 + 54 + 150 + 145 +57) m³ = 1184 m³
   Det vil sige, at der bliver brugt mest vand på Nyvej 5
2. 1 m³ = 1000 L. Viktors familie bruger i gennemsnit: (144 m³/365 dage) = 395 L/dag
3. Median:
   Nyvej 3: (37+40)/2 = 77/2 = 38,5
   Nyvej 5: (31+36)/2 = 67/2 = 33,5
   Variationsbredde:
   Nyvej 3: 51 - 32 = 19
   Nyvej 5: 57 - 25 = 32
   Middeltal:
   Nyvej 3: (32+36+36+37+37+40+41+42+43+51)/10 = 39,5
   Nyvej 5: (25+26+29+30+31+36+51+54+54+57)/10 = 39,3
   Konklusion: Medianen for Nyvej 3 er større end for Nyvej 5. Middeltallene er derimod næsten ens, hvilket kan forklares ved at nogle få lejligheder på Nyvej 5 har et meget stort forbrug, der trækker middeltallet op i forhold til medianen. Det sidste passer også med, at Variationsbredden er større for Nyvej 5 i forhold til for Nyvej 3.
4. Man kan regne ud hvor mange personer, der er i hver lejlighed, ved at dividere det gennemsnitlige forbrug pr. person op i det samlede vandforbrug for lejligheden. Dernæst sorterer man lejlighederne efter antal personer. For hver gruppe af lejligheder med samme antal personer regner man det gennemsnitlige vandforbrug pr. person ud:
   
   Ud fra tabellen kan man lave følgende kurve i Geogebra:
   
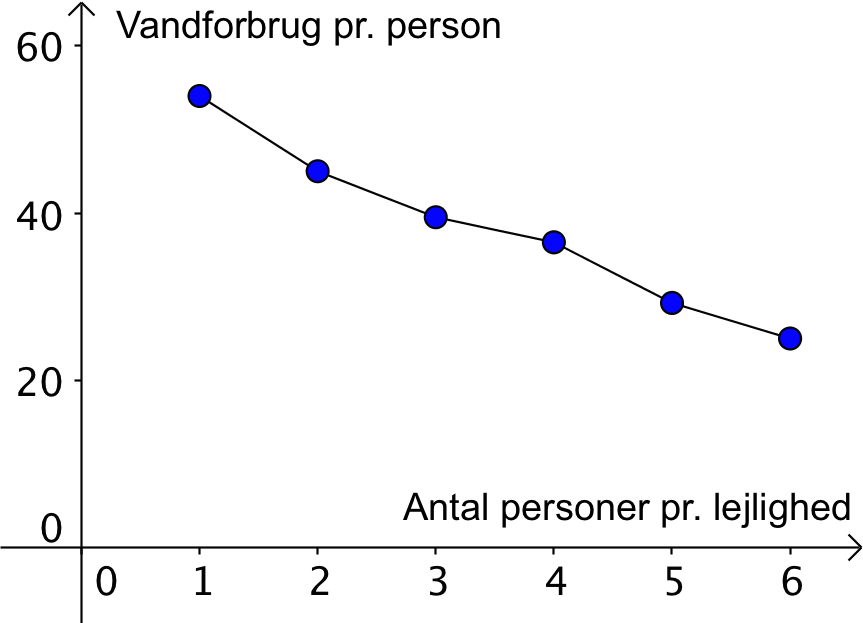
   Kurven viser at jo flere, der bor i en lejlighed, jo mindre vand bruger den enkelte.

Svar på opgave 5: Firkanter i trekanter

1. Nedenfor er tegnet en trekant med en firkant i Geogebra.
   
2. Vinklen v indgår i en retvinklet trekant, som er vist med blåt på nedenstående tegning. Da den røde firkant er et kvadrat, så er alle dens sider lige lange, og da dens ene af dens sider deler den nederste side i trekanten i tre lige store stykker er den blå trekant ligebenet. Da v er grundvinklen i en ligebenet retvinklet trekant, så er v = 45°
   
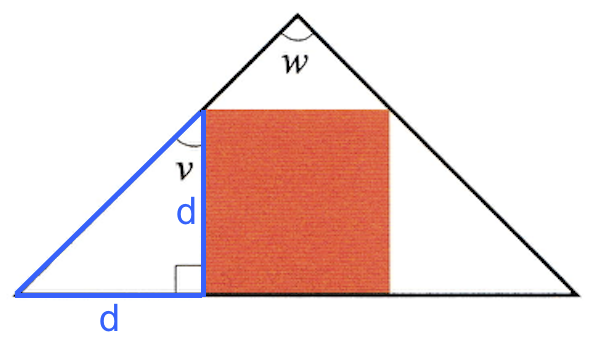
3. Man kan vise, at de to vinkler forneden i den store trekant er 45° på grund af symmetri omkring en linje midt gennem kvadratet. Dermed er w lig med 90° i følge reglen om, at vinkelsummen i en trekant er 180°.
   
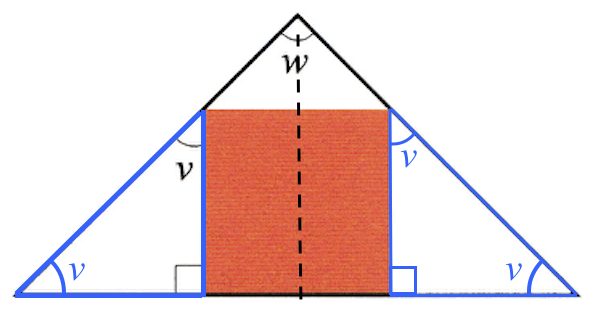
4. På nedenstående tegning er vinkler med samme farve lige store. Man har, at ∠C = 180° - (∠A + ∠E). Man skal vise, at ∠A + ∠E = 90°.
   Det ses, at ΔABG og ΔDEF begge er ligebenede. Dermed er ∠A = 90° - (1/2)·∠AGB og ∠E = 90° - (1/2)·∠DFE. Det fremgår desuden, at ∠AGB + ∠DFE = 180°.
   Det giver tilsammen:
   ∠A + ∠E = (1/2)·[(180° - ∠AGB) + 180° - ∠DFE] ⇔
   ∠A + ∠E = (1/2)·[360° - (∠AGB + ∠DFE)] ⇔
   ∠A + ∠E = (1/2)·[360° - 180°] ⇔
   ∠A + ∠E = 90°
   Dermed er vinkel C = 180° - 90° = 90°, hvilket skulle bevises.
   

Svar på opgave 6: Sumfigurer

1. Sumfiguren er vist nedenunder:
   
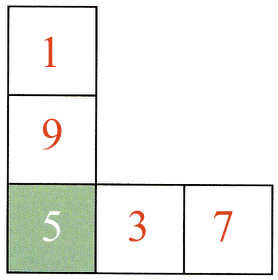
2. De lige tal: 4, 6 og 8 kan stå der. Hvis der står et ulige tal i det grønne felt, så vil der komme til at stå et lige og et ulige tal i to af de hvide felter, mens der står to lige i de to andre. Dette kan ikke give samme sum.
3. Der gælder ligningen:
   2n + 1 + 5n + 8 = 10n - 3 + n + 4 ⇔
   7n - 11n = 1 - 9 ⇔
   n = 8/4 = 2
4. Man har ligningerne:
   2n + m + 5 = 15 ∧ 5 + 3m + n = 15 ⇔
   m = 10 - 2n ∧ 5 + 3·(10 - 2n) + n = 15 ⇔
   m = 10 - 2·4 ∧ n = 4 ⇔
   m = 2 ∧ n = 4
5. Man får den største sum, hvis n + 4 står i det grønne felt. Summen af alle felter er n + (n + 1) + (n + 2) + (n + 3) + (n + 4) = 5n + 10. Tallet i det grønne felt kaldes x. Summen vandret = x + (5n + 10 - x)/2 = (1/2)·x + (5/2)·n + 5. Dette viser, at jo større tallet i det grønne felt er, jo større er den vandrette og dermed også den lodrette sum.