Svar på opgave 1: Ferielejlighed i Italien

1. Forskellen på udlejningsprisen for 7 og 14 dage er (10.617 - 7.566) kr. = 3051 kr.
2. Familien består af fire personer. Den samlede regning er derfor: 10.617 kr. + 4·130 kr. + 625 kr. = 11.762 kr.
3. Den samlede pris med 12 % rabat er: (11.762 kr.)·(100 % - 12 %) = (11.762 kr)·0,88 = 10.351 kr.
4. Prisen bliver den samme uanset den rækkefølge, som man tager rabatten i.
   Prisen for først 12 % rabat og dernæst 3 % er: (11.762 kr)·(100 % - 12 %)·(100 % - 3 %) = (11.762 kr)·(0,88)·(0,97) = 10.040 kr.
   Prisen for først 3 % rabat og dernæst 12 % er: (11.762 kr)·(100 % - 3 %)·(100 % - 12 %) = (11.762 kr)·(0,97)·(0,88) = 10.040 kr.

Svar på opgave 2: Danskernes mest populære feriemål

1. Af figuren i opgaven ses, at 15 % de ferierejsende danskere tager til Spanien og 10 % tager til Italien. Dette giver tilsammen, at 25 % af de danske ferierejsende tager til enten Spanien eller Italien.
2. Det samlede antal rejsende kaldes a. Antal rejsende til Spanien = a·15 % og antal rejsende til Italien = a·10 %. Den procentvise forskel er :
   (a·15 % - a·10 %)/(a·10 %) = (15 - 10)/10 = 0,5 = 0,5·100 % = 50 %
3. Det mindste procentdel af de rejsende, der tog til Spanien, er (15 % - 2 %) = 13 %. Derfor er det mindste antal rejsende (4,8 mio.)·13 % = 624.000
4. Man kan ikke være sikker på, at Italien er det næst mest besøgt feriemål, fordi den procentdel, der rejser til Italien kan være (10 % - 2 %) = 8 %. Samtidig kan Tysklands andel af turistrejser være (8 % + 2 %) = 10 %. Dermed kan Tyskland godt være mere besøgt end Italien.

Svar på opgave 3: Peterspladsen i Rom

1. Nedenunder er ovalen tegnet i Geogebra.
   
2. Et rødt linjestykke går fra et punkt på cirkelperiferien, gennem centrum og ud til det modsat-stående punkt på periferien. Dermed er et rødt linjestykke en diameter til cirklen. Radius er derfor det halve af 30, nemlig 15
3. Nedenfor er vist en blå trekant, der forbinder de to centre med hinanden og hvert center med toppunktet for vinklen u. Alle sider i denne trekant er lig med radius, og dermed er trekanten ligesidet. Heraf følger, at u er 60°. På samme måde ses, at v også er 60°.
   
4. Nedenfor er vist, at den røde cirkelbue har radius 30. Desuden spænder buen over vinklen u, som er 60°. Dermed er cirkelbuen en sjettedel af omkredsen af en cirkel med radius 30, og den har derfor længden: (1/6)·2·π·30 = 10·π.
   
5. På figuren nedenunder har den blå bue længden: (120°/360°)·2·π·15 = 10·π. Dermed er røde og blå buer lige lange og ovalens omkreds er derfor: 4·10 π = 40 π
   

Svar på opgave 4: Leje af cykler

1. Leje af en cykel i 7 dage koster: 7·12 € + 5 € + 7 € = 96 €
2. Udtrykket for prisen i € af leje af cykel med udstyr i n dage er: n·12 + 5 + 7 = 12·(n + 1)
3. Prisen i € for 2 personer i n dage er 2·12·(n + 1) = 24·(n + 1). Antallet af €, som de har, er: (1500 kr.)/(7,50 kr.) = 200. Man skal finde n i ligningen:
   24·(n + 1) = 200 ⇔
   n = 200/24 - 1 ⇔
   n = 7,33
   Det vil sige, at de har råd til 7 dage
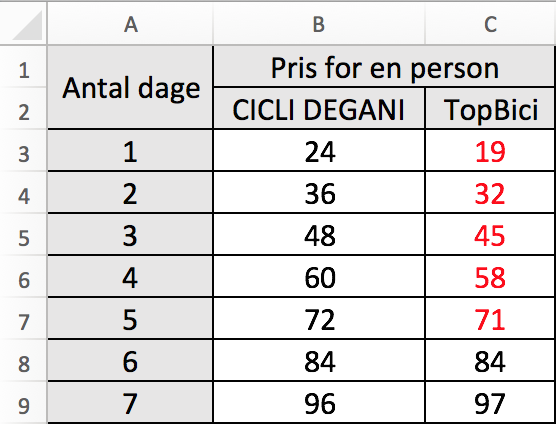
4. Nedenunder er vist en tabel lavet i Excel over priser for leje af cykel for en person i de to udlejnings­firmaer. De røde tal viser, hvornår TopBici er billigst. Det ses, at TopBici er billigst, hvis man højst lejer en cykel i 5 dage
   

Svar på opgave 5: Femkantede fliser

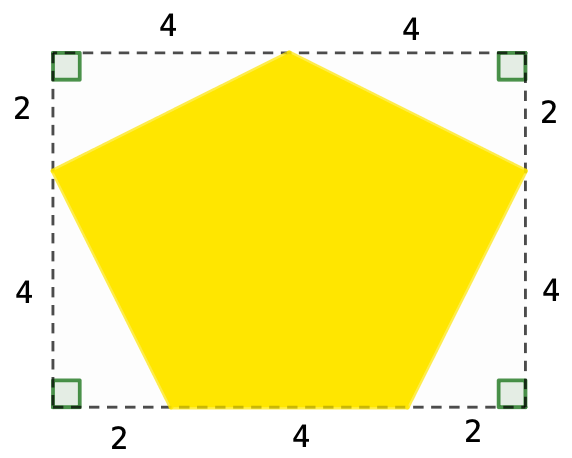
1. Nedenunder er femkanten tegnet i Geogebra.
   
2. Som vist nedenfor, så er arealet af femkanten lig med arealet af den sorte rektangel minus arealet af de fire ens retvinklede trekanter. Rektanglets areal er (4 + 4)·(2 + 4) = 6·8 = 48. De retvinklede trekanters areal er 4·(0,5·4·2) = 16. Det vil sige, at arealet af femkanten er 48 - 16 = 32
   
3. Femkantens har fire skrå kanter, som er hypotenuser i de ovennævnte retvinklede trekanter samt en kant forneden, som har længden 8 - (2 + 2) = 4. Hypotenusernes længde findes ved hjælp af Pythagoras læresætning til √[2² + 4²] = √20. Det vil sige, at omkredsen af femkanten er 4 + 4·√20 ≈ 21,9
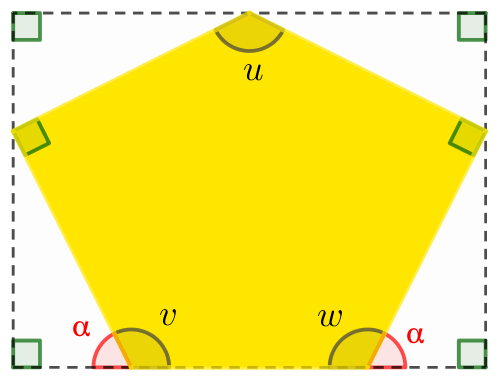
4. Nedenfor ses, at v = w = 180° - 63,4° = 116,6°. Vinkelsummen i en femkant er 540°. Det giver, at u = 540° - 2·90° - 2·116,6° = 126,8°.
   
5. Den regulære femkant som vist nedenunder ikke dække en flade.
   

Svar på opgave 6: Tal-ligevægt

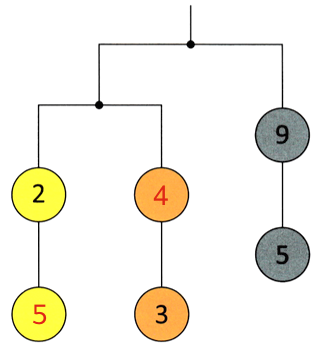
1. Nedenfor er vist den udfyldte tal-ligevægt
   
2. Som i opgave 1 har man, at summen af de gule felter er lig med summen af de orange, og at disse summer hver er halvdelen af summen af de grå felter. De gule felter giver ligningen: 7 + m = (12 + 8)/2 ⇔ m = 3
3. Eftersom der er balance mellem gule og orange felter, så skal summen af de gule felter være 2p + 1. Dette gør, at summen af gule + orange tilsammen giver 4p + 2. Dette skal være lig med summen af tallene i de grå felter, som er 3p + 7. Dette er kun opfyldt for p = 5. Forslag: Gule: 5 og 6. Orange: 10 og 1.
4. Tal-ligevægt 4 er vist nedenunder. Man skal løse følgende to ligninger med to ubekendte:
   2a + 12 = 4 + b og 2a + 12 + 4 + b = b + 18 ⇔
   2a + 8 = b og 2a = 2 ⇔
   2 + 8 = b og a = 1 ⇔
   a = 1 og b = 10