Svar på opgave 1: Køb af smartphone

1. Olivia sparer: 4325 kr. - 3995 kr. = 330 kr.
2. Pris med rabat for Mobilbazaren: 4325 kr. - (4325·0,15 kr.) = 3676,25 kr.
3. Procentsatsen for rabatten kaldes x. Der gælder: 3995 kr. - (3995 kr.)·x = 3676,25 kr. ⇔ x = 0,0798.
   Det vil sige, at procentsatsen for rabatten skal være 8,0 %
4. Samlet pris for Teleboden er: 3995 kr. - (3.995 kr.)·0,05 - 200 kr. = 3595,25 kr..
   Dette skal sammenlignes med pris med rabat i Mobilbazaren, som er 3676,25 kr.
   Det betyder, at Teleboden er billigst

Svar på opgave 2: Skærmstørrelsen på en smartphone

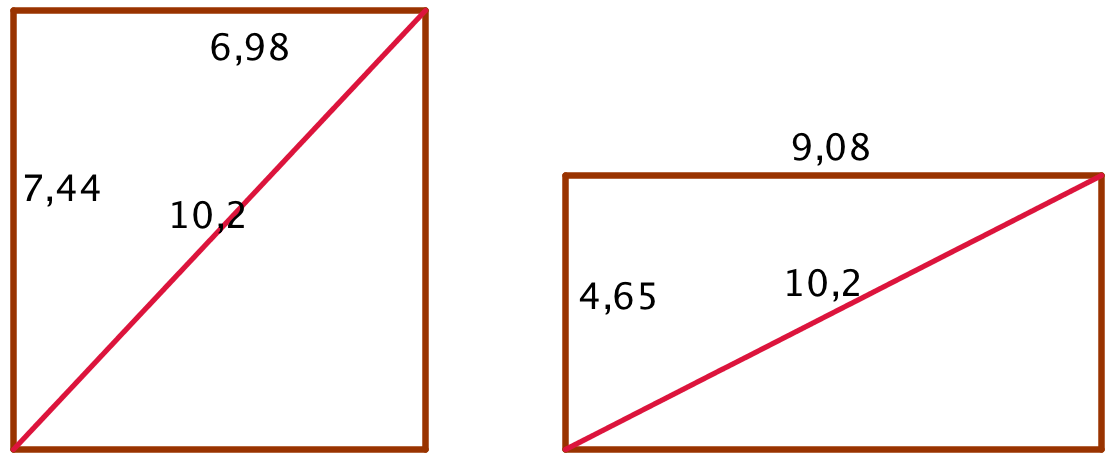
1. Diagonalen er 4·2,54 cm = 10,2 cm
2. To rektangler med diagonalen 10,2.
   
3. Man skal finde den korteste katete, a, i en retvinklet trekant. hvor hypotenusen c = 10,2, den længste katete, b = a·(16/9). Pythagoras' læresætning giver:
   a² + (a·(16/9))² = 10,2² ⇔
   a² = (10,2²)/(1 + (16/9)²) ⇒
   a = √[(10,2²)/(1 + (16/9)²)] ≈ 5.
   Dette viser, at Olivia har ret

Svar på opgave 3: Mobilabonnement

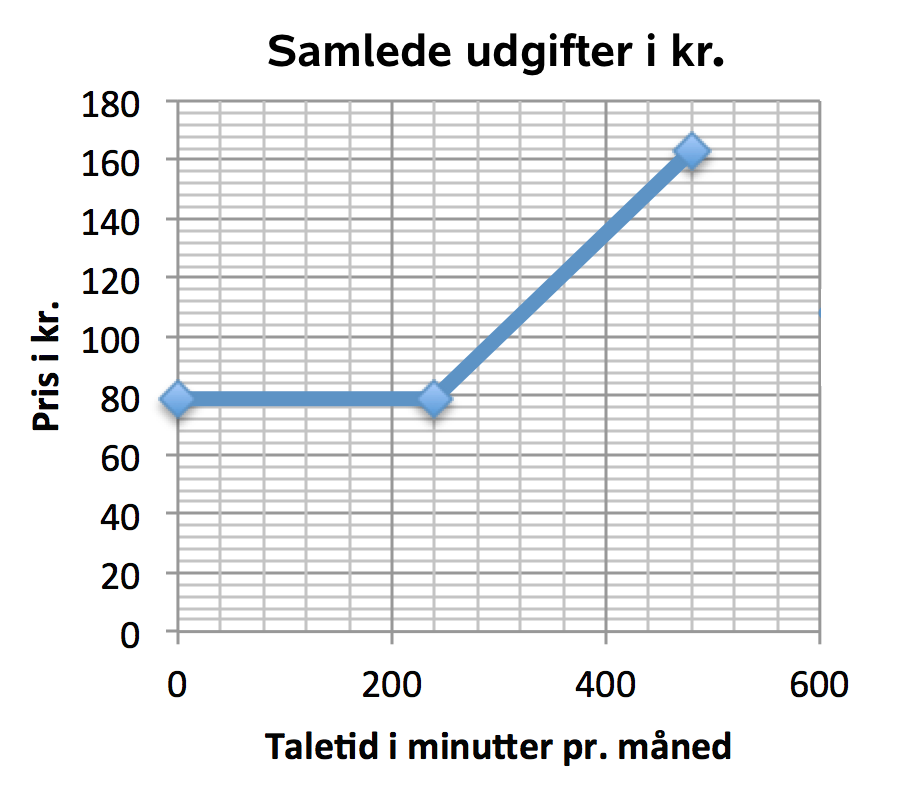
1. Olivia skal betale 49 kr. + 6·79 kr = 523 kr.
2. Regneudtrykket er 49 + n·79 kr.
3. Hun skal betale 79 kr. + (5 t + 20 m - 4 t)·(0,35 kr./m) = 79 kr. + (80 m)·(0,35 kr./m) = 107 kr.
4. Samlede udgifter for abonnement plus taletid tegnet i Excel.
   

Svar på opgave 4: På Facebook

1. Variationsbredden er største tal minus mindste = 60 - 2 = 58
2. Man inddeler antal besøg i grupper og finder antallet i hver gruppe. Grupperne for antal besøg er: 0-10, 11-20, 21-30,...og 51-60. Man får søjlediagrammet:
   
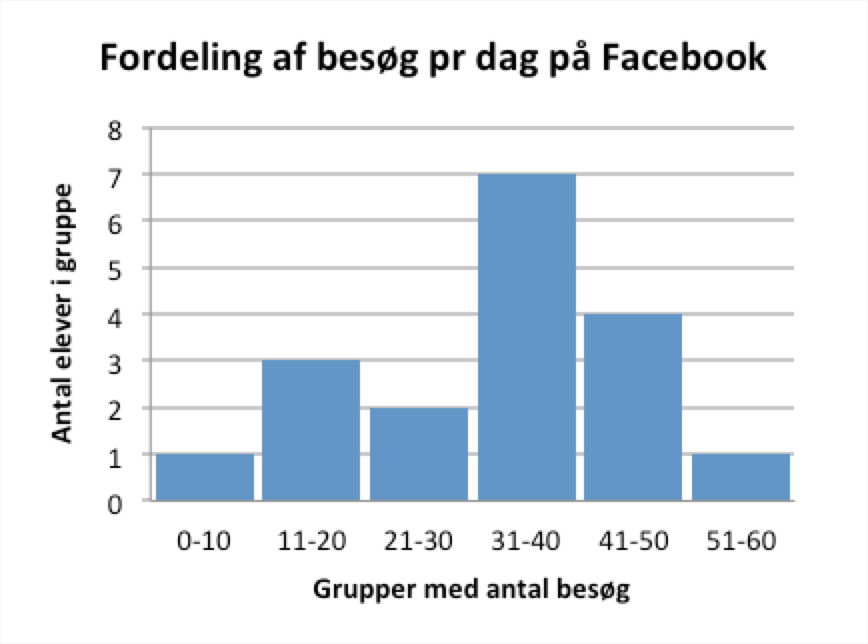
3. Medianen viser, at halvdelen af eleverne foretager færre end eller lig med 40 besøg om dagen på Facebook.
4. Ved den viste inddeling er gruppen, der besøger Facebook mere end 30 gange om dagen, den største. Den udgør 40% af alle elever. Den mindste gruppe er den, der besøger Facebook 6-14 gange om dagen. Den udgør ca. 9 % af eleverne.
5. Man kan sammenligne den del af eleverne, der bruger Facebook mere end 30 gange om dagenn. For Olivias klasse er det 12/18 = 67 %. For resten af eleverne i 6.-9. klasse er det 40 %. Dermed har Olivia ret

Svar på opgave 5: En ydre og to indre cirkler

1. Tegning i Geogebra.
   
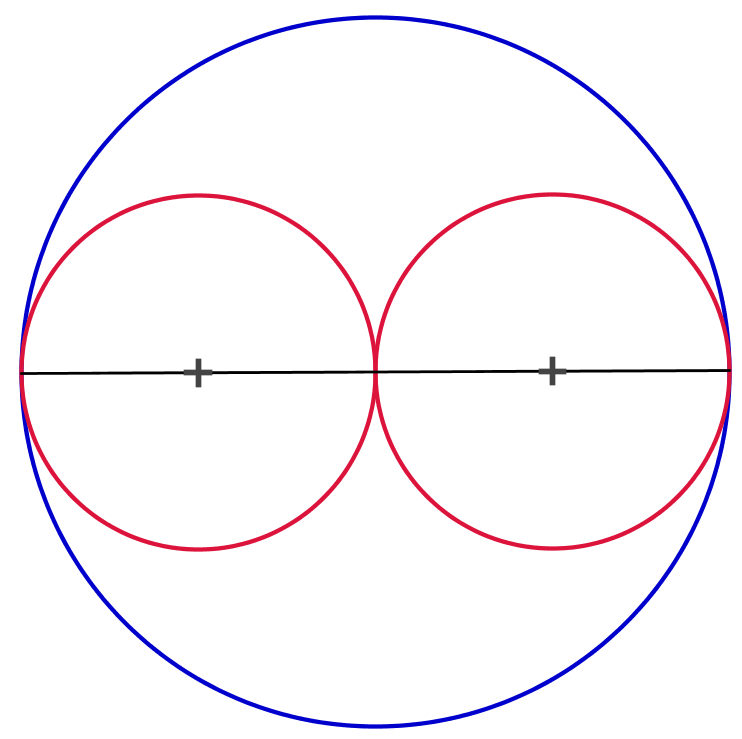
2. Olivia har ret fordi omkredsen af den ydre cirkel er 12·π. Hver af de indre cirkler har omkredsen 6·π, så summen af deres omkredse er derfor også 12·π
3. Den store cirkel har arealet π.6² = 36·π. Hver af de små cirkler har arealet π·3² = 9·π. Tilsammen er deres areal 18·π hvlket er halvdelen af den store cirkels areal.
4. Et eksempel, hvor det ikke gælder: Radius for den store cirkel sættes til 6. De to indre cirkler radier sættes til 4 og 2. For arealerne gælder:
   Areal af stor cirkel: π·6² = π·36.
   Sum af areal af små cirkler: π·(4² + 2²) = π·20.
   Som det ses, er den store cirkels areal ikke dobbelt så stort som summen af de små cirklers arealer.
5. Man får, at omkredsen af den store cirkel er d·π. Omkredserne af de to små cirkler er til sammen: π·e + π·(d - e) = π·d. Dermed gælder reglen

Svar på opgave 6: Talfølger i en gangetabel

1. Det næste røde tal er 11·11 = 121
2. Det kan beregnes som 99² = 9801
3. Der er to muligheder, der begge er markeret med gult.
   
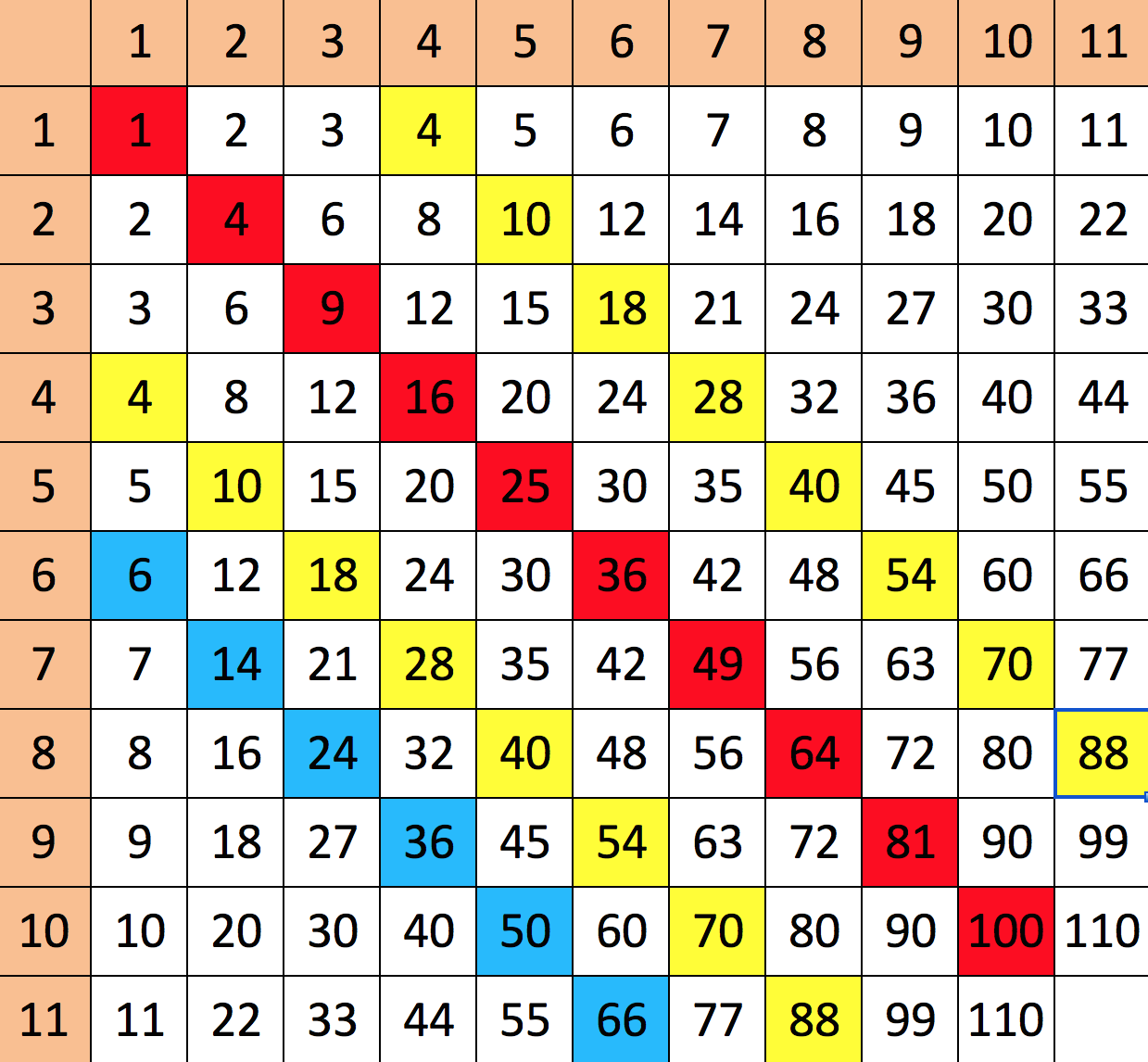
4. Det første tal i den blå talfølge er 1·6 = 6. For at komme til det 9. tal, så skal man lægge 8 til hver: (1 + 8)·(6 + 8)´= 9·14 = 126
5. De blå tal følger systemet: 1·6, 2·7, 3·8, 4·9, 5·10, 6·11...Det vil sige, at første faktor er n, mens anden faktor er n + 5. Regneudtrykket er derfor: n·(n + 5).