Svar på opgave 1: Esters fritidsjob

1. Hun tjente 2·68,96 kr. = 137,92 kr.
2. Ester arbejde i 4 timer heraf 3 timer over. Det giver en løn på: 4·68,96 kr. + 3·12,38 kr. = 312,98 kr.
3. Antallet af timer, som Ester arbejder kaldes x. Hvis hun arbejder over i halvdelen af sin arbejdstid, så tjener hun: x·68,96 kr./time + 0,5·x·12,38 kr./time = x·75,15 kr./time. Man finder x af ligningen: x·75,15 = 2000 ⇔ x = 2000/75,15 = 26,6. Det vil sige, at hun arbejder 26,6 timer
4. Hun får udbetalt: 2000 kr. - (2000 kr.)·0,08 = (2000 kr.)·0,92 = 1840 kr.
5. Hun skal tjene: 2000/0,92 kr. = 2174 kr.

Svar på opgave 2: Katrine maler

1. Lærredet, når det er inddelt i 9 lige store rektangler.
   
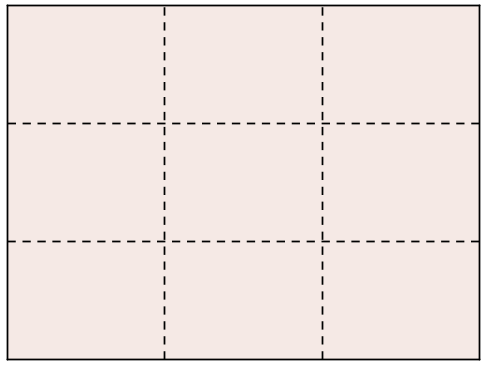
2. l/1,618 er ca. 2/3 af lærredets højde. Det passer med placeringen af horisontlinjen.
3. Længden til horisonten fra underkanten med den første metode er: (50 cm)/1,618 = 30,9 cm. Med den anden metode, får man længden: (2/3)·(50 cm) = 33,3 cm. Forskellen er 33,3 cm - 30,9 cm = 2,4 cm

Svar på opgave 3: Backgammon

1. Sandsynligheden er 6/36 = 1/6. Der er 6 ud af 36 forskellige kast med terningerne, hvor de viser samme antal øjne. Disse er i diagonalen med rødt nedenunder.
   

   	1	2	3	4	5	6
   1	11	12	13	14	15	16
   2	21	22	23	24	25	26
   3	31	32	33	34	35	36
   4	41	42	43	44	45	46
   5	51	52	53	54	55	56
   6	61	62	63	64	65	66

2. Der er 21 forskellige kombinationer. Disse er tallene i diagonalen samt de, som ligger over den i ovenstående tabel.
3. Nedenstående tabel viser forskellen på antal øjne ved de 36 mulige kast. De kombinationer, hvor forskellen er 2 er vist med rødt, og de hvor forskellen er 3 er vist med blåt. Det viser, at sandsynligheden for, at forskellen er 2 = 8/36 = 0,222, og sandsynligheden for at forskellen er 3 er 6/36 = 1/6 = 0,167. Jonathan har derfor ret
   

   	1	2	3	4	5	6
   1	0	1	2	3	4	5
   2	1	0	1	2	3	4
   3	2	1	0	1	2	3
   4	3	2	1	0	1	2
   5	4	3	2	1	0	1
   6	5	4	3	2	1	0

4. Sandsynligheden for at Anna vinder ét spil er 0,5. Sandsynligheden for at hun vinder tre i træk er 0,5·0,5·0,5 = 0,125 = 12,5 %

Svar på opgave 4: Halvmaratonløb

1. Man kan aflæse, at han har løbet i 21 minutter
   
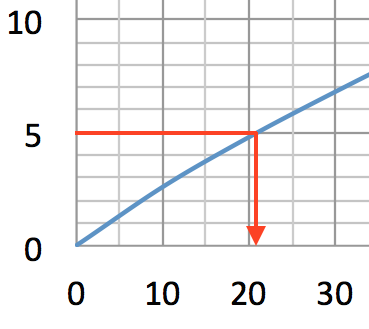
2. Hans tid pr. km er i gennemsnit: (118 min.)/(21.1 km) ≈ 5,6 min./km
3. Det ses af tabellen, at han løber den første halvdel på ca. 50 minutter. Anden halvdel tager 118 min. - 50 min. = 68 min. Dermed tager anden halvdel længst tid
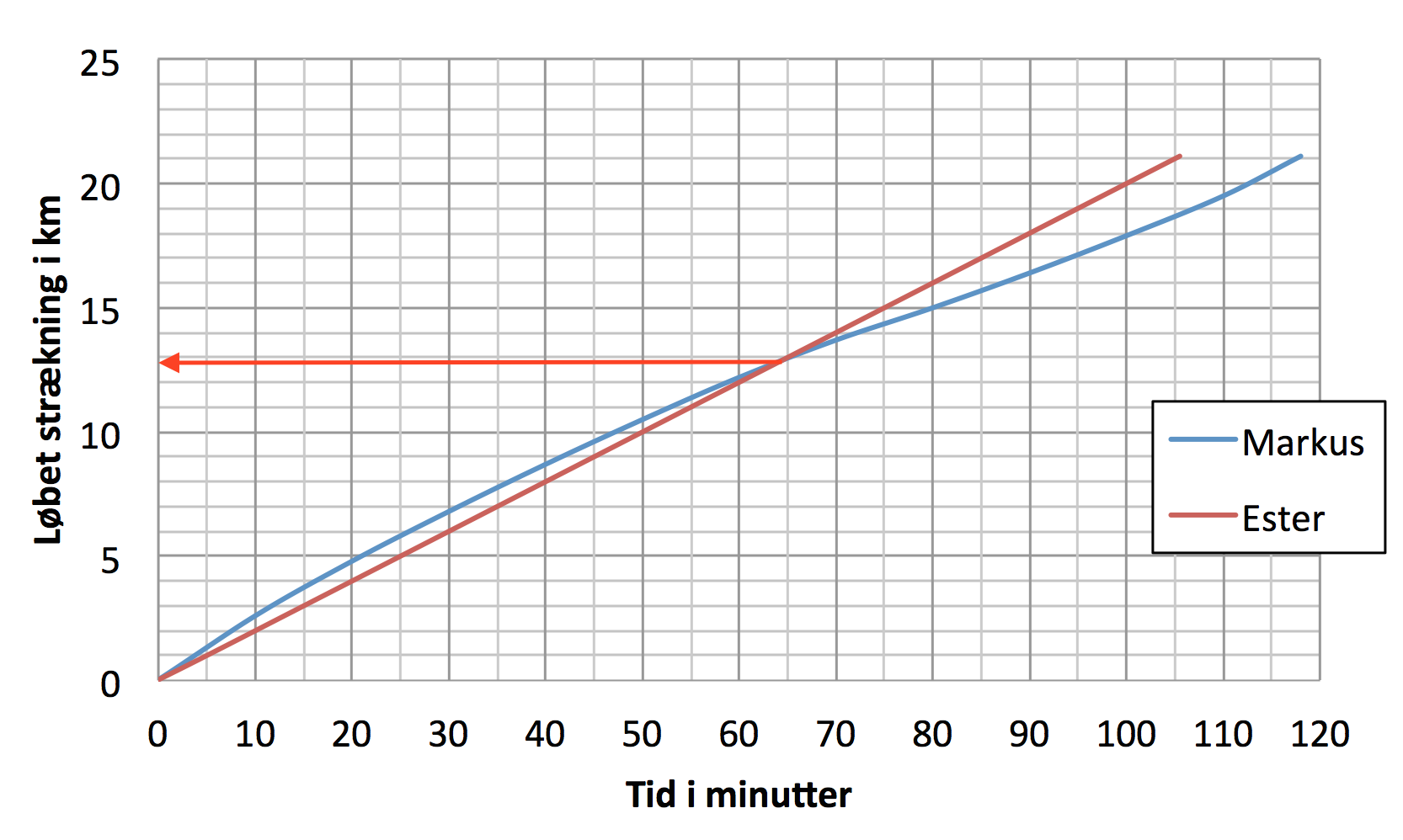
4. Ester gennemførte halvmaratonen på (21,1 km)·(5min./km) = 105,5 min.
5. Der gælder forskriften: y = (1/5)·x, hvor y er tiden i minutter, og x er den tilbagelagte strækning i km.
6. Af kurven ses, at Markus har løbet 12,8 km, da Ester overhaler ham.
   

Svar på opgave 5: Babyloniernes formel for arealet af en firkant

1. Arealet i følge babyloniernes formel er ((3,5 + 3,5)·(6,5 + 6,5)/4) cm² = (7·13/4) cm² = 22,75 cm².
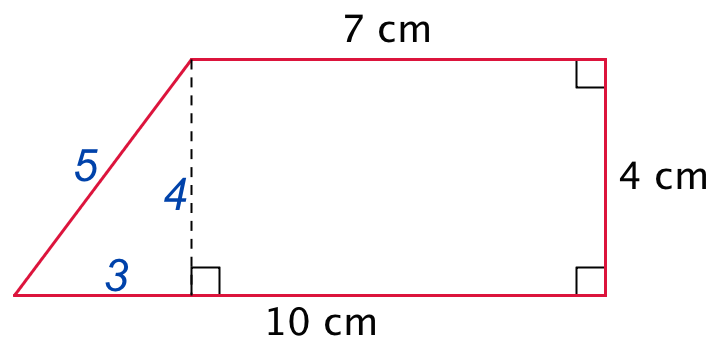
2. Det rigtige areal af trapezen er 4·(7 + 10)/2 cm² = 34 cm². Den skrå side i trapezet er hypotenusen i en retvinklet 3,4,5-trekant og dermed 5 cm² som vist nedenunder.
   Arealet bliver i følge babyloniernes formel: (7 + 10)·(5 + 4)/4 cm² = (17·9/4) cm² = 38,25 cm². Forskellen er (38,25 - 34) cm² = 4,25 cm².
   
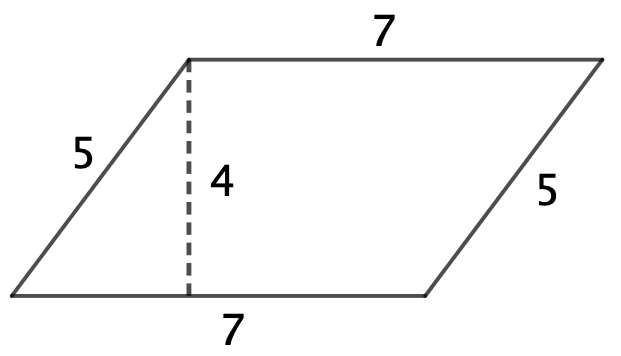
3. Den gælder ikke for alle parallelogrammer. Nedenfor er vist et modeksempel med et parallelogram, som har siderne 5 og 7 samt højden 4. Arealet af parallogrammet er 4·7 = 28. Med babylonernes formel får man arealet: (a+c)·(b+d)/4 = (2·5)·(2·7)/4 = 35. Dermed gælder den ikke altid.
   
4. For kvadratet gælder, at a = b = c = d = s. Det giver følgende med babyloniernes formel: (s + s)(s + s)/4 = (2s)·(2s)/4 = 4s²/4 = s²

Svar på opgave 6: Sumpyramider

1. Sumpyramide 1 bliver:
   
2. Sumpyramide 2 bliver:
   
3. Sumpyramide 3 bliver:
   
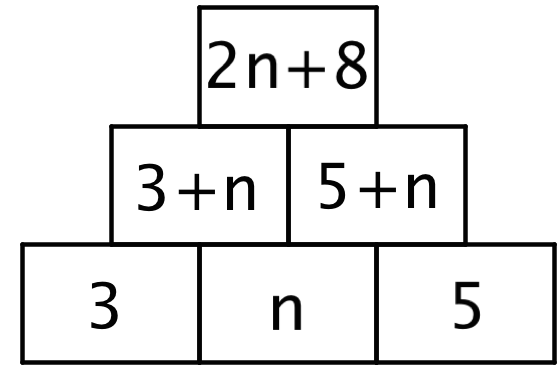
4. Ligningen bliver: 7 + p + p + 4 = 29 ⇔ p = (29 - 11)/2 ⇔ p = 9